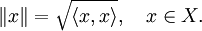- Норма вектора
-
Норма — структура длины векторов на линейном пространстве.
Норма в векторном линейном пространстве
 над полем вещественных или комплексных чисел есть функция
над полем вещественных или комплексных чисел есть функция 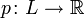 , удовлетворяющая следующим условиям (аксиомы нормы):
, удовлетворяющая следующим условиям (аксиомы нормы):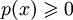 , причём p(x) = 0 только при
, причём p(x) = 0 только при 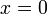 ;
;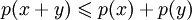 для всех
для всех 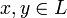 (неравенство треугольника);
(неравенство треугольника);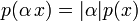 для любого скаляра α.
для любого скаляра α.
Норма
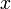 обычно обозначается
обычно обозначается 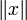 . Линейное пространство с нормой называется нормированным пространством, а условия (1-3) — также аксиомами нормированного пространства.
. Линейное пространство с нормой называется нормированным пространством, а условия (1-3) — также аксиомами нормированного пространства.Аксиома 2 обеспечивает выпуклость шаров
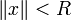 , аксиома 3 — кроме прочего, их центральную симметрию.
, аксиома 3 — кроме прочего, их центральную симметрию.Любой ненулевой вектор (в частности функцию) конечной нормы можно нормировать, поделив его на значение его нормы (после чего он станет нормированным). Также, нередко применяется выражение «нормированный на», подразумевающее, что норма объекта равна в этом случае не единице, а другой определенной величине. Например, иногда говорят о нормировании на дельта-функцию, когда речь идет о нормировании базиса функций, нумерованного непрерывным параметром.
Содержание
Примеры норм в линейных пространствах
- Любое предгильбертово пространство можно считать нормированным, так как скалярное произведение порождает естественную норму
- Гёльдеровы нормы n-мерных векторов (семейство):
![\|x\|_p = \sqrt[p]{\sum_{i} |x_i|^p}](/pictures/wiki/files/99/c6b6a0c35fbd3b375053797441222d9d.png) ,
,
где
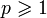 (обычно подразумевается, что это натуральное число). В частности:
(обычно подразумевается, что это натуральное число). В частности:-
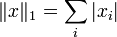
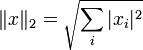 (евклидова норма),
(евклидова норма),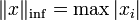 (это предельный случай
(это предельный случай 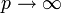 ).
).
- Нормы функций в C[0,1] — пространстве вещественных (или комплексных) непрерывных функций на отрезке [0,1]:
![\|f\|_{C[0,1]} = \max_{x \in [0,1]}|f(x)|](/pictures/wiki/files/100/d3abee88295924c1016de4b32abcf2eb.png) — в смысле этой нормы пространство C[0,1] непрерывных на отрезке функций образует полное линейное пространство. Этого нельзя сказать о следующих двух примерах нормы на этом пространстве, тем не менее, законных:
— в смысле этой нормы пространство C[0,1] непрерывных на отрезке функций образует полное линейное пространство. Этого нельзя сказать о следующих двух примерах нормы на этом пространстве, тем не менее, законных: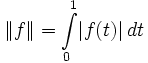
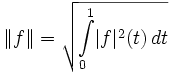
- Аналогично можно ввести нормы для конечномерных векторных функций конечномерных векторных аргументов, заменив
 на
на  , а интегрирование по отрезку интегрированием по области (максимум же на отрезке - в соответствующем случае - максимумом на области).
, а интегрирование по отрезку интегрированием по области (максимум же на отрезке - в соответствующем случае - максимумом на области).
Топология пространства и норма
Норма задаёт на пространстве метрику (в смысле - функцию расстояния метрического пространства), порождая таким образом метрическое пространство, а значит топологию, базой которой являются всевозможные открытые шары, то есть множества вида
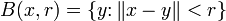 . Понятия сходимости, определённой на языке теоретико-множественной топологии в такой топологии и определённой на языке нормы, при этом совпадают.
. Понятия сходимости, определённой на языке теоретико-множественной топологии в такой топологии и определённой на языке нормы, при этом совпадают.Эквивалентность норм
Две нормы p и q на пространстве L называются эквивалентными, если существует две положительные константы C1 и C2 такие, что для любого
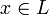 выполняется
выполняется 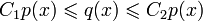 . Эквивалентные нормы задают на пространстве одинаковую топологию. В конечномерном пространстве все нормы эквивалентны.
. Эквивалентные нормы задают на пространстве одинаковую топологию. В конечномерном пространстве все нормы эквивалентны.Операторная норма
Норма оператора A — число, которое определяется, как:
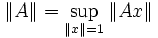 ,
,
- где A — оператор, действующий из нормированного пространства L в нормированное пространство K.
- Свойства операторных норм:
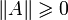 , причём
, причём 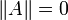 только при A = 0;
только при A = 0;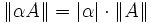 , где
, где 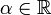 ;
;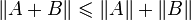 ;
;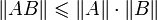 .
.
Матричная норма
Нормой матрицы A называется действительное число
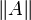 , удовлетворяющее первым трём из следующих условий:
, удовлетворяющее первым трём из следующих условий: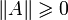 , причём
, причём 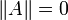 только при
только при 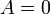 ;
;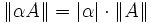 , где
, где 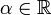 ;
;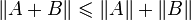 ;
;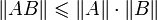 .
.
Если выполняется также и четвёртое свойство, норма называется мультипликативной. Матричная норма, составленная как операторная, называется подчинённой по отношению к норме, использованной в пространствах векторов. Очевидно, что все подчинённые матричные нормы мультипликативны. Немультипликативные нормы для матриц являются простыми нормами, заданными в линейных пространствах матриц.
Некоторые виды матричных норм
- m-норма:
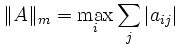
- l-норма:
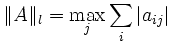
- Норма Фробениуса:
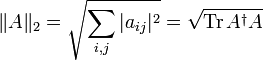 .
.
- Здесь
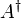 — сопряжённая к A матрица, Tr — след матрицы.
— сопряжённая к A матрица, Tr — след матрицы.
- p-норма (p > 0):
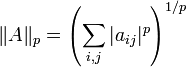
- Сингулярная норма (подчинена евклидовой норме векторов):
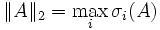 .
.
- Здесь σi(A) — i-ое собственное число матрицы A.
См. также
Wikimedia Foundation. 2010.