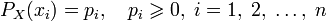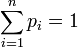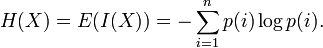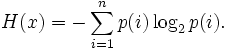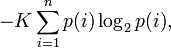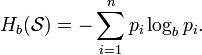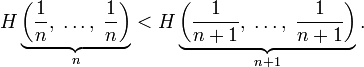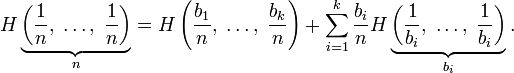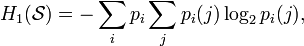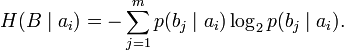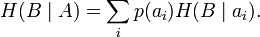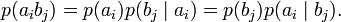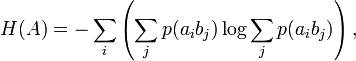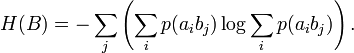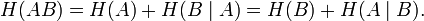- Энтропия (теория информации)
-
Энтропи́я (информационная) — мера хаотичности информации, неопределённость появления какого-либо символа первичного алфавита. При отсутствии информационных потерь численно равна количеству информации на символ передаваемого сообщения.
Например, в последовательности букв, составляющих какое-либо предложение на русском языке, разные буквы появляются с разной частотой, поэтому неопределённость появления для некоторых букв меньше, чем для других. Если же учесть, что некоторые сочетания букв (в этом случае говорят об энтропии n-ого порядка, см. ниже) встречаются очень редко, то неопределённость ещё более уменьшается.
Для иллюстрации понятия информационной энтропии можно также прибегнуть к примеру из области термодинамической энтропии, получившему название демона Максвелла. Концепции информации и энтропии имеют глубокие связи друг с другом, но, несмотря на это, разработка теорий в статистической механике и теории информации заняла много лет, чтобы сделать их соответствующими друг другу.
Содержание
Формальные определения
Определение с помощью собственной информации[1] Также можно определить энтропию случайной величины, введя предварительно понятия распределения случайной величины X, имеющей конечное число значений:
- I(X) = − logPX(X).
Тогда энтропия будет определяться как:
От основания логарифма зависит единица измерения информации и энтропии: бит, нат или хартли.
Информационная энтропия для независимых случайных событий x с n возможными состояниями (от 1 до n) рассчитывается по формуле:
Эта величина также называется средней энтропией сообщения. Величина
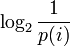 называется частной энтропией, характеризующей только i-e состояние.
называется частной энтропией, характеризующей только i-e состояние.Таким образом, энтропия события x является суммой с противоположным знаком всех произведений относительных частот появления события i, умноженных на их же двоичные логарифмы (основание 2 выбрано только для удобства работы с информацией, представленной в двоичной форме). Это определение для дискретных случайных событий можно расширить для функции распределения вероятностей.
Шеннон предположил, что прирост информации равен утраченной неопределённости, и задал требования к её измерению:
- мера должна быть непрерывной; то есть изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение функции;
- в случае, когда все варианты (буквы в приведённом примере) равновероятны, увеличение количества вариантов (букв) должно всегда увеличивать значение функции;
- должна быть возможность сделать выбор (в нашем примере букв) в два шага, в которых значение функции конечного результата должно являться суммой функций промежуточных результатов.
Шеннон показал, что единственная функция, удовлетворяющая этим требованиям, имеет вид:
где K — константа (и в действительности нужна только для выбора единиц измерения).
Шеннон определил, что измерение энтропии (
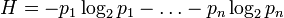 ), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надёжной передачи информации в виде закодированных двоичных чисел. Для вывода формулы Шеннона необходимо вычислить математическое ожидание «количества информации», содержащегося в цифре из источника информации. Мера энтропии Шеннона выражает неуверенность реализации случайной переменной. Таким образом, энтропия является разницей между информацией, содержащейся в сообщении, и той частью информации, которая точно известна (или хорошо предсказуема) в сообщении. Примером этого является избыточность языка — имеются явные статистические закономерности в появлении букв, пар последовательных букв, троек и т. д. См.: Цепи Маркова.
), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надёжной передачи информации в виде закодированных двоичных чисел. Для вывода формулы Шеннона необходимо вычислить математическое ожидание «количества информации», содержащегося в цифре из источника информации. Мера энтропии Шеннона выражает неуверенность реализации случайной переменной. Таким образом, энтропия является разницей между информацией, содержащейся в сообщении, и той частью информации, которая точно известна (или хорошо предсказуема) в сообщении. Примером этого является избыточность языка — имеются явные статистические закономерности в появлении букв, пар последовательных букв, троек и т. д. См.: Цепи Маркова.В общем случае b-арная энтропия (где b равно 2, 3, …) источника
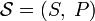 с исходным алфавитом
с исходным алфавитом 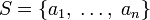 и дискретным распределением вероятности
и дискретным распределением вероятности 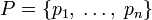 где pi является вероятностью ai (pi = p(ai)) определяется формулой:
где pi является вероятностью ai (pi = p(ai)) определяется формулой:Определение энтропии Шеннона связано с понятием термодинамической энтропии. Больцман и Гиббс проделали большую работу по статистической термодинамике, которая способствовала принятию слова «энтропия» в информационную теорию. Существует связь между термодинамической и информационной энтропией. Например, демон Максвелла также противопоставляет термодинамическую энтропию информации, и получение какого-либо количества информации равно потерянной энтропии.
Альтернативное определение
Другим способом определения функции энтропии H является доказательство, что H однозначно определена (как указано ранее), если и только если H удовлетворяет условиям:
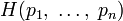 определена и непрерывна для всех
определена и непрерывна для всех 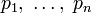 , где
, где ![p_i\in[0,\;1]](/pictures/wiki/files/55/79edfb93a8cac7fb715b01fb439dab36.png) для всех
для всех 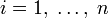 и
и 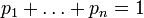 . (Заметьте, что эта функция зависит только от распределения вероятностей, а не от алфавита.)
. (Заметьте, что эта функция зависит только от распределения вероятностей, а не от алфавита.)- Для целых положительных n, должно выполняться следующее неравенство:
- Для целых положительных bi, где
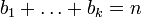 , должно выполняться равенство:
, должно выполняться равенство:
Свойства
Важно помнить, что энтропия является количеством, определённым в контексте вероятностной модели для источника данных. Например, кидание монеты имеет энтропию − 2(0,5log20,5) = 1 бит на одно кидание (при условии его независимости). У источника, который генерирует строку, состоящую только из букв «А», энтропия равна нулю:
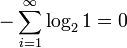 . Так, например, опытным путём можно установить, что энтропия английского текста равна 1,5 бит на символ, что конечно будет варьироваться для разных текстов. Степень энтропии источника данных означает среднее число битов на элемент данных, требуемых для её зашифровки без потери информации, при оптимальном кодировании.
. Так, например, опытным путём можно установить, что энтропия английского текста равна 1,5 бит на символ, что конечно будет варьироваться для разных текстов. Степень энтропии источника данных означает среднее число битов на элемент данных, требуемых для её зашифровки без потери информации, при оптимальном кодировании.- Некоторые биты данных могут не нести информации. Например, структуры данных часто хранят избыточную информацию, или имеют идентичные секции независимо от информации в структуре данных.
- Количество энтропии не всегда выражается целым числом бит.
Математические свойства
- Неотрицательность:
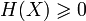 .
. - Ограниченность:
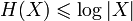 . Равенство, если все элементы из X равновероятны.
. Равенство, если все элементы из X равновероятны. - Если
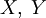 независимы, то H(XY) = H(X) + H(Y).
независимы, то H(XY) = H(X) + H(Y). - Энтропия — выпуклая вверх функция распределения вероятностей элементов.
- Если
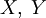 имеют одинаковое распределение вероятностей элементов, то H(X) = H(Y).
имеют одинаковое распределение вероятностей элементов, то H(X) = H(Y).
Эффективность
Исходный алфавит, встречающийся на практике, имеет вероятностное распределение, которое далеко от оптимального. Если исходный алфавит имел n символов, тогда он может быть сравнён с «оптимизированным алфавитом», вероятностное распределение которого однородно. Соотношение энтропии исходного и оптимизированного алфавита — это эффективность исходного алфавита, которая может быть выражена в процентах.
Из этого следует, что эффективность исходного алфавита с n символами может быть определена просто как равная его n-арной энтропии.
Энтропия ограничивает максимально возможное сжатие без потерь (или почти без потерь), которое может быть реализовано при использовании теоретически — типичного набора или, на практике, — кодирования Хаффмана, кодирования Лемпеля — Зива — Велча или арифметического кодирования.
Вариации и обобщения
Условная энтропия
Если следование символов алфавита не независимо (например, во французском языке после буквы «q» почти всегда следует «u», а после слова «передовик» в советских газетах обычно следовало слово «производства» или «труда»), количество информации, которую несёт последовательность таких символов (а следовательно и энтропия) очевидно меньше. Для учёта таких фактов используется условная энтропия.
Условной энтропией первого порядка (аналогично для Марковской модели первого порядка) называется энтропия для алфавита, где известны вероятности появления одной буквы после другой (то есть вероятности двухбуквенных сочетаний):
где i — это состояние, зависящее от предшествующего символа, и pi(j) — это вероятность j, при условии, что i был предыдущим символом.
Так, для русского языка без буквы «ё»
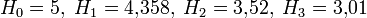 .[2]
.[2]Через частную и общую условные энтропии полностью описываются информационные потери при передаче данных в канале с помехами. Для этого применяются так называемые канальные матрицы. Так, для описания потерь со стороны источника (то есть известен посланный сигнал), рассматривают условную вероятность
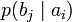 получения приёмником символа bj при условии, что был отправлен символ ai. При этом канальная матрица имеет следующий вид:
получения приёмником символа bj при условии, что был отправлен символ ai. При этом канальная матрица имеет следующий вид:b1 b2 … bj … bm a1 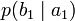
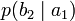
… 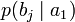
… 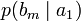
a2 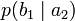
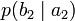
… 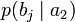
… 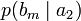
… … … … … … … ai 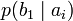
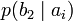
… 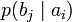
… 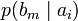
… … … … … … … am 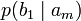
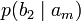
… 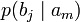
… 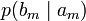
Очевидно, вероятности, расположенные по диагонали описывают вероятность правильного приёма, а сумма всех элементов столбца даст вероятность появления соответствующего символа на стороне приёмника — p(bj). Потери, приходящиеся на передаваемый сигнал ai, описываются через частную условную энтропию:
Для вычисления потерь при передаче всех сигналов используется общая условная энтропия:
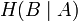 означает энтропию со стороны источника, аналогично рассматривается
означает энтропию со стороны источника, аналогично рассматривается 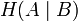 — энтропия со стороны приёмника: вместо
— энтропия со стороны приёмника: вместо 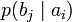 всюду указывается
всюду указывается 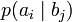 (суммируя элементы строки можно получить p(ai), а элементы диагонали означают вероятность того, что был отправлен именно тот символ, который получен, то есть вероятность правильной передачи).
(суммируя элементы строки можно получить p(ai), а элементы диагонали означают вероятность того, что был отправлен именно тот символ, который получен, то есть вероятность правильной передачи).Взаимная энтропия
Взаимная энтропия, или энтропия объединения, предназначена для расчёта энтропии взаимосвязанных систем (энтропии совместного появления статистически зависимых сообщений) и обозначается H(AB), где A, как всегда, характеризует передатчик, а B — приёмник.
Взаимосвязь переданных и полученных сигналов описывается вероятностями совместных событий p(aibj), и для полного описания характеристик канала требуется только одна матрица:
p(a1b1) p(a1b2) … p(a1bj) … p(a1bm) p(a2b1) p(a2b2) … p(a2bj) … p(a2bm) … … … … … … p(aib1) p(aib2) … p(aibj) … p(aibm) … … … … … … p(amb1) p(amb2) … p(ambj) … p(ambm) Для более общего случая, когда описывается не канал, а просто взаимодействующие системы, матрица необязательно должна быть квадратной. Очевидно, сумма всех элементов столбца с номером j даст p(bj), сумма строки с номером i есть p(ai), а сумма всех элементов матрицы равна 1. Совместная вероятность p(aibj) событий ai и bj вычисляется как произведение исходной и условной вероятности,
Условные вероятности производятся по формуле Байеса. Таким образом имеются все данные для вычисления энтропий источника и приёмника:
Взаимная энтропия вычисляется последовательным суммированием по строкам (или по столбцам) всех вероятностей матрицы, умноженных на их логарифм:
H(AB) = − ∑ ∑ p(aibj)logp(aibj). i j Единица измерения — бит/два символа, это объясняется тем, что взаимная энтропия описывает неопределённость на пару символов — отправленного и полученного. Путём несложных преобразований также получаем
Взаимная энтропия обладает свойством информационной полноты — из неё можно получить все рассматриваемые величины.
История
В 1948 году, исследуя проблему рациональной передачи информации через зашумлённый коммуникационный канал, Клод Шеннон предложил революционный вероятностный подход к пониманию коммуникаций и создал первую, истинно математическую, теорию энтропии. Его сенсационные идеи быстро послужили основой разработки двух основных направлений: теории информации, которая использует понятие вероятности и эргодическую теорию для изучения статистических характеристик данных и коммуникационных систем, и теории кодирования, в которой используются главным образом алгебраические и геометрические инструменты для разработки эффективных кодов.
Понятие энтропии, как меры случайности, введено Шенноном в его статье «A Mathematical Theory of Communication», опубликованной в двух частях в Bell System Technical Journal в 1948 году.
Примечания
- ↑ Габидулин, Э. М., Пилипчук, Н. И. Лекции по теории информации. — М.: МФТИ, 2007. — С. 16. — 214 с. — ISBN 5-7417-0197-3
- ↑ Д. С. Лебедев, В. А. Гармаш. О возможности увеличения скорости передачи телеграфных сообщений. — М.: Электросвязь, 1958. — № 1. — С. 68—69.
См. также
- Собственная информация
- Взаимная информация
- Энтропийное кодирование
- Цепь Маркова
- Термодинамическая энтропия
Ссылки
- Claude E. Shannon. A Mathematical Theory of Communication(англ.)
- С. М. Коротаев. Энтропия и информация — универсальные естественнонаучные понятия
Литература
- Шеннон К. Работы по теории информации и кибернетике. — М.: Изд. иностр. лит., 1963. — 830 с.
- Волькенштейн М. В. Энтропия и информация. — М.: Наука, 1986. — 192 с.
- Цымбал В. П. Теория информации и кодирование. — К.: Выща Школа, 1977. — 288 с.
Wikimedia Foundation. 2010.