ТЕОРИЯ ИНФОРМАЦИИ

ТЕОРИЯ ИНФОРМАЦИИ

-наука о статистич. процессах передачи информации в техн., природных и социальных системах. Осн. понятия Т. <н.- мера кол-ва информации, пропускная способность канала связи, эфф. кодирование сообщений - были введены в 40-х гг. 20 в. К. Шенноном [1 ]. Т. <н. является по существу статистич. теорией связи, или теорией передачи информации, однако общий характер её положений позволяет исследовать также процессы получения, обработки и хранения информации.

Т. и. тесно связана с теорией кодирования, в к-рой рассматриваются общие проблемы установления соответствия между сообщениями и сигналами, представляющими эти сообщения (см. также Кодирование информации), а также с теорией обработки сигналов, в к-рую входит квантование и восстановление квантованных сигналов, а также корреляц. и спектральный анализы сигналов.

Методы Т. и. использовались с разной степенью плодотворности во мн. прикладных областях, включая информатику, языкознание, криптографию, теорию управления, обработку изображений, генетику, психологию, экономику, организацию производства, однако осн. значение они имеют для теории систем связи. Возникновение Т. и. стимулировало также исследования в области теории вероятностей.

Т. и. рассматривает понятие "информации" только с количеств. стороны, безотносительно к её ценности и даже смыслу. При таком подходе страница машинописного текста максимально содержит всегда примерно одинаковое кол-во информации, определяемое только числом знаков и пробелов (т. е. символов) на странице и не зависящее от того, что именно на ней напечатано, включая случай бессмысленного, хаотического набора символов. Для моделирования систем связи такой подход правомерен, поскольку они предназначены для безошибочной передачи по каналу связи информации, представленной любым набором символов. В тех же случаях, когда существен учёт ценности и смысла информации, количеств. подход неприменим. Это обстоятельство налагает существенные ограничения на области возможных приложений Т. и. Неучёт его привёл на ранних этапах развития к переоценке прикладной значи-

Осн. структурная схема системы связи, рассматриваемая в Т. <и., приведена на рис. 1. Информацию в виде сообщений создаёт и с т о ч н и к с о о б щ е н и й. Сообщения представляют собой слова или наборы слов, записанные б у к в а м и нек-рого алфавита. Источниками сообщений могут быть человеческая речь, тексты на любых естеств. или формальных языках, данные систем сбора и обработки информации, а также нек-рые математич. модели -вероятностные процессы, создающие последовательности букв. П е р е д а т ч и к преобразует передаваемое сообщение в сигнал, соответствующий физ. природе к а н а л а с в я з и. Канал связи - это среда для передачи сигнала от передатчика к приёмнику. При прохождении сигнала по каналу на него могут воздействовать п о м е х и, вносящие искажения в значения информац. параметров сигнала. П р и ё м н и к восстанавливает по принятому в общем случае с искажениями сигналу исходное сообщение. Восстановленное сообщение поступает а д р е с а т у - нек-рому лицу или техн. устройству.

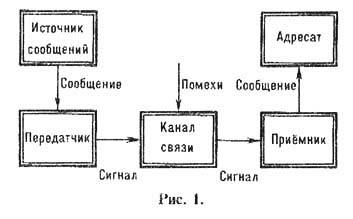
Источники сообщений, рассматриваемые в теории информации, имеют статистич. характер, т. е. появление каждого из возможных сообщений (полный набор к-рых предполагается заранее известным) определяется соответствующей априорной вероятностью. Согласно Шеннону [1 ], считается, что чем больше априорная вероятность данного сообщения, тем меньше неопределённости относительно его действительного появления и, следовательно, тем меньше информации оно несёт. Если вероятность появления сообщения-единица, т. е. его появление достоверно, то неопределённости нет и считается, что сообщение не несёт информации.

Для оценки кол-ва информации в сообщении в Т. и, используется логарифмич. мера, введённая Р. Хартли [2], вероятностная интерпретация к-рой была дана в работах Шеннона [1 ]. Если вероятность появления сообщения x есть p(x), причем 0 <р ( х)<1, то к о л и ч е с т в о и н ф о рм а ц и и I(x), содержащееся в сообщении, определяется ф-лой:

Ф-ла (1) определяет кол-во информации с точностью до основания логарифма, т. е. с точностью до пост. множителя. Как правило, в качестве основания логарифма выбирается число 2и единицей кол-ва информации является б и т, что соответствует используемой в вычислит. технике двоичной системе счисления. При любом основании логарифма I(x)>=0, I(x)=0. при р(х)=1и 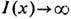при p(x)->0 (рис, 2).

Если x₁. и х₂- сообщения от двух независимых источников с вероятностями появления p(x₁ )и p(x₂), то вероятность их совместного появления r(x₁,x₂)=p(x₁)^.p(x₂) а соответствующее кол-во информации

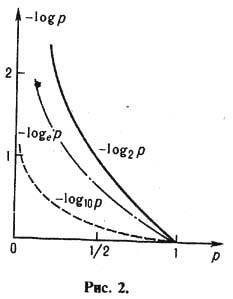
Это аддитивное свойство логарифмич. меры служит основанием для выбора ее в качестве меры кол-ва информации, т. к. соответствует интуитивным представлениям о суммировании кол-ва информации, содержащегося в независимых сообщениях.

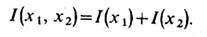
Для сообщений x₁,..., x_n, создаваемых источником с вероятностями p₁...,p_n, причём 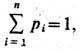Шеннон ввёл ср. меру кол-ва информации усреднением по множеству сообщений

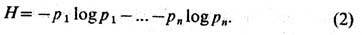
Логарифм здесь, как и в ф-ле (1), обычно берётся по основанию 2, Ф-ция Н, характеризующая информац. свойства источника сообщений, наз. э н т р о п и е й, т. к. по форме она совпадает с энтропией в статистич. физике, характеризующей априорную неопределённость нахождения статистич. системы в состояниях x₁...,x_n, имеющих вероятности p₁ ...,p_n. Очевидна прямая аналогия ф-лы (1) для кол-ва информации в сообщении и ф-лы Больцмана для физ. энтропии S:

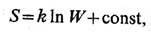
где k- постоянная Больцмана, W-термодинамическая вероятность. В самой Т. и. и её приложениях эта аналогия с физикой не играет, однако, существенной роли.

Если в ф-ле (2) лишь одна из вероятностей равна единице, а остальные-нули, неопределённости в появлении сообщений нет и Н=0. Если сообщения равновероятны: p₁=...=p_n=1/n, и неопределённость в том, какое из них появится, максимальна, то H=log n. Это значение энтропии является максимальным и равно в этом случае кол-ву информации, получаемому от каждого отд. сообщения.

Для источника, создающего два сообщения х₁ и х₂, к-рые можно закодировать в двоичном коде как 0 и 1 соответственно, при вероятностях сообщений p и q=1 -p

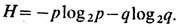
График энтропии для этого случая приведён на рис. 3.

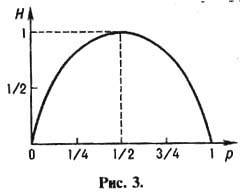
Энтропия максимальная, когда априорная неопределённость максимальна, т. е. при p,q =1/2. При этом Н=1 бит, что соответствует одному двоичному символу (букве), используемому в кодах сообщений.

Если источник создаёт четыре сообщения x₁, x₂, x₃, x₄, то их можно закодировать в двоичном коде так: 00, 01, 10 и 11. При p₁= ... = p₄ =1/4 энтропия максимальна, H=2бит, что соответствует двум двоичным символам, используемым для кодирования сообщений. Вообще для источника, создающего n сообщений, макс. значение энтропии H=log₂n, что соответствует мин. числу двоичных символов в кодовых словах одинаковой длины, образующих р а в н о м е р н ы е к о д ы и необходимых для кодирования n равновероятных сообщений.

Если сообщения не являются равновероятными, то для экономии ср. времени на их передачу по каналу связи предпочтительно использование н е р а в н о м е р н ы х к од о в, образованных более короткими кодовыми словами для более вероятных сообщений и более длинными - для менее вероятных сообщений. Для n кодовых слов, имеющих l₁...,l_n символов, средняя длина слова (сообщения) определяется ф-лой

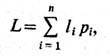
где p_i - вероятности появления соответств. слов (сообщений). Энтропия задаёт ниж. границу для L, т. <е. L>=H. Уменьшение L, т. е. приближение L к H и как следствие уменьшение ср. времени передачи сообщений, возможно за счёт применения процедур э ф ф е к т и в н о г о к о д и р о в ан и я. Эффективность кодирования характеризуется величиной h = H/L, а величина m=1-h наз. и з б ы т о ч н ос т ь ю. Эфф, кодирование, обеспечивающее мин. значение избыточности, можно осуществить с помощью кодов Шеннона, Р. Фано, Д, Хаффмена [1,3] (в случае m = 0 код наз. о п т и м а л ь н ы м).

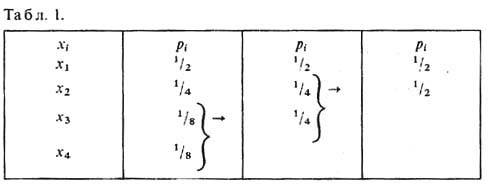
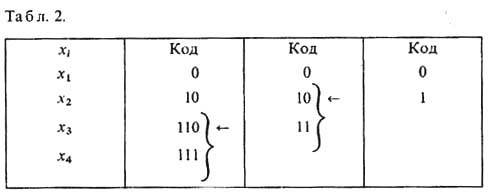
Код Хаффмена строится след. образом. Сообщения (число к-рых конечно) располагаются в таблице в столбец в порядке убывания их вероятностей. Два последних сообщения объединяются в одно с суммарной вероятностью, и далее по тому же правилу строится след. столбец таблицы. Затем в полученном столбце два последних сообщения вновь объединяются в одно с суммарной вероятностью, строится новый столбец таблицы и т. д. Процесс продолжается до тех пор, пока в последнем построенном столбце не останется двух сообщений. Верхнему из них приписывается кодовое слово 0, нижнему - 1. Далее рассматривается предпоследний столбец, в к-ром для объединявшихся сообщений на втором месте кодового слова ставится 0 для верх. сообщения и 1-для нижнего. Если сообщения необъединялись, то они сохраняют кодовые слова предыдущего столбца. Процесс кодирования продолжается до тех пор, пока кодовые слова не будут приписаны всем исходным сообщениям в первом столбце.

Пусть, напр., источник создаёт четыре сообщения x₁, х₂, х₃, х₄ свероятностями p₁ =1/2, р₂=1/4, p₃=р₄= 1/8. Процесс построения кода Хаффмена для этого случая - объединение сообщений и кодирование - показан в табл. 1 и табл. 2 соответственно. Для построенных кодовых слов сообщений 0, 10, 110, 111 ср. длина слова L= 1/2 · 1 + 1/4 · 2 +1/8 · 3 + 1/8 · 3 = 7/4, что равно значению энтропии для рассматриваемого источника: Н= -l/2 log₂1/2- l/4 log₂1/4- l/8 log₂1/8-- l/8 log₂1/8 = 7/4. Избыточность кодирования m =0, эффективность h =1, т. е. построенный код - оптимальный. Использование эфф. кодирования, однако, допустимо только при полной гарантии отсутствия ошибок при кодировании и декодировании сообщений, т. <к. в этом случае ошибка в восстановлении одного сообщения может повлечь появление ошибок при восстановлении многих последующих сообщений.

К наиб. важным проблемам Т. и. относится согласование информац. свойств источника сообщений и канала связи. П р о п у с к н а я с п о с о б н о с т ь канала связи С определяется как макс. кол-во информации, к-рое способен передать канал в единицу времени. Единицей измерения пропускной способности канала связи является 1 бит/с.

Пусть источник создаёт сообщения в виде слов, записываемых буквами алфавита A_m={ а₁ ..., а _т}. При вероятностях появления этих букв p₁,..., р _т на одну букву приходятся в ср. бит информации. О с н о в н а я т е о р е м а Ш е н н о н а д л я к а н а л а с в я з и б е з ш у м а формулируется след. образом.

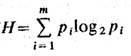
Пусть источник сообщений характеризуется энтропией H (бит/буква), а канал связи имеет пропускную способность С (бит/с). Тогда можно закодировать сообщения так, чтобы передавать символы по каналу связи со ср. скоростью С/H-e (буква/с), где e - сколь угодно малое число. Передавать буквы со ср. скоростью, превышающей С/H, невозможно. Достижение верх. границы для скорости передачи, указываемой теоремой Шеннона, осуществляется за счёт применения процедур эфф. кодирования.

При передаче сигналов по каналам связи на них возможно действие разл. помех, шумов, к-рые могут привести к искажениям восстанавливаемых сообщений. Пусть, как и ранее, источник сообщений создаёт слова, записываемые буквами алфавита A_m = {a₁,..., а _т} при вероятностях их появления р₁..., р _т. Пусть далее вследствие действия помех слова, восстанавливаемые приёмником, оказываются записанными валфавите B_n = {b₁..., b_n}, к-рый, в частности, может совпадать с алфавитом источника, причём вероятности появления букв алфавита В _п равны r₁,..., r_n. Тогда кол-во информации на выходе канала связи относительно его входа, приходящееся на одну передаваемую букву, определяется след. ф-лой:

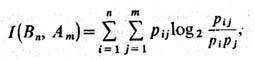
где р _ij(i=l,..., n; j=1,..., m)- вероятности совместного появления букв входного и выходного алфавитов.

Пропускная способность канала связи с шумами С _ш определяется как макс. кол-во информации I(В _n, А _т), к-рое можно передать по каналу связи за 1 с. Максимум находится для всех возможных источников, к-рые могут быть использованы на входе данного канала связи.

Т е о р е м а Ш е н н о н д л я к а н а л а с в я з и с ш у м а м и формулируется след. образом.

Пусть H₁- ср. кол-во информации, создаваемое источником в единицу времени, т, е. производительность источника сообщений, измеряемая в бит/с. Пусть далее С _ш - пропускная способность канала с шумом, тоже измеряемая в бит/с. Тогда если Н ₁ =<С _ш, то такой системы кодирования не существует.

Пропускная способность канала с шумом существенно зависит от действующих на сигналы помех. Рассмотрим двоичный симметричный канал, передающий двоичные буквы 0 и 1 с вероятностью правильной передачи e и искажающий их с вероятностью d =1 - e. Пропускная способность такого канала при передаче одной буквы в секунду определяется ф-лой

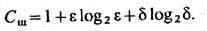
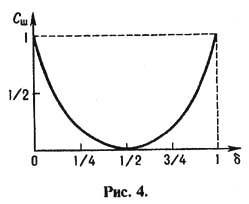
График зависимости С _ш от d приведён на рис. 4. Если e = d = 1/2, т. <е. если вероятность правильной передачи буквы равна вероятности её искажения, то пропускная способность канала с шумом С _ш = 0.

Теорема Шеннона для канала с шумом не указывает конкретного способа борьбы с помехами. Простейший способ борьбы с помехами, состоящий в многократном повторении сообщений, неэффективен, т. к. требует больших затрат времени на передачу. Большую эффективность обеспечивает применение кодов, позволяющих обнаруживать и исправлять ошибки передачи. П о м е х оу с т о й ч и в о с т ь кодирования при этом обеспечивается спец, введением избыточности, т, е, введением в сообщение добавочных символов, к-рые используются для обнаружения и исправления ошибок в принятом сообщении. К числу кодов, обнаруживающих и исправляющих ошибки, относятся к о д ы Х э м м и н г а (см. Кодирование информации).

Лит.:1) Шеннон К., Работы по теории информации и кибернетике, пер. с англ., М., 1963; 2} Хартли Р., Передача информации, [пер. с англ.], в сб.: Теория информации и ее приложения, М., 1959; 3) Стратонович Р. Л., Теория информации, М., 1975; 4) Поплавский Р. П., Термодинамика информационных процессов, М., 1981; 5) Николис Д. С., Динамика иерархических систем, пер. с англ., М., 1989. В, И. Капалин.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.