Кодирование Хаффмана

Алгоритм Хаффмана (англ. Huffman) — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году доктором Массачусетского технологического института Дэвидом Хаффманом. В настоящее время используется во многих программах сжатия данных.

В отличие от алгоритма Шеннона — Фано, алгоритм Хаффмана остаётся всегда оптимальным и для вторичных алфавитов m₂ с более чем двумя символами.

Этот метод кодирования состоит из двух основных этапов:

1. Построение оптимального кодового дерева.
2. Построение отображения код-символ на основе построенного дерева.

Алгоритм

1. Подсчитываются вероятности появления символов первичного алфавита в исходном тексте (если они не заданы заранее)
2. Символы первичного алфавита m₁ выписывают в порядке убывания вероятностей.
3. Последние n₀ символов объединяют в новый символ, вероятность которого равна суммарной вероятности этих символов, удаляют эти символы и вставляют новый символ в список остальных на соответствующее место (по вероятности). n₀ вычисляется из системы:
   $\left\{\begin{matrix} 2 \le n_0 \le m_2 \\ n_0 = m_1 - a(m_2-1) \end{matrix}\right.$,
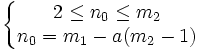   где a — целое число, m₁ и m₂ — мощность первичного и вторичного алфавита соответственно.
4. Последние m₂ символов снова объединяют в один и вставляют его в соответствующей позиции, предварительно удалив символы, вошедшие в объединение.
5. Предыдущий шаг повторяют до тех пор, пока сумма всех m₂ символов не станет равной 1.

Этот процесс можно представить как построение дерева, корень которого — символ с вероятностью 1, получившийся при объединении символов из последнего шага, его m₂ потомков — символы из предыдущего шага и т. д.

Каждые m₂ элементов, стоящих на одном уровне, нумеруются от 0 до m₂-1. Коды получаются из путей (от первого потомка корня и до листка). При декодировании можно использовать то же самое дерево, считывается по одной цифре и делается шаг по дереву, пока не достигается лист — тогда выводится символ, стоящий в листе и производится возврат в корень.

Построение дерева Хаффмана

Бинарное дерево, соответствующее коду Хаффмана, называют деревом Хаффмана.

Задача построения кода Хаффмана равносильна задаче построения соответствующего ему дерева.

Общая схема построения дерева Хаффмана:

1. Составим список кодируемых символов (при этом будем рассматривать каждый символ как одноэлементное бинарное дерево, вес которого равен весу символа).
2. Из списка выберем 2 узла с наименьшим весом (под весом можно понимать частоту использования символа — чем чаще используется, тем больше весит).
3. Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов.
4. Добавим сформированный узел к списку.
5. Если в списке больше одного узла, то повторить 2-5.

Пример реализации

Пример реализации алгоритма Хаффмана на языке

// скомпилируйте и введите java HuffmanTest
class Tree {
   public Tree child0;       // потомки "0" и "1"
   public Tree child1;
   public boolean leaf;      // признак листового дерева
   public int character;     // входной символ
   public int weight;        // вес этого символа
 
   public Tree() {}
 
   public Tree(int character, int weight, boolean leaf) {
     this.leaf = leaf;
     this.character = character;
     this.weight = weight;
   }
 
/*  Обход дерева с генерацией кодов
    1. "Распечатать" листовое дерево и записать код Хаффмана в массив
    2. Рекурсивно обойти левое поддерево (с генерированием кода).
    3. Рекурсивно обойти правое поддерево.
*/
   public void traverse(String code, Huffman h) {
      if (leaf) {
         System.out.println((char)character +"  "+ weight +"  "+ code);
         h.code[character] = code;
      }
      if ( child0 != null) child0.traverse(code + "0", h);
      if ( child1 != null) child1.traverse(code + "1", h);
   }
}
 
class Huffman {
   public static final int ALPHABETSIZE = 256;
   Tree[] tree   = new Tree[ALPHABETSIZE];          // рабочий массив деревьев
   int weights[] = new int[ALPHABETSIZE];           // веса символов
   public String[] code = new String[ALPHABETSIZE]; // коды Хаффмана
 
   private int getLowestTree(int used) {       // ищем самое "легкое" дерево
      int min=0;
      for (int i=1; i<used; i++)
         if (tree[i].weight < tree[min].weight ) min = i;
      return min;
   }
 
   public void growTree( int[] data ) {    // растим дерево
      for (int i=0; i<data.length; i++)    // считаем веса символов
          weights[data[i]]++;
                                   //  заполняем массив из "листовых" деревьев
      int used = 0;                //  с использованными символами
      for (int c=0; c < ALPHABETSIZE; c++) {
         int w = weights[c];
         if (w != 0) tree[used++] = new Tree(c, w, true);
      }
      while (used > 1) {                    // парами сливаем легкие ветки 
         int min = getLowestTree( used );   // ищем 1 ветку
         int weight0 = tree[min].weight;
         Tree temp = new Tree();            // создаем новое дерево
         temp.child0 = tree[min];           // и прививаем 1 ветку
         tree[min] = tree[--used];          // на место 1 ветки кладем
                                            // последнее дерево в списке
         min = getLowestTree( used );               // ищем 2 ветку и
         temp.child1 = tree[min];                   // прививаем ее к нов.дер.
         temp.weight = weight0 + tree[min].weight;  // считаем вес нов.дер.
         tree[min] = temp;                  // нов.дер. кладем на место 2 ветки
      }                                     // все! осталось 1 дерево Хаффмана
   }
 
   public void makeCode() {            // запускаем вычисление кодов Хаффмана
      tree[0].traverse( "", this);
   }
 
   public String coder( int[] data ) { // кодирует данные строкой из 1 и 0
      String str = "";
      for (int i=0; i<data.length; i++) str += code[data[i]];
      return str;
   }
 
   public String decoder(String data) {
      String str="";                  // проверяем в цикле данные на вхождение
      int l = 0;                      // кода, если да, то отбрасываем его ...
      while(data.length() > 0){
        for (int c=0; c < ALPHABETSIZE; c++) {
           if (weights[c]>0 && data.startsWith(code[c])){
              data = data.substring(code[c].length(), data.length());
              str += (char)c;
           }
        }
      }
      return str;
   }
}
 
public class HuffmanTest {                      // тест и демонстрация
   public static void main(String[] args) {
      Huffman h = new Huffman();
      String str = "to be or not to be?";       // входные данные
      int data[] = new int[str.length()];       // преобразуем в массив
      for (int i=0; i<str.length(); i++) data[i] = str.charAt(i); 
      h.growTree( data );                       // растим дерево
      h.makeCode();                             // находим коды
      str = h.coder(data);
      System.out.println(str);
      System.out.println(h.decoder(str));
   }
}

Пример реализации алгоритма Хаффмана на языке Delphi

(* Denis Lemeshko (mailto: skilfulfox {at} gmail {dot} com, www: http://gog.lds.lg.ua/) *)
 
unit CHuffman;
 
interface
 
uses
  SysUtils, Classes, Dialogs;
 
const
  ALPHABETSIZE = 256;
 
type
  TTree = class;
  THuffman = class;
 
  TTree = class(TObject)
  private
    fchild0 : TTree;      // потомки "0" и "1"
    fchild1 : TTree;
    fleaf : Boolean;      // признак листового дерева
    fcharacter : Integer; // входной символ
    fweight : Integer;    // вес этого символа
  public
    procedure Tree(character, weight : integer; leaf : boolean);
    procedure traverse(code : string; h : THuffman);
    property child0 : TTree read fchild0 write fchild0;
    property child1 : TTree read fchild1 write fchild1;
    property leaf : Boolean read fleaf write fleaf;
    property character : Integer read fcharacter write fcharacter;
    property weight : Integer read fweight write fweight;
  end;
 
  THuffman = class(TObject)
  private
    // поля :)
    fweights : array [0..ALPHABETSIZE-1] of Integer;// веса символов
    fcode : array [0..ALPHABETSIZE-1] of String;// коды Хаффмана
    ftree : array [0..ALPHABETSIZE-1] of TTree;// рабочий массив деревьев
    // методы доступа к массиву :)
    function GetCodeValue(Index: Integer): String;
    function GetTreeValue(Index: Integer): TTree;
    function GetWeightValue(Index: Integer): Integer;
    procedure SetCodeValue(Index: Integer; const Value: String);
    procedure SetTreeValue(Index: Integer; const Value: TTree);
    procedure SetWeightValue(Index: Integer; const Value: Integer);
  public
    // методы :)
    procedure makeCode;
    procedure growTree(var data : array of Integer);
    function getLowestTree(used : integer) : integer;
    function coder(var data : array of integer) : string;
    function decoder(data : string) : string;
    // свойства :)
    property weights[Index: Integer] : Integer read GetWeightValue write SetWeightValue;
    property code[Index: Integer] : String read GetCodeValue write SetCodeValue;
    property tree[Index: Integer] : TTree read GetTreeValue write SetTreeValue;
  end;
 
var
  Huffman : THuffman;
 
implementation
 
{ TTree }
 
procedure TTree.Tree(character, weight: integer; leaf: boolean);
begin
  fleaf := leaf;
  fcharacter := character;
  fweight := weight;
end;
 
(*  Обход дерева с генерацией кодов
    1. "Распечатать" листовое дерево и записать код Хаффмана в массив
    2. Рекурсивно обойти левое поддерево (с генерированием кода).
    3. Рекурсивно обойти правое поддерево. *)
procedure TTree.traverse(code: String; h: THuffman);
begin
  if leaf then
  begin
    h.code[Ord(character)] := code;
    ShowMessage('Символ: ' + Chr(character) +'  '+'Вес: '+IntToStr(weight) +'  '+'Двоичный код: '+ code);
  end;
  if child0 <> nil then child0.traverse(code + '0', h);
  if child1 <> nil then child1.traverse(code + '1', h);
end;
 
{ THuffman }
 
(* ищем самое "легкое" дерево *)
function THuffman.getLowestTree(used: integer): integer;
var
  min, i : Integer;
begin
  min := 0;
  for i:=1 to used-1 do if tree[i].weight < tree[min].weight then min := i;
  Result := min;
end;
 
(* кодирует данные строкой из 1 и 0 *)
function THuffman.coder(var data: array of Integer): String;
var
  str : String;
  i : Integer;
begin
  str := '';
  for i:=0 to High(data) do str := str + code[data[i]];
  Result := str;
end;
 
function THuffman.decoder(data : string): string;
var
  str : String;
  c : Integer;
begin
  str := '';
  while(length(data) > 0) do
  begin
    for c:=0 to ALPHABETSIZE-1 do
    if (weights[c] > 0) AND (code[c] = copy(data, 1, length(code[c]))) then
    begin
      data := copy(data, length(code[c])+1, length(data));
      str := str + chr(c) + ' - ' + code[c] + #13;
    end;
  end;
  Result := str;
end;
 
(* растим дерево *)
procedure THuffman.growTree(var data: array of Integer);
var
  i, c, w, min, used, weight0 : Integer;
  temp : TTree;
begin
  for i:=0 to ALPHABETSIZE-1 do weights[i] := 0;
  for i:=0 to High(data) do weights[data[i]] := weights[data[i]] + 1; // считаем веса символов
  //  заполняем массив из "листовых" деревьев
  //  с использованными символами
  used := 0;
  for c:=0 to ALPHABETSIZE-1 do
  begin
    w := weights[c];
    if w <> 0 then
    begin
      inc(used);
      tree[used-1] := TTree.Create;
      tree[used-1].Tree(c, w, true);
    end;
  end;
  while used > 1 do                             // парами сливаем легкие ветки
  begin
    min := getLowestTree(used);                 // ищем 1 ветку
    weight0 := tree[min].weight;
    temp := TTree.Create;                       // создаем новое дерево
    temp.child0 := tree[min];                   // и прививаем 1 ветку
    dec(used);
    tree[min] := tree[used];                    // на место 1 ветки кладем
                                                // последнее дерево в списке
    min := getLowestTree(used);                 // ищем 2 ветку и
    temp.child1 := tree[min];                   // прививаем ее к нов.дер.
    temp.weight := weight0 + tree[min].weight;  // считаем вес нов.дер.
    tree[min] := temp;                          // нов.дер. кладем на место 2 ветки
  end;                                          // все! осталось 1 дерево Хаффмана
end;
 
(* запускаем вычисление кодов Хаффмана *)
procedure THuffman.makeCode;
begin
  tree[0].traverse('', self);
end;
 
function THuffman.GetCodeValue(Index: Integer): String;
begin
  Result := fcode[Index];
end;
 
function THuffman.GetTreeValue(Index: Integer): TTree;
begin
  Result := ftree[Index];
end;
 
function THuffman.GetWeightValue(Index: Integer): Integer;
begin
  Result := fweights[Index];
end;
 
procedure THuffman.SetCodeValue(Index: Integer; const Value: String);
begin
  fcode[Index] := Value;
end;
 
procedure THuffman.SetTreeValue(Index: Integer; const Value: TTree);
begin
  ftree[Index] := Value;
end;
 
procedure THuffman.SetWeightValue(Index: Integer; const Value: Integer);
begin
  fweights[Index] := Value;
end;
 
end.

Результат работы для строки «to be or not to be?». Выводятся: символ, его вес и двоичный код. Далее закодированная строка и результат декодирования.

e  2  000
?  1  0010
n  1  0011
o  4  01
   5  10
t  3  110
r  1  1110
b  2  1111
11001101111000100111101000110111010110011011110000010
to be or not to be?
-----------------------------------------------------------------------
110 01 10 1111 000 10 01 1110 10 0011 01 110 10 110 01 10 1111 000 0010
t   o     b    e      o  r       n    o  t      t   o     b    e   ?
Итого:
53 бита
19 знаков (с пробелами)
2,79 бит/знак

Соответствующее дерево Хаффмана.

       root
      /    \
     0      1
    / \    / \
  00   o "_"  11
 /  \        /  \
e   001     t   111
    / \         /  \
   ?   n       r    b

Ссылки

• Код Хаффмана
• Визуализатор построения дерева для m₂=2
• Визуализатор кодирования букв русского алфавита
• Сжатие по алгоритму Хаффмана @ algolist.manual.ru
• Кодирование Хаффмана объяснение и 2 варианта кодекса в C++
• Визуализатор кодирования и построения дерева Хаффмана и еще некоторых алгоритмов Теории информации

Литература

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: «Вильямс», 2006. — 1296 с. — ISBN 0-07-013151-1
• Д. Сэломон. Сжатие данных, изображения и звука. — М.: Техносфера, 2004. — 368 с. — 3000 экз. — ISBN 5-94836-027-X
• Ананий В. Левитин. Глава 9. Жадные методы: Алгоритм Хаффмана // Алгоритмы: введение в разработку и анализ = Introduction to The Design and Analysis of Aigorithms. — М.: «Вильямс», 2006. — С. 392—398. — ISBN 0-201-74395-7