- Фильтр Чебышева
-
Линейные электронные фильтры Фильтр Баттерворта Фильтр Чебышева Эллиптический фильтр Фильтр Бесселя Фильтр Гаусса Фильтр Лежандра Фильтр Габора Править Фильтр Чебышева — один из типов линейных аналоговых или цифровых фильтров, отличительной особенностью которого является более крутой спад амплитудно-частотной характеристики (АЧХ) и существенные пульсации амплитудно-частотной характеристики на частотах полос пропускания (фильтр Чебышева I рода) и подавления (фильтр Чебышева II рода), чем у фильтров других типов. Фильтр получил название в честь известного русского математика XIX века Пафнутия Львовича Чебышева, так как характеристики этого фильтра основываются на многочленах Чебышева.
Фильтры Чебышева обычно используются там, где требуется с помощью фильтра небольшого порядка обеспечить требуемые характеристики АЧХ, в частности, хорошее подавление частот из полосы подавления, и при этом гладкость АЧХ на частотах полос пропускания и подавления не столь важна.
Различают фильтры Чебышева I и II родов.
Содержание
Фильтр Чебышева I рода
Это более часто встречающаяся модификация фильтров Чебышева. Амплитудно-частотная характеристика такого фильтра
 -го порядка задаётся следующим выражением:
-го порядка задаётся следующим выражением:где
 — показатель пульсаций,
— показатель пульсаций,  — частота среза, а
— частота среза, а  — многочлен Чебышева
— многочлен Чебышева  -го порядка.
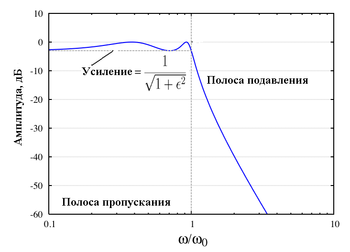
-го порядка.В полосе пропускания такого фильтра видны пульсации, амплитуда которых определяется показателем пульсации (англ. ripple factor)
 . В полосе пропускания многочлены Чебышева принимают значения от 0 до 1, поэтому коэффициент усиления фильтра принимает значения от максимального
. В полосе пропускания многочлены Чебышева принимают значения от 0 до 1, поэтому коэффициент усиления фильтра принимает значения от максимального  до минимального
до минимального  . На частоте среза
. На частоте среза  коэффициент усиления имеет значение
коэффициент усиления имеет значение  , а на частотах выше неё продолжает уменьшаться с увеличением частоты. (Примечание: обычное определение частоты среза как частоты, когда ЛАЧХ имеет значение −3 дБ в случае фильтра Чебышева не работает).
, а на частотах выше неё продолжает уменьшаться с увеличением частоты. (Примечание: обычное определение частоты среза как частоты, когда ЛАЧХ имеет значение −3 дБ в случае фильтра Чебышева не работает).В случае аналогового электронного фильтра Чебышева его порядок равен числу реактивных компонентов (например, индуктивностей), использованных при его реализации.
Пульсации в полосе пропускания часто задаются в децибелах:
Пульсации в дБ =
 .
.Например, пульсации амплитудой в 3 дБ соответствуют
 .
.Более крутой спад характеристики может быть получен если допустить пульсации не только в полосе пропускания, но и в полосе подавления, добавив в передаточную функцию фильтра нулей на мнимой оси
 в комплексной плоскости. Это однако приведёт к меньшему эффективному подавлению в полосе подавления. Полученный фильтр является эллиптическим фильтром, также известным как фильтр Кауэра.
в комплексной плоскости. Это однако приведёт к меньшему эффективному подавлению в полосе подавления. Полученный фильтр является эллиптическим фильтром, также известным как фильтр Кауэра.Полюса и нули
 Логарифм модуля амплитудной характеристики фильтра Чебышева I рода 8-го порядка на плоскости комплексной частоты (
Логарифм модуля амплитудной характеристики фильтра Чебышева I рода 8-го порядка на плоскости комплексной частоты (
 ) при
) при  и
и  . Белые пятна — это полюса фильтра. Они расположены на эллипсе с полуосью 0,3836… по действительной оси и 1,071… по мнимой оси. Полюса передаточной функции фильтра расположены в левой полуплоскости. Чёрный цвет соответствует коэффициенту передачи менее 0,05, белый соответствует коэффициенту передачи более 20.
. Белые пятна — это полюса фильтра. Они расположены на эллипсе с полуосью 0,3836… по действительной оси и 1,071… по мнимой оси. Полюса передаточной функции фильтра расположены в левой полуплоскости. Чёрный цвет соответствует коэффициенту передачи менее 0,05, белый соответствует коэффициенту передачи более 20.Для простоты примем частоту среза равной единице. Полюса
 фильтра Чебышева являются нулями его знаменателя. Используя комплексную частоту
фильтра Чебышева являются нулями его знаменателя. Используя комплексную частоту  , получим:
, получим: .
.
Представив
 и используя тригонометрическое определение многочленов Чебышева, получим:
и используя тригонометрическое определение многочленов Чебышева, получим: .
.
Разрешим последнее выражение относительно

 .
.
Тогда полюса фильтра Чебышева определяются из следующего выражения:

 .
.
Используя свойства тригонометрических и гиперболических функций, запишем последнее выражение в комплексной форме:

 ,
,
где
 и
и .
.
Это выражение можно рассматривать как параметрическое уравнение с параметром
 . Оно показывает, что полюса лежат на эллипсе в
. Оно показывает, что полюса лежат на эллипсе в  -плоскости, причём центр эллипса находится в точке
-плоскости, причём центр эллипса находится в точке  , полуось действительной оси имеет длину
, полуось действительной оси имеет длину  , а полуось мнимой оси имеет длину
, а полуось мнимой оси имеет длину  .
.Передаточная функция
Уравнение, выведенное выше, содержит полюса, относящиеся к комплексному коэффициенту усиления фильтра
 . Для каждого полюса есть комплексно-сопряжённый, а для каждой комплексно-сопряжённой пары есть два полюса, отличающихся от них только знаком действительной части полюса. Передаточная функция должна быть устойчивой, что означает, что её полюса должны иметь отрицательную действительную часть, то есть лежать в левой полуплоскости комплексной плоскости. Передаточная функция в этом случае задаётся следующим выражением:
. Для каждого полюса есть комплексно-сопряжённый, а для каждой комплексно-сопряжённой пары есть два полюса, отличающихся от них только знаком действительной части полюса. Передаточная функция должна быть устойчивой, что означает, что её полюса должны иметь отрицательную действительную часть, то есть лежать в левой полуплоскости комплексной плоскости. Передаточная функция в этом случае задаётся следующим выражением:где
 — только те полюса, которые имеют отрицательную действительную часть.
— только те полюса, которые имеют отрицательную действительную часть.Групповая задержка
Групповая задержка определяется как минус производная фазы фильтра по частоте и является мерой искажения фазы сигнала на различных частотах.
Фазовые характеристики
Фазовые характеристики фильтра Чебышева I рода — фазо-частотная характеристика (ФЧХ) и фазовая задержка — представлены на рисунке. Фазо-частотная характеристика показывает распределение по частоте смещения фазы выходного сигнала относительно входного. Фазовая задержка определяется как частное от деления фазо-частотной характеристики на частоту и характеризует распределение по частоте временного смещения выходного сигнала относительно входного.
Временны́е характеристики
Временные характеристики фильтра Чебышева I рода — импульсная переходная функция и переходная функция — представлены на рисунке. Импульсная переходная функция представляет собой реакцию фильтра на входной сигнал в виде дельта-функции Дирака, а переходная функция — реакцию на входное воздействие в виде единичной функции Хевисайда.
Фильтр Чебышева II рода
Фильтр Чебышева II рода (инверсный фильтр Чебышева) используется реже, чем фильтр Чебышева I рода ввиду менее крутого спада амплитудной характеристики, что приводит к увеличению числа компонентов. У него отсутствуют пульсации в полосе пропускания, однако присутствуют в полосе подавления. Амплитудная характеристика такого фильтра задаётся следующим выражением:
В полосе подавления полиномы Чебышева принимают значения от 0 до 1, из-за чего амплитудная характеристика такого фильтра принимает значения от нуля до
минимальной частотой, при которой достигается этот максимум является частота среза
 . Параметр
. Параметр  связан с затуханием в полосе подавления
связан с затуханием в полосе подавления  в децибелах следующим выражением:
в децибелах следующим выражением:Для затухания на частотах полосы подавления в 5 дБ:
 ; для затухания в 10 дБ:
; для затухания в 10 дБ:  . Частота
. Частота  является частотой среза. Частота затухания в 3 дБ
является частотой среза. Частота затухания в 3 дБ  связана с
связана с  следующим выражением:
следующим выражением: .
.
Полюса и нули
 Логарифм модуля амплитудной характеристики фильтра Чебышева II рода восьмого порядка на комплексной плоскости (
Логарифм модуля амплитудной характеристики фильтра Чебышева II рода восьмого порядка на комплексной плоскости (
 ) с
) с  и
и  . Белые пятна соответствуют полюсам, а чёрные — нулям. Показаны все 16 полюсов. 6 нулей (все нули второго порядка) показаны также, 2 находятся за пределами картинки (один на положительной мнимой оси, другой — на отрицательной мнимой оси). Полюса передаточной функции фильтра — это полюса, находящиеся в левой полуплоскости, нули передаточной функции — это нули модуля амплитудной характеристики фильтра Чебышева, только не второго, а первого порядка. Чёрный цвет соответствует коэффициенту усиления менее 0,01, белый — коэффициенту усиления более 3.
. Белые пятна соответствуют полюсам, а чёрные — нулям. Показаны все 16 полюсов. 6 нулей (все нули второго порядка) показаны также, 2 находятся за пределами картинки (один на положительной мнимой оси, другой — на отрицательной мнимой оси). Полюса передаточной функции фильтра — это полюса, находящиеся в левой полуплоскости, нули передаточной функции — это нули модуля амплитудной характеристики фильтра Чебышева, только не второго, а первого порядка. Чёрный цвет соответствует коэффициенту усиления менее 0,01, белый — коэффициенту усиления более 3.Приняв частоту среза равной единице, получим выражение для полюсов
 фильтра Чебышева:
фильтра Чебышева: .
.
Полюса фильтра Чебышева II рода представляют собой «инверсию» полюсов фильтра Чебышева I рода:

 ,
,
где
 .
.Нули
 фильтра Чебышева II рода определяются из следующего соотношения::
фильтра Чебышева II рода определяются из следующего соотношения:: .
.
Нули фильтра Чебышева II рода являются «инверсией» нулей многочленов Чебышева:
 ,
,
где
 .
.Передаточная функция
Передаточная функция задаётся при помощи полюсов в левой полуплоскости комплексной плоскости, её нули совпадают с нулями модуля амплитудной характеристики, с тем лишь отличием, что их порядок равен 1.
Групповая задержка
Амплитудная характеристика и групповая задержка показаны на графике. Можно видеть, что пульсации амплитуды приходятся на полосу подавления, а не на полосу пропускания.
Фазовые характеристики
Фазовые характеристики фильтра Чебышева II рода — фазо-частотная характеристика и фазовая задержка — представлены на рисунке. Фазо-частотная характеристика показывает распределение по частоте смещения фазы выходного сигнала относительно входного. Фазовая задержка определяется как частное от деления фазо-частотной характеристики на частоту и характеризует распределение по частоте временного смещения выходного сигнала относительно входного.
Временные характеристики
Временные характеристики фильтра Чебышева II рода — импульсная переходная функция и переходная функция — представлены на рисунке. Импульсная переходная функция представляет собой реакцию фильтра на входной сигнал в виде дельта-функции Дирака, а переходная функция — реакцию на входное воздействие в виде единичной функции Хевисайда.
Цифровые фильтры Чебышева
Фильтры Чебышева часто реализуются в цифровой форме. Для того, чтобы от аналогового фильтра перейти к цифровому, необходимо над каждым каскадом фильтра осуществить билинейное преобразование. Весь фильтр получается путём последовательного соединения каскадов. Простой пример фильтра Чебышева низких частот I рода чётного порядка:
Z-преобразование каждого каскада:
 .
.
Во временной области преобразование записывается как:
Коэффициенты
 и
и  подсчитываются из коэффициентов
подсчитываются из коэффициентов  и
и  :
:Для получения фильтра Чебышева более высокого порядка, необходимо соединить последовательно несколько каскадов.
Сравнение с другими линейными фильтрами
Ниже представлены графики АЧХ фильтра Чебышева I и II родов в сравнении с некоторыми другими фильтрами с тем же числом коэффициентов:
По графикам видно, что амплитудная характеристики фильтров Чебышева имеет более крутой спад, чем у фильтров Баттерворта, но не такой крутой, как у эллиптического фильтра.
См. также
- Цифровая обработка сигналов
- Цифровая обработка изображений
- Электронный фильтр
- Решётчатый фильтр
- БИХ-фильтр
Библиография
- В.А. Лукас Теория автоматического управления. — M.: Недра, 1990.
- Б.Х. Кривицкий Справочник по теоретическим основам радиоэлектроники. — М.: Энергия, 1977.
- Richard W. Daniels Approximation Methods for Electronic Filter Design. — New York: McGraw-Hill, 1974. — ISBN 0-07-015308-6
- Steven W. Smith The Scientist and Engineer’s Guide to Digital Signal Processing. — Second Edition. — San-Diego: California Technical Publishing, 1999. — ISBN 0-9660176-4-1
- Britton C. Rorabaugh Approximation Methods for Electronic Filter Design. — New York: McGraw-Hill, 1999. — ISBN 0-07-054004-7
- B. Widrow, S.D. Stearns Adaptive Signal Processing. — Paramus, NJ: Prentice-Hall, 1985. — ISBN 0-13-004029-0
- S. Haykin Adaptive Filter Theory. — 4rd Edition. — Paramus, NJ: Prentice-Hall, 2001. — ISBN 0-13-090126-1
- Michael L. Honig, David G. Messerschmitt Adaptive Filters — Structures, Algorithms, and Applications. — Hingham, MA: Kluwer Academic Publishers, 1984. — ISBN 0-89838-163-0
- J.D. Markel, A.H. Gray, Jr. Linear Prediction of Speech. — New York: Springer-Verlag, 1982. — ISBN 0-387-07563-1
- L. R. Rabiner, R.W. Schafer Digital Processing of Speech Signals. — Paramus, NJ: Prentice-Hall, 1978. — ISBN 0-13-213603-1
- Richard J. Higgins Digital Signal Processing in VLSI. — Paramus, NJ: Prentice-Hall, 1990. — ISBN 0-13-212887-X
- A. V. Oppenheim, R. W. Schafer Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1975. — ISBN 0-13-214635-5
- L. R. Rabiner, B. Gold Theory and Application of Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1986. — ISBN 0-13-914101-4
- John G. Proakis, Dimitris G. Manolakis Introduction to Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1988. — ISBN 0-02-396815-X
Ссылки

Фильтр Чебышева на Викискладе? - Расчёт фильтра Чебышева первого рода с примерами
- Расчёт фильтра Чебышева второго рода с примерами
- Лекция по цифровой фильтрации
- Фильтры нижних частот
- Расчёт рекурсивных фильтров
- Классификация фильтров
- Сравнение линейных фильтров (англ.)
В данной статье или разделе имеется список источников или внешних ссылок, но источники отдельных утверждений остаются неясными из-за отсутствия сносок. Вы можете улучшить статью, внеся более точные указания на источники.Категория:- Фильтрация
Wikimedia Foundation. 2010.





 . Видно, что в полосе пропускания и АЧХ и групповая задержка имеют пульсации, в полосе подавления этих пульсаций нет.
. Видно, что в полосе пропускания и АЧХ и групповая задержка имеют пульсации, в полосе подавления этих пульсаций нет.











![y[n]=\alpha_0 \cdot x[0] + \alpha_1 \cdot x[-1] + \alpha_2 \cdot x[-2] - \beta_1 \cdot y[-1] - \beta_2 \cdot y[-2]](74185b1e8b0681dea789dce9cb863866.png)












