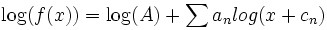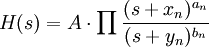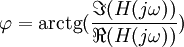- ЛАЧХ
-
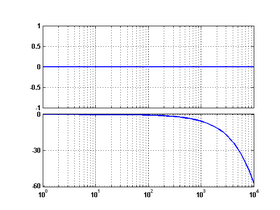
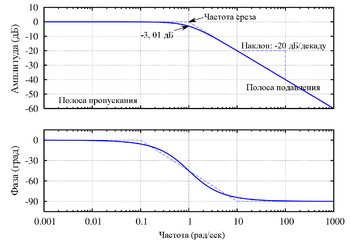 ЛАФЧХ фильтра Баттерворта первого порядка
ЛАФЧХ фильтра Баттерворта первого порядкаЛогарифмическая амплитудно-фазовая частотная характеристика (ЛАФЧХ) — представление частотного отклика линейной стационарной системы в логарифмическом масштабе.
ЛАФЧХ строится в виде двух графиков: логарифмической амплитудно-частотной характеристики и фазо-частотной характеристики, которые обычно располагаются друг под другом.
Анализ систем с помощью ЛАФЧХ весьма прост и удобен, поэтому находит широкое применение в различных отраслях техники, таких как цифровая обработка сигналов, электротехника и теория управления.
Содержание
Названия
В западной литературе используется название диаграмма Боде или график Боде, по имени выдающегося инженера Хенрика Боде (англ. Hendrik Wade Bode).
В инженерных кругах название обычно сокращается до ЛАХ.
В пакете прикладных программ для инженерных вычислений bode.
Использование
Свойства и особенности
Если передаточная функция системы является рациональной, тогда ЛАФЧХ может быть аппроксимирована прямыми линиями. Это удобно при рисовании ЛАФЧХ вручную, а также при составлении ЛАФЧХ простых систем.
С помощью ЛАФЧХ удобно проводить синтез систем систем управления, а также цифровых и аналоговых фильтров: в соответствии с определёнными критериями качества строится желаемая ЛАФЧХ, аппроксимированная с помощью прямых линий, которая затем разбивается на ЛАФЧХ отдельных элементарных звеньев, из которых восстанавливается передаточная функция системы (регулятора) или фильтра.
ЛАЧХ
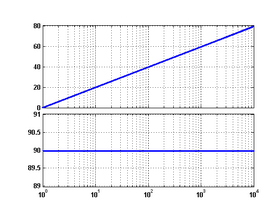
На графике ЛАЧХ абсциссой является частота в логарифмическом масштабе, по оси ординат отложена амплитуда передаточной функции в децибелах.
Представление АЧХ в логарифмическом масштабе упрощает построение характеристик сложных систем, так как позволяет заменить операцию перемножения АЧХ звеньев сложением, что вытекает из свойства логарифма:
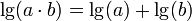 .
.ФЧХ
На графике фазо-частотной характеристики абсциссой является частота в логарифмическом масштабе, по оси ординат отложен фазовый сдвиг выходного сигнала системы относительно входного (обычно в градусах).
Также возможен вариант, когда по оси ординат откладывается фазовый сдвиг в логарифмическом масштабе, в этом случае характеристика будет называться ЛФЧХ.
Случай минимально-фазовых систем
Амлитуда и фаза системы редко меняются независимо друг от друга — при изменении амплитуды меняется и фаза и наоборот. Для минимально-фазовых систем ЛФЧХ и ЛАЧХ могут быть однозначно определены друг из друга с помощью преобразования Гильберта.
Построение ЛАФЧХ
Основная идея основывается на следующем математическом правиле сложения логарифмов. Если передаточную функцию можно представить в виде дробно-рациональной функции
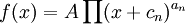 ,
,
то:
После разбиения передаточной функции на элементарные звенья можно построить ЛАФЧХ каждого отдельного звена, а результирующую ЛАФЧХ получить простым сложением.
Аппроксимация ЛАЧХ прямыми линиями
При построении ЛАЧХ для оси ординат обычно используется масштаб
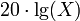 , то есть значение АЧХ, равное 100 превращается в 40 децибел шкалы ЛАЧХ. Если передаточная функция имеет вид:
, то есть значение АЧХ, равное 100 превращается в 40 децибел шкалы ЛАЧХ. Если передаточная функция имеет вид:- где
 — комплексная переменная, которую можно связать с частотой, используя следующую формальную замену:
— комплексная переменная, которую можно связать с частотой, используя следующую формальную замену: 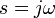 ,
, 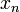 и
и 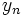 — константы, а
— константы, а 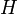 — передаточная функция. Тогда построить ЛАЧХ можно используя следующие правила:
— передаточная функция. Тогда построить ЛАЧХ можно используя следующие правила:
-
-
- в каждом
 , где
, где  (нуль), наклон линии увеличивается на
(нуль), наклон линии увеличивается на 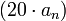 дБ на декаду.
дБ на декаду.
- в каждом
-
-
-
- в каждом
 , где
, где 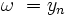 (полюс), наклон линии уменьшается на
(полюс), наклон линии уменьшается на 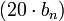 дБ на декаду.
дБ на декаду.
- в каждом
-
-
-
- Начальное значение графика можно найти простой подстановкой значения круговой частоты
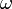 в передаточную функцию.
в передаточную функцию.
- Начальное значение графика можно найти простой подстановкой значения круговой частоты
-
-
-
- Начальный наклон графика зависит от числа и порядка нулей и полюсов, которые меньше начального значения частоты. Он может быть найден с помощью первых двух правил.
-
-
-
- В случае наличия комплексно-сопряжённых нулей или полюсов необходимо использовать звенья второго порядка,
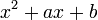 , наклон менятся в точке
, наклон менятся в точке 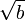 сразу на
сразу на 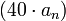 дБ на декаду.
дБ на декаду.
- В случае наличия комплексно-сопряжённых нулей или полюсов необходимо использовать звенья второго порядка,
-
Корректировка аппроксимированной ЛАЧХ
Для корректировки ЛАЧХ, аппроксимированную прямыми линиями надо:
-
-
- в каждом нуле поставить точку на
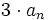 дБ выше линии (
дБ выше линии (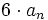 дБ для двух комплексно-сопряжённых нулей)
дБ для двух комплексно-сопряжённых нулей)
- в каждом нуле поставить точку на
-
-
-
- в каждом полюсе поставить точку на
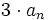 дБ ниже линии (
дБ ниже линии (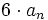 дБ для двух комплексно-сопряжённых полюсов)
дБ для двух комплексно-сопряжённых полюсов)
- в каждом полюсе поставить точку на
-
-
-
- плавно соединить точки, используя прямые линии в качестве асимптот
-
Аппроксимация ФЧХ
Для построения аппроксимированной ФЧХ используют запись передаточной функции в том же виде, что и для ЛАЧХ:
Основной принцип построения ФЧХ — начертить отдельные графики для каждого полюса или нуля, затем сложив их. Точная кривая фазо-частотной характеристики задаётся уравнением:
Для того, чтобы нарисовать ФЧХ для каждого полюса или нуля, используют следующие правила:
-
- если
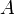 положительно, начать линию (с нулевым наклоном) в 0 градусов,
положительно, начать линию (с нулевым наклоном) в 0 градусов, - если
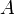 отрицательно, начать линию (с нулевым наклоном) в 180 градусов,
отрицательно, начать линию (с нулевым наклоном) в 180 градусов, - для нуля сделать наклон линии вверх на
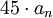 (
(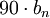 для комплексно сопряжённого) градусов на декаду начиная с
для комплексно сопряжённого) градусов на декаду начиная с 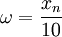 ,
, - для полюса наклонить линию вниз на
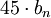 (
(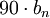 для комплексно сопряжённого) градусов на декаду начиная с
для комплексно сопряжённого) градусов на декаду начиная с 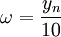 ,
, - обнулить наклон снова когда фаза изменится на
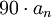 градусов для простого нуля или полюса и на
градусов для простого нуля или полюса и на 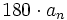 градусов для комплексно-сопряжённого нуля или полюса,
градусов для комплексно-сопряжённого нуля или полюса, - сложить все линии и нарисовать результирующую.
- если
Анализ устойчивости по ЛАФЧХ
ЛАФЧХ некоторых элементарных звеньев
Ниже представлена таблица, в которую помещены передаточные функции и ЛАФЧХ некоторых типовых элементарных звеньев. Большая часть линейных стационарных систем может быть представлена в виде соединения таких звеньев. В таблице
 — комплексная переменная.
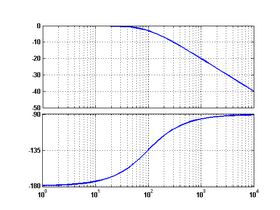
— комплексная переменная.№ Звено Передаточная функция ЛАФЧХ Примечания 1 пропорциональное 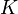
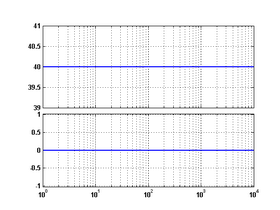
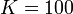
2 идеальное интегрирующее[1] 
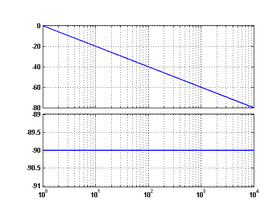
3 идеальное дифференцирующее[2] 
4 апериодическое
(реальное интегрирующее)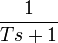
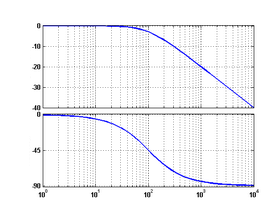

5 колебательное 
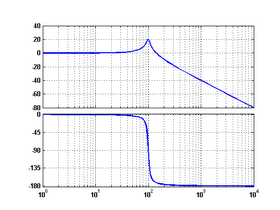

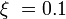
6 неустойчивое
апериодическое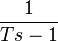

неминимально-фазовое7 форсирующее 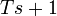
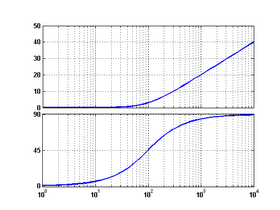

8 форсирующее
второго
порядка
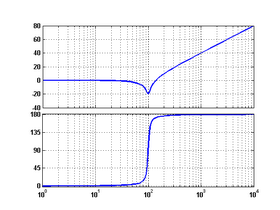

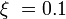
9 чистого
запаздывание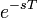
Примечания
См. также
Wikimedia Foundation. 2010.