- Простой кусок поверхности
-
 Пример простой поверхности
Пример простой поверхностиПове́рхность — традиционное название для двумерного многообразия в пространстве.
Поверхности определяется как множество точек, координаты которых удовлетворяют определённому виду уравнений:
Если функция
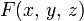 непрерывна в некоторой точке и имеет в ней непрерывные частные производные, по крайней мере одна из которых не обращается в нуль, то в окрестности этой точки поверхность, заданная уравнением (1), будет правильной поверхностью.
непрерывна в некоторой точке и имеет в ней непрерывные частные производные, по крайней мере одна из которых не обращается в нуль, то в окрестности этой точки поверхность, заданная уравнением (1), будет правильной поверхностью.Помимо указанного выше неявного способа задания поверхность может быть определена явно, если одну из переменных, например z, можно выразить через остальные:
Также существует параметрический способ задания. В этом случае поверхность определяется системой уравнений:
Содержание
Понятие о простой поверхности
Подробней в статье Простая поверхность. Основным является понятие простой поверхности, которую можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям).
Более точно, простой поверхностью называется образ гомеоморфного отображения (то есть взаимно однозначного и взаимно непрерывного отображения) внутренности единичного квадрата. Этому определению можно дать аналитическое выражение.
Пусть на плоскости с прямоугольной системой координат u и v задан квадрат, координаты внутренних точек которого удовлетворяют неравенствам 0 < u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u', v') были различными соответствующие точки (x, у, z) и (x', у', z').
Примером простой поверхности является полусфера. Вся же сфера не является простой поверхностью. Это вызывает необходимость дальнейшего обобщения понятия поверхности.
Подмножество пространства, у каждой точки которого есть окрестность, являющаяся простой поверхностью, называется правильной поверхностью.
Поверхность в дифференциальной геометрии
В дифференциальной геометрии исследуемые поверхности обычно подчинены условиям, связанным с возможностью применения методов дифференциального исчисления. Как правило, это — условия гладкости поверхности, то есть существования в каждой точке поверхности определённой касательной плоскости, кривизны и т. д. Эти требования сводятся к тому, что функции, задающие поверхность, предполагаются однократно, дважды, трижды, а в некоторых вопросах — неограниченное число раз дифференцируемыми или даже аналитическими функциями. При этом дополнительно накладывается условие регулярности.
Случай неявного задания. Поверхность, заданная уравнением
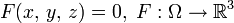 , является гладкой регулярной поверхностью, если
, является гладкой регулярной поверхностью, если 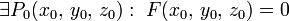 , функция F непрерывно дифференцируема в своей области определения Ω, а её частные производные одновременно не обращаются в нуль (условие правильности) на всём множестве Ω:
, функция F непрерывно дифференцируема в своей области определения Ω, а её частные производные одновременно не обращаются в нуль (условие правильности) на всём множестве Ω:Случай параметрического задания. Зададим поверхность векторным уравнением
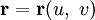 , или, что то же самое, тремя уравнениями в координатах:
, или, что то же самое, тремя уравнениями в координатах:Эта система уравнений задаёт гладкую регулярную поверхность, если выполнены условия:
- система устанавливает взаимно однозначное соответствие между образом и прообразом Ω;
- функции
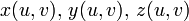 непрерывно дифференцируемы в Ω;
непрерывно дифференцируемы в Ω; - выполнено условие невырожденности:
Геометрически последнее условие означает, что векторы
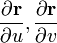 нигде не параллельны.
нигде не параллельны. Координатная сетка на сфере
Координатная сетка на сфереПараметры u, v можно рассматривать как внутренние координаты точек поверхности. Фиксируя одну из координат, мы получаем два семейства координатных кривых, покрывающих поверхность координатной сеткой.
Случай явного задания. Поверхность S может быть определена как график функции z = f(x,y); тогда S является гладкой регулярной поверхностью, если функция f дифференцируема. Этот вариант можно рассматривать как частный случай параметрического задания:
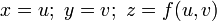 .
.Касательная плоскость
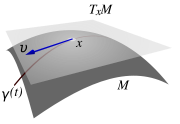 Касательная плоскость в точке поверхности.
Касательная плоскость в точке поверхности.Касательная плоскость в точке гладкой поверхности — это плоскость, имеющая максимальный порядок соприкосновения с поверхностью в этой точке. Эквивалентный вариант определения: касательная плоскость есть плоскость, содержащая касательные ко всем гладким кривым, проходящим через эту точку.
Пусть гладкая кривая на параметрически заданной поверхности
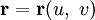 задана в виде:
задана в виде: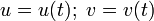 .
.
Направление
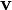 касательной к такой кривой даёт вектор:
касательной к такой кривой даёт вектор:Отсюда видно, что все касательные ко всем кривым в данной точке лежат в одной плоскости, содержащей векторы
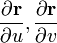 , которые мы выше предположили независимыми.
, которые мы выше предположили независимыми.Уравнение касательной плоскости в точке
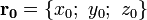 имеет вид:
имеет вид: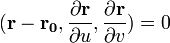 (смешанное произведение векторов).
(смешанное произведение векторов).
В координатах уравнения касательной плоскости для разных способов задания поверхности приведены в таблице:
касательная плоскость к поверхности в точке 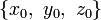
неявное задание 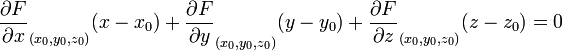
явное задание 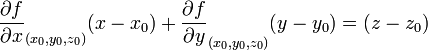
параметрическое задание 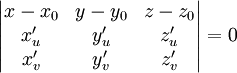
Метрика и внутренняя геометрия
Вновь рассмотрим гладкую кривую:
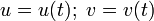 .
.
Элемент её длины определяется из соотношения:
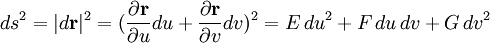 ,
,
где
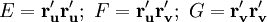 .
.Эта квадратичная форма называется первой квадратичной формой и представляет собой двумерный вариант метрики поверхности. Для регулярной поверхности её дискриминант EG − F2 > 0 во всех точках. Коэффициент
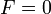 в точке поверхности тогда и только тогда, когда в этой точке координатные кривые ортогональны. В частности, на плоскости с декартовыми координатами
в точке поверхности тогда и только тогда, когда в этой точке координатные кривые ортогональны. В частности, на плоскости с декартовыми координатами 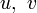 получается метрика ds2 = du2 + dv2 (теорема Пифагора).
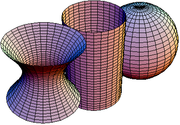
получается метрика ds2 = du2 + dv2 (теорема Пифагора).Метрика не определяет однозначно форму поверхности. Например, метрика геликоида и катеноида, параметризованных соответствующим образом, совпадает, то есть между их областями существует соответствие, сохраняющее все длины (изометрия). Свойства, сохраняющиеся при изометрических преобразованиях, называются внутренней геометрией поверхности. Внутренняя геометрия не зависит от положения поверхности в пространстве и не меняется при её изгибании без растяжения и сжатия (например, при изгибании цилиндра в конус).
Метрические коэффициенты
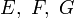 определяют не только длины всех кривых, но и вообще результаты всех измерений внутри поверхности (углы, площади, кривизна и др.). Поэтому всё, что зависит только от метрики, относится к внутренней геометрии.
определяют не только длины всех кривых, но и вообще результаты всех измерений внутри поверхности (углы, площади, кривизна и др.). Поэтому всё, что зависит только от метрики, относится к внутренней геометрии.Нормаль и нормальное сечение
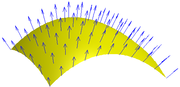 Векторы нормали в точках поверхности
Векторы нормали в точках поверхностиОдной из основных характеристик поверхности является её нормаль — единичный вектор, перпендикулярный касательной плоскости в заданной точке:
![\mathbf{m} = \frac{[\mathbf{r'_u}, \mathbf{r'_v}]} {|[\mathbf{r'_u}, \mathbf{r'_v}]|}](/pictures/wiki/files/97/a9c39cc4556ffb973cc3072cfdc67425.png) .
.
Знак нормали зависит от выбора координат.
Сечение поверхности плоскостью, содержащей нормаль (в данной точке), образует некоторую кривую на поверхности, которая называется нормальным сечением поверхности. Главная нормаль для нормального сечения совпадает с нормалью к поверхности (с точностью до знака).
Если же кривая на поверхности не является нормальным сечением, то её главная нормаль образует с нормалью поверхности некоторый угол θ. Тогда кривизна k кривой связана с кривизной kn нормального сечения (с той же касательной) формулой Мёнье:
Координаты орта нормали для разных способов задания поверхности приведены в таблице:
Координаты нормали в точке поверхности неявное задание 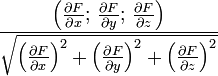
явное задание 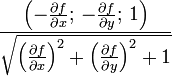
параметрическое задание 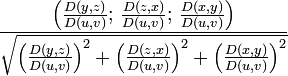
Здесь
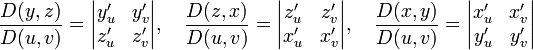 .
.Кривизна
Для разных направлений в заданной точке поверхности получается разная кривизна нормального сечения, которая называется нормальной кривизной; ей приписывается знак плюс, если главная нормаль кривой идёт в том же направлении, что и нормаль к поверхности, или минус, если направления нормалей противоположны.
Вообще говоря, в каждой точке поверхности существуют два перпендикулярных направления e1 и e2, в которых нормальная кривизна принимает минимальное и максимальное значения; эти направления называются главными. Исключение составляет случай, когда нормальная кривизна по всем направлениям одинакова (например, у сферы или на торце эллипсоида вращения), тогда все направления в точке — главные.
Поверхности с отрицательной (слева), нулевой (в центре) и положительной (справа) кривизной.Нормальные кривизны в главных направлениях называются главными кривизнами; обозначим их κ1 и κ2. Величина:
- K = κ1κ2
называется гауссовой кривизной, полной кривизной или просто кривизной поверхности. Встречается также термин скаляр кривизны, который подразумевает результат свёртки тензора кривизны; при этом скаляр кривизны вдвое больше, чем гауссова кривизна.
Гауссова кривизна может быть вычислена через метрику, и поэтому она является объектом внутренней геометрии поверхностей (отметим, что главные кривизны к внутренней геометрии не относятся). По знаку кривизны можно классифицировать точки поверхности (см. рисунок). Кривизна плоскости равна нулю. Кривизна сферы радиуса R всюду равна
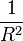 . Существует и поверхность постоянной отрицательной кривизны — псевдосфера.
. Существует и поверхность постоянной отрицательной кривизны — псевдосфера.Геодезические линии, геодезическая кривизна
Кривая на поверхности называется геодезической линией, или просто геодезической, если во всех её точках главная нормаль к кривой совпадает с нормалью к поверхности. Пример: на плоскости геодезическими будут прямые и отрезки прямых, на сфере - большие круги и их отрезки.
Эквивалентное определение: у геодезической линии проекция её главной нормали на соприкасающуюся плоскость есть нулевой вектор. Если кривая не является геодезической, то указанная проекция ненулевая; её длина называется геодезической кривизной kg кривой на поверхности. Имеет место соотношение:
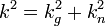 ,
,
где k - кривизна данной кривой, kn - кривизна её нормального сечения с той же касательной.
Геодезические линии относятся к внутренней геометрии. Перечислим их главные свойства.
- Через данную точку поверхности в заданном направлении проходит одна и только одна геодезическая.
- На достаточно малом участке поверхности две точки всегда можно соединить геодезической, и притом только одной. Пояснение: на сфере противоположные полюса соединяет бесконечное количество меридианов, а две близкие точки можно соединить не только отрезком большого круга, но и его дополнением до полной окружности, так что однозначность соблюдается только в малом.
- Геодезическая является кратчайшей. Более строго: на малом куске поверхности кратчайший путь между заданными точками лежит по геодезической.
Площадь
Ещё один важный атрибут поверхности — её площадь, которая вычисляется по формуле:
Здесь
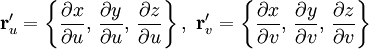 .
.В координатах получаем:
явное задание параметрическое задание выражение для площади 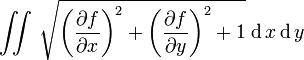
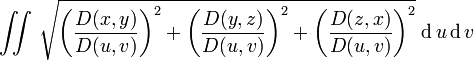
Ориентация
 Лента Мёбиуса.
Лента Мёбиуса.Также важной характеристикой поверхности является её ориентация.
Поверхность называется двусторонней, если на всей её протяжённости она обладает непрерывным вектором нормали. В противном случае поверхность называют односторонней.
Ориентированной называется двусторонняя поверхность с выбранным направлением нормали.
Примерами односторонних, а следовательно и неориентируемых поверхностей являются бутылка Клейна или лента Мёбиуса.
Типы поверхностей
С точки зрения топологического строения, поверхности как двумерные многообразия бывают:
- замкнутые и открытые,
- ориентируемые и неориентируемые
- и т. д.
Обобщение
О многомерных аналогах теории см.:
Литература
- Ильин В.А., Позняк Э.Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
- Кудрявцев Л.Д. Курс математического анализа. — М.: Дрофа. — 570 с.
- Погорелов А. И. Дифференциальная геометрия. — 6-е издание. — М.: Наука, 1974.
- Рашевский П. К. Курс дифференциальной геометрии. — 3-е издание. — М.: ГИТТЛ, 1950.
-
Wikimedia Foundation. 2010.

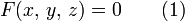
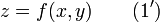
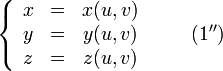
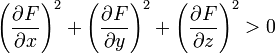
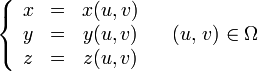
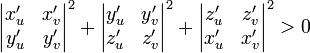
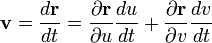
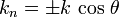
![S=\iint\,|[\mathbf{r}'_u\times\mathbf{r}'_v]|\;\mathrm{d}\,u\,\mathrm{d}\,v](/pictures/wiki/files/55/799ccd87f8fb7e9812748e2fdef805a6.png)