Бутылка Клейна

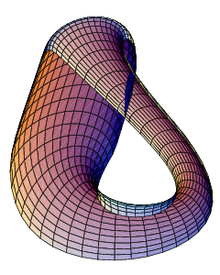
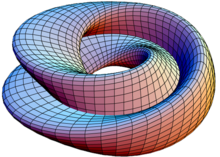
Бутылка Клейна, погружённая в трёхмерное пространство.

Бутылка Клейна — это определённая неориентируемая поверхность (то есть двумерное многообразие). Бутылка Клейна впервые была описана в 1882 г. немецким математиком Ф. Клейном. Она тесно связана с лентой Мёбиуса и проективной плоскостью. Название, по-видимому, происходит от неправильного перевода немецкого слова Fläche (поверхность), которое в немецком языке близко по написанию к слову Flasche (бутылка); затем это название вернулось в таком виде в немецкий.

Чтобы построить модель бутылки Клейна, необходимо взять бутылку с двумя отверстиями: в донышке и в стенке, вытянуть горлышко, изогнуть его вниз, и продев его через отверстие в стенке бутылки (для настоящей бутылки Клейна в четырёхмерном пространстве это отверстие не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве), присоединить к отверстию на дне бутылки.

В отличие от обыкновенного стакана у этого объекта нет «края», где бы поверхность резко заканчивалась. В отличие от воздушного шара можно пройти путь изнутри наружу не пересекая поверхность (то есть на самом деле у этого объекта нет «внутри» и нет «снаружи»).

Более формально, бутылку Клейна можно получить склеиванием квадрата $[0,1]\times [0,1]$, идентифицируя точки (0,y) ~ (1,y) при $0\leqslant y\leqslant 1$ и (x,0) ~ (1-x,1) при $0\leqslant x \leqslant 1$, как показано на диаграмме.

Свойства

• Подобно ленте Мёбиуса, бутылка Клейна является двумерным дифференцируемым неориентируемым многообразием. В отличие от ленты Мёбиуса, бутылка Клейна является замкнутым многообразием, то есть компактным многообразием без края.
• Бутылка Клейна не может быть вложена (только погружена) в трёхмерное евклидово пространство $\R^3$, но вкладывается в $\R^4$.
• Бутылка Клейна может быть получена склеиванием двух лент Мёбиуса по краю. Однако в обычном трехмерном евклидовом пространстве $\R^3$ сделать это, не создав самопересечения, невозможно.
• Хроматическое число поверхности равно 6.

Рассечения

При рассечении бутылки Клейна получается лента Мёбиуса

Реализация бутылки Клейна в виде восьмерки

Если разрезать бутылку Клейна пополам вдоль её оси симметрии, то результатом будет лента Мёбиуса, изображенная справа (необходимо помнить, что изображенного пересечения на самом деле нет).

Параметризация

Бутылка Клейна в виде восьмёрки имеет довольно простую параметризацию:

$x = \left(r + \cos\frac{u}{2}\sin v - \sin\frac{u}{2}\sin 2v\right) \cos u$

$y = \left(r + \cos\frac{u}{2}\sin v - \sin\frac{u}{2}\sin 2v\right) \sin u$

$z = \sin\frac{u}{2}\sin v + \cos\frac{u}{2}\sin 2v$

В этом виде самопересечение имеет форму геометрического круга в плоскости XY. Константа $r$ равна радиусу круга. Параметр $u$ задаёт угол на плоскости XY и $v$ обозначает положение около 8-образного сечения.

Бутылка Клейна в культуре

Стеклянная бутылка Клейна

• Изредка встречается сувенир в виде стеклянной бутылки Клейна. Для изготовления такой бутылки нужен стеклодув высокой квалификации. В том месте, где бутылка пересекает сама себя, приходится оставлять отверстие, чтобы внутреннее пространство бутылки не было изолированным.
• В сериале «Футурама» в серии «The Route of All Evil» на полке показано пиво Klein’s, которое разлито в бутылки Клейна.
• В рассказе математика и писателя Мартина Гарднера «Остров пяти красок» в бутылке Клейна исчезает один из героев произведения.
• В рассказе писателя Дэна Шорина «Бутылочка профессора Клейна», входящем в межавторский цикл Южная Пристань в качестве сюжетообразующего элемента рассматривается гомеоморфность бутылки Клейна.
• В рассказе Брюса Эллиота «Последний иллюзионист» бутылка Клейна используется для мести ассистентом фокусника за смертельно опасную беременность марсианской девушки. Из-за преднамеренной ошибки ассистента фокусник застревает в горлышке огромной бутылки Клейна, наполовину внутри бутылки, наполовину вне её. Автором рассказа утверждается, что фокусника нельзя освободить, т.к. бутылку Клейна нельзя разбить, не разрезав застрявшего фокусника пополам.
• В книге Александра Митича «Игра в поддавки» герои попадают в пространство, подобное бутылке Клейна
• Бутылке Клейна посвящён один их шуточных лимериков Джеймса Линдона^[1]:

     Некто Клейн, не любивший вина,
     Раз придумал бутылку без дна.
       Восклицал он: «К тому же
       Что внутри — в ней снаружи!
     Даже пробка совсем не нужна!»

См. также

• Топология
• Алгебраическая топология
• Поверхность
• Лента Мёбиуса

Примечания

1. ↑ Матвеев, Михаил. Путешествие по ПаЛиндондромии с Джеймсом Линдоном // Знание-сила. - 2012. - № 3. - С. 110-116 . - ISSN 0130-1640. В оригинале:

     An anti-strong-drinker named Klein
     Invented a bottle for wine.
       «There's no stopper», he cried,
       «And it has no inside,
     So the grapes have to stay on the vine!»

   См. также Klein Bottle Cartoons, Limericks, Rhymes, and Haiku

Ссылки

	Бутылка Клейна на Викискладе?

• Топология для школьников
• Магазин стеклянных бутылок Клейна
• Игры Торус Свободно распространяемые игры для Windows и Mac OS X, иллюстрирующие топологию тора и бутылки Клейна
• Анимационный фильм о Бутылке Клейна, созданный в 2010 г. при Свободном Университете г. Берлин (Freie Universität Berlin), включает изображение поездки по Бутылке и изначальное описание Феликса Клейна.

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 13 мая 2011.