- Проблемы Гилберта
-
Проблемы Гильберта — список из 23 кардинальных проблем математики, представленный Давидом Гильбертом на II Международном Конгрессе математиков в Париже в 1900 году. Тогда эти проблемы (охватывающие основания математики, алгебру, теорию чисел, геометрию, топологию, алгебраическую геометрию, группы Ли, вещественный и комплексный анализ, дифференциальные уравнения, математическую физику и теорию вероятностей, а также вариационное исчисление) не были решены. На данный момент решены 16 проблем из 23. Ещё 2 не являются корректными математическими проблемами (одна сформулирована слишком расплывчато, чтобы понять, решена она или нет, другая, далёкая от решения, — физическая, а не математическая). Из оставшихся 5 проблем две не решены никак, а три решены только для некоторых случаев.
Содержание
Список проблем
1 нет консенсуса[1] Проблема Кантора о мощности континуума (Континуум-гипотеза) 2 нет консенсуса[2] Непротиворечивость аксиом арифметики. 3 решена Равносоставность равновеликих многогранников 4 слишком расплывчатая[3] Перечислить метрики, в которых прямые являются геодезическими 5 решена Все ли непрерывные группы являются группами Ли? 6 не математическая Математическое изложение аксиом физики 7 решена Доказать, что число 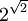 является трансцендентным (или хотя бы иррациональным). [4]
является трансцендентным (или хотя бы иррациональным). [4]8 открыта[5] Проблема простых чисел (гипотеза Римана и проблема Гольдбаха) 9 частично решена[6] Доказательство наиболее общего закона взаимности в любом числовом поле 10 решена[7] Задача о разрешимости диофантовых уравнений 11 решена Исследование квадратичных форм с произвольными алгебраическими числовыми коэффициентами 12 открыта Распространение теоремы Кронекера об абелевых полях на произвольную алгебраическую область рациональности 13 решена Невозможность решения общего уравнения седьмой степени с помощью функций, зависящих только от двух переменных 14 решена Доказательство конечной порождённости алгебры инвариантов алгебраической группы[8] 15 частично решена Строгое обоснование исчислительной геометрии Шуберта 16 частично решена[9] Топология алгебраических кривых и поверхностей[10] 17 решена Представление определённых форм в виде суммы квадратов (см. Семнадцатая проблема Гильберта) 18 решена[11][12] Конечность числа кристаллографических групп; нерегулярные заполнения пространства конгруэнтными многогранниками; наиболее плотная упаковка шаров(решена???) 19 решена Всегда ли решения регулярной вариационной задачи Лагранжа являются аналитическими? 20 решена Общая задача о граничных условиях (?) 21 решена Доказательство существования линейных дифференциальных уравнений с заданной группой монодромии 22 решена Униформизация аналитических зависимостей с помощью автоморфных функций 23 решена Развитие методов вариационного исчисления 24-я проблема
Изначально список содержал 24 проблемы, но в процессе подготовки к докладу Гильберт отказался от одной из них. Эта проблема была связана с теорией доказательств критерия простоты и общих методов. Данная проблема была обнаружена в заметках Гильберта немецким историком науки Рюдигером Тиле в 2000 году[13].
Сноски
- ↑ Результаты Гёделя и Коэна (Cohen) показывают, что ни континуум-гипотеза, ни её отрицание не противоречит системе аксиом Цермело — Френкеля (стандартной системе аксиом теории множеств). Таким образом, континуум-гипотезу в этой системе аксиом невозможно ни доказать, ни опровергнуть (при условии, что эта система аксиом непротиворечива). Ведутся споры о том, является ли результат Коэна полным решением задачи.
- ↑ Курт Гёдель доказал, что непротиворечивость аксиом арифметики нельзя доказать, исходя из самих аксиом арифметики (если только арифметика не является на самом деле противоречивой).
- ↑ Согласно Рову (Rowe) и Грею (Gray) (см. далее), большинство проблем были решены. Некоторые из них не были достаточно точно сформулированы, однако достигнутые результаты позволяют рассматривать их как «решённые». Ров и Грей говорят о четвёртой проблеме как о такой, которая слишком нечётко поставлена, чтобы судить о том, решена она или нет.
- ↑ Решена Зигелем и Гельфондом (и независимо Шнайдером) в более общем виде: если a ≠ 0, 1 — алгебраическое число, и b — алгебраическое, но иррациональное, то ab — трансцендентное число
- ↑ Проблема № 8 содержит две известные проблемы, обе из которых остаются нерешёнными. Первая из них, гипотеза Римана, является одной из семи Проблем тысячелетия, которые были обозначены как «Проблемы Гильберта» 21-го века.
- ↑ Проблема № 9 была решена для абелевого случая; неабелев случай остаётся нерешённым.
- ↑ Юрий Матиясевич в 1970 году доказал алгоритмическую неразрешимость вопроса о том, имеет ли произвольное диофантово уравнение хотя бы одно решение.
- ↑ Утверждение о конечной порождённости алгебры инвариантов доказано для редуктивных групп. Нагата в 1958 году построил пример унипотентной группы, у которой алгебра инвариантов не является конечно порождённой. В. Л. Попов доказал, что если алгебра инвариантов любого действия алгебраической группы G на аффинном алгебраическом многообразии конечно порождена, то группа G редуктивна.
- ↑ Первая (алгебраическая) часть проблемы № 16 более точно формулируется так. Харнаком доказано, что максимальное число овалов равно M=(n-1)(n-2)/2+1, и что такие кривые существуют — их называют M-кривыми. Как могут быть расположены овалы M-кривой? Эта задача сделана до степени n=6 включительно, а для степени n=8 довольно много известно (хотя её ещё не добили). Кроме того, есть общие утверждения, ограничивающие то, как овалы M-кривых могут быть расположены — см. работы Гудкова, Арнольда, Роона, самого Гильберта (впрочем, стоит учитывать, что в доказательстве Гильберта для n=6 есть ошибка: один из случаев, считаемый им невозможным, оказался возможным и был построен Гудковым). Вторая (дифференциальная) часть остаётся открытой даже для квадратичных векторных полей — неизвестно даже, сколько их может быть, и что оценка сверху существует. Даже индивидуальная теорема конечности (то, что у каждого полиномиального векторного поля имеется конечное число предельных циклов) была доказана только недавно. Она считалась доказанной Дюлаком, но в его доказательстве была обнаружена ошибка, и окончательно эта теорема была доказана Ильяшенко и Экалем — для чего каждому из них пришлось написать по книге.
- ↑ Приведен перевод исходного названия проблемы, данного Гильбертом: «16. Problem der Topologie algebraischer Curven und Flächen»(нем.). Однако, более точно её содержание (как оно рассматривается сегодня) можно было бы передать следующим названием: «Число и расположение овалов вещественной алгебраической кривой данной степени на плоскости; число и расположение предельных циклов полиномиального векторного поля данной степени на плоскости». Вероятно (как можно увидеть из английского перевода текста анонса(англ.)), Гильберт считал, что дифференциальная часть (в реальности оказавшаяся значительно труднее алгебраической) будет поддаваться решению теми же методами, что и алгебраическая, и потому не включил её в название.
- ↑ Bieberbach L. Über die Bewegungsgruppen der Euklidischen Raume I.—Math. Ann., 1911, 70, S. 297—336; 1912, 72, S. 400—412.
- ↑ Ров и Грей также называют проблему № 18 «открытой» в своей книге за 2000 год, потому что задача упаковки шаров (известная также как задача Кеплера) не была решена к тому времени, однако на сегодняшний день есть сведения о том, что она уже решена (см. далее). Продвижения в решении проблемы № 16 были сделаны в недавнее время, а также в 1990-х.
- ↑ http://www.maa.org/news/Thiele.pdf
См. также
- Гипотеза Римана
- Континуум гипотеза
- Проблема Гольдбаха
- Диофантовы уравнения
- Проблемы тысячелетия
- Открытые математические проблемы
- Семнадцатая проблема Гильберта
Литература
- Оригинальный текст на немецком доклада Гильберта
- Русский перевод доклада Гильберта (вводная часть и заключение)
- Проблемы Гильберта, Сборник под редакцией П.С. Александрова, М., Наука, 1969 г., 240 с.
- А. А. Болибрух Проблемы Гильберта (100 лет спустя). — МЦНМО, 1999. — Т. 2. — 24 с. — (Библиотека «Математическое просвещение»).
- К конференции 2000 года «Математика и её приложения» библиотека МГТУ им.Н.Э.Баумана подготовила выставку «Проблемы Гильберта», также список трудов Д. Гильберта
- Ляшко С.И., Номировский Д.А., Петунин Ю.И., Семенов В.В. Двадцатая проблема Гильберта. Обобщенные решения операторных уравнений. — М.: «Диалектика», 2009. — С. 192. — ISBN 978-5-8459-1524-5
Wikimedia Foundation. 2010.
