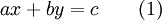- Диофантовы уравнения
-
Диофа́нтово уравнение или уравнение в целых числах — это уравнение с целыми коэффициентами и неизвестными, которые могут принимать только целые значения. Названы в честь древнегреческого математика Диофанта.
Содержание
Линейные диофантовы уравнения
Общий вид линейного диофантова уравнения:
 . В литературе под диофантовыми уравнениями иногда понимаются также уравнения более частного вида — с двумя неизвестными:
. В литературе под диофантовыми уравнениями иногда понимаются также уравнения более частного вида — с двумя неизвестными:которые достаточно хорошо изучены.
Если
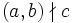 (то есть c не делится нацело на НОД
(то есть c не делится нацело на НОД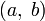 ), то уравнение (1) не разрешимо в целых числах. В самом деле, в этом случае
), то уравнение (1) не разрешимо в целых числах. В самом деле, в этом случае 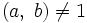 , но тогда число, стоящее слева в (1) делится на
, но тогда число, стоящее слева в (1) делится на 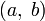 , а стоящее справа — нет. Если в уравнении ax + by = 1
, а стоящее справа — нет. Если в уравнении ax + by = 1 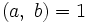 , то оно разрешимо в целых числах.
, то оно разрешимо в целых числах.Пусть
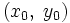 — решение уравнения ax + by = c. Тогда все его решения находятся по следующим формулам:
— решение уравнения ax + by = c. Тогда все его решения находятся по следующим формулам:- x = x0 − bn, y = y0 + an,
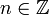 .
.
Начальное (базисное) решение
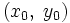 можно построить таким образом. Если
можно построить таким образом. Если 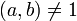 , то (если уравнение имеет решения) c делится на (a, b) в силу вышесказанного. Тогда уравнение сводится к виду a1x + b1y = c1 путем деления всех коэффициентов на (a,b). Для уравнения ax + by = c с (a,b) = 1 базисное решение получается из соотношения Безу для a, b:
, то (если уравнение имеет решения) c делится на (a, b) в силу вышесказанного. Тогда уравнение сводится к виду a1x + b1y = c1 путем деления всех коэффициентов на (a,b). Для уравнения ax + by = c с (a,b) = 1 базисное решение получается из соотношения Безу для a, b:- ua + vb = 1,
исходя из которого, можно положить
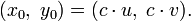
Некоторые другие уравнения
- xn + yn = zn:
- При n = 2 решениями этого уравнения являются пифагоровы тройки
- Великая теорема Ферма утверждает, что это уравнение не имеет положительных целых решений при n > 2.
- x2 − ny2 = 1, где n не является точным квадратом — уравнение Пелля
- xz − yt = 1, где z,t > 1, — уравнение Каталана
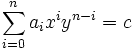 при
при 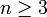 и
и 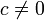 — уравнения Туэ
— уравнения Туэ
Неразрешимость в общем виде
Десятая проблема Гильберта, сформулированная в 1900 г., состоит в нахождении алгоритма решения произвольных диофантовых уравнений. В 1970 г. Юрий Матиясевич доказал алгоритмическую неразрешимость этой проблемы.
См. также
- Гельфонд А.О. Решение уравнений в целых числах. — М.: Наука, 1978. — (Популярные лекции по математике).
- В. Н. Серпинский О решении уравнений в целых числах. — М.: Физматлит, 1961. — 88 с.
Wikimedia Foundation. 2010.