- Упаковка шаров
-
Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей.
 Размещение плодов апельсина
Размещение плодов апельсина
Упаковка шаров[1] — это задача о размещении не пересекающихся одинаковых шаров в Евклидовом пространстве. Типичная постановка задачи звучит так: найти способ расположения шаров в пространстве, при котором покрыта наибольшая доля этого пространства.
Содержание
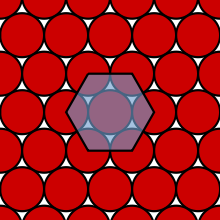
Упаковка кругов на плоскости
 Наиболее эффективный способ упаковать круги разного размера не так уж очевиден
Наиболее эффективный способ упаковать круги разного размера не так уж очевиден
В двумерном Евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки
В 1940 году было доказано, что данная упаковка является самой плотной.
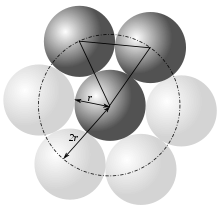
Конфигурации плотной упаковки шаров
Гранецентрированная кубическая упаковка
Этот раздел статьи ещё не написан. Согласно замыслу одного из участников Википедии, на этом месте должен располагаться специальный раздел.
Вы можете помочь проекту, написав этот раздел.Слоёная решётчатая упаковка L3
Гексагональная плотная упаковка (нерешётчатая)
Решётка Лича
См. также
- Контактное число — сколько одинаковых шаров можно расположить вокруг одного такого же центрального шара, чтобы все они касались его.
- Задача о редчайшем покрытии — как наиболее экономно расположить одинаковые шары в пространстве, чтобы каждая точка пространства оказалась внутри или на границе хотя бы одного из них? (В отличие от задачи о плотнейшей упаковке (неперекрывающихся шаров), здесь шары обязательно перекрываются.)
- Алгоритм Любачевского — Стилинжера эвристически находит плотные упаковки шаров и кругов, причём эти упаковки часто оказываются оптимальными.
- Сингония
- Параллелоэдр
Примечания
- ↑ 1 2 Слоэн Н. Дж. А. Упаковка шаров // В мире науки. — 1984. — № 3. — С. 72-82.
Ссылки
- Упаковка шаров
- Д. К. Новая головоломка: укладывание шариков в куб // Квант. — 1990. — № 5. — С. 82.
Категории:- Комбинаторная геометрия
- Упаковка
Wikimedia Foundation. 2010.