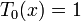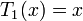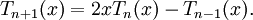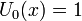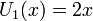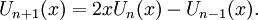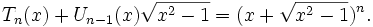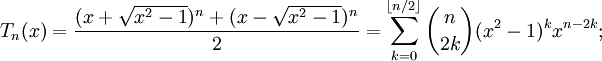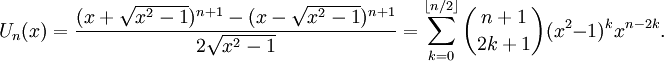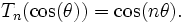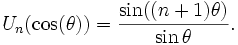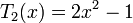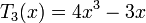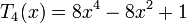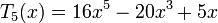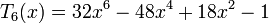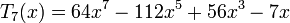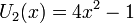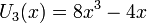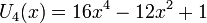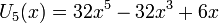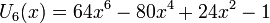Полином Чебышева

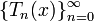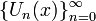Многочле́ны Чебышёва — две последовательности многочленов $\{ T_n(x)\}_{n=0}^{\infty}$ и $\{ U_n(x)\}_{n=0}^{\infty}$, названные в честь их первооткрывателя Пафнутия Львовича Чебышёва.

T₁, T₂, T₃, T₄, T₅

Многочлен Чебышёва первого рода T_n(x) характеризуется как многочлен степени n со старшим коэффициентом 2^{n - 1}, который меньше всего отклоняется от нуля на интервале [ − 1,1].

U₁, U₂, U₃, U₄, U₅

Многочлен Чебышёва второго рода U_n(x) характеризуется как многочлен степени n со старшим коэффициентом 2ⁿ, интеграл от абсолютной величины которого по интервалу [ − 1,1] принимает наименьшее возможное значение.

Рекурсивное определение

Многочлены Чебышёва первого рода T_n(x) могут быть определены с помощью рекуррентного соотношения:

$T_0(x) = 1 \,$

$T_1(x) = x \,$

$T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x). \,$

Многочлены Чебышёва второго рода U_n(x) могут быть определены с помощью рекуррентного соотношения:

$U_0(x) = 1 \,$

$U_1(x) = 2x \,$

$U_{n+1}(x) = 2xU_n(x) - U_{n-1}(x). \,$

Явные формулы

Многочлены Чебышёва являются решениями уравнения Пелля:

T_n(x)² − (x² − 1)U_{n − 1}(x)² = 1

в кольце многочленов с вещественными коэффициентами и удовлетворяют тождеству:

$T_n(x) + U_{n-1}(x)\sqrt{x^2-1} = (x + \sqrt{x^2-1})^n.$

Из последнего тождества также следуют явные формулы:

$T_n(x)=\frac{(x+\sqrt{x^2-1})^n+(x-\sqrt{x^2-1})^n}{2} = \sum_{k=0}^{\lfloor n/2\rfloor} \binom{n}{2k} (x^2-1)^k x^{n-2k};$

$U_n(x)=\frac{(x+\sqrt{x^2-1})^{n+1}-(x-\sqrt{x^2-1})^{n+1}}{2\sqrt{x^2-1}} = \sum_{k=0}^{\lfloor n/2\rfloor} \binom{n+1}{2k+1} (x^2-1)^k x^{n-2k}.$

Тригонометрическое определение

Многочлены Чебышёва первого рода T_n(x) могут быть также определены с помощью равенства:

$T_n(\cos(\theta))=\cos(n\theta). \,$

или, что почти эквивалентно,

T_n(z) = cos(narccosz)

Многочлены Чебышёва второго рода U_n(x) могут быть также определены с помощью равенства:

$U_n(\cos(\theta)) = \frac{\sin((n+1)\theta)}{\sin\theta}.$

Примеры

Несколько первых многочленов Чебышёва первого рода

$T_0(x) = 1 \,$

$T_1(x) = x \,$

$T_2(x) = 2x^2 - 1 \,$

$T_3(x) = 4x^3 - 3x \,$

$T_4(x) = 8x^4 - 8x^2 + 1 \,$

$T_5(x) = 16x^5 - 20x^3 + 5x \,$

$T_6(x) = 32x^6 - 48x^4 + 18x^2 - 1 \,$

$T_7(x) = 64x^7 - 112x^5 + 56x^3 - 7x \,$

Несколько первых многочленов Чебышёва второго рода

$U_0(x) = 1 \,$

$U_1(x) = 2x \,$

$U_2(x) = 4x^2 - 1 \,$

$U_3(x) = 8x^3 - 4x \,$

$U_4(x) = 16x^4 - 12x^2 + 1 \,$

$U_5(x) = 32x^5 - 32x^3 + 6x \,$

$U_6(x) = 64x^6 - 80x^4 + 24x^2 - 1 \,$

Свойства

Многочлены Чебышёва обладают следующими свойствами:

• Ортогональность по отношению к соответствующим скалярному произведению (с весом 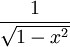$\frac1\sqrt{1-x^2}$ для многочленов первого рода и 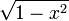$\sqrt{1-x^2}$ для многочленов второго рода).
• Среди всех многочленов, значения которых на отрезке [ − 1,1] не превосходят по модулю 1, многочлен Чебышёва имеет:
  • наибольший старший коэффициент
  • наибольшее значение в любой точке $a \geq 1$
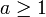
• Нули полинома Чебышёва являются оптимальными узлами в различных интерполяционных схемах.

Обобщения

Вопрос о многочленах минимальной нормы с фиксированными коэффициентами при двух старших степенях был рассмотрен позднее Золотарёвым, найденные им полиномы носят название многочлены Золотарёва.

См. также

• многочлены Фабера

Ссылки

• Васильев Н., Зелевинский А., Многочлены Чебышёва и рекуррентные соотношения, Квант, № 1, 1982.