Рекурсия

У этого термина существуют и другие значения, см. Рекурсия (значения).

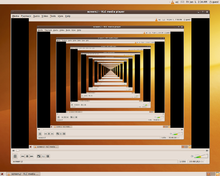
Визуальная форма рекурсии (эффект Дросте)

Рекурсивное изображение экрана

Визуальная форма рекурсии страницы Википедии

Реку́рсия — процесс повторения элементов самоподобным образом. Например, если два зеркала установить друг напротив друга, то возникающие в них вложенные отражения суть одна из форм бесконечной рекурсии.

Термин «рекурсия» используется в различных специальных областях знаний — от лингвистики до логики, но наиболее широкое применение находит в математике и информатике. В математике и информатике рекурсия имеет отношение к методу определения функций: рекурсивно заданная функция в своём определении содержит себя, в частности, рекурсивной является функция, заданная рекуррентной формулой. Таким образом, можно одним выражением дать бесконечный набор способов вычисления функции, определить множество объектов через самого себя с использованием ранее заданных частных определений.

С рекурсией тесно связана математическая индукция: она является естественным способом доказательства свойств функций на натуральных числах, рекурсивно заданных через свои меньшие значения.

В математике

Треугольник Серпинского

• Метод Гаусса — Жордана для решения систем линейных алгебраических уравнений является рекурсивным.
• Факториал целого неотрицательного числа n (обозначается $n!$) определяется как

  $n!=n\cdot(n-1)!$ при $n>0$ и $n!=1$ при $n=0$

• Числа Фибоначчи определяются с помощью рекуррентного соотношения:

  Первое и второе числа Фибоначчи равны 1

  Для $n>2$, $n$-e число Фибоначчи равно сумме $(n-1)$-го и $(n-2)$-го чисел Фибоначчи

• Практически все геометрические фракталы задаются в форме бесконечной рекурсии (например, треугольник Серпинского).

В программировании

Функции

Блок схема рекурсивного алгоритма решения Ханойской башни.

В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная или косвенная рекурсия), например, функция $A$ вызывает функцию $B$, а функция $B$ — функцию $A$. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за счёт этого работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения.

Любую рекурсивную функцию можно заменить циклом и стеком.

См. также: Примеры реализации функции факториал в Викиучебнике

Данные

Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):

 struct element_of_list
 {
   element_of_list *next; /* ссылка на следующий элемент того же типа */
   int data; /* некие данные */
 };

Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.

В физике

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из уменьшающихся отражений зеркал.

Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.

В лингвистике

См. также: Рекурсия (лингвистика)

Способность языка порождать вложенные предложения и конструкции. Базовое предложение «кошка съела мышь» может быть за счёт рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку. Однако, в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Дэниэл Эверетт (англ.)^[1].

В культуре

См. также: Mise en abyme и Эффект Дросте

Большая часть шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода, например, известно высказывание: «чтобы понять рекурсию, нужно сначала понять рекурсию».

Весьма популярна шутка о рекурсии, напоминающая словарную статью:

рекурсия 

см. рекурсия

Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:

• рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки»:

Нашёл следующие краткие сведения:
«СЕПУЛЬКИ — важный элемент цивилизации ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКАРИИ».
Я последовал этому совету и прочёл:
«СЕПУЛЬКАРИИ — устройства для сепуления (см.)».
Я поискал «Сепуление»; там значилось:
«СЕПУЛЕНИЕ — занятие ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКИ».

Лем С. «Звёздные дневники Ийона Тихого. Путешествие четырнадцатое.»

• Рассказ из «Кибериады» о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).
• Рекурсивные акронимы: GNU (GNU Not Unix), PHP (PHP: Hypertext Preprocessor) и т. д.

См. также

• Математическая индукция
• Корекурсия
• Рекуррентная формула
• Возвратная последовательность
• Докучная сказка
• Рефлексивное отношение
• Порочный круг

Примечания

1. ↑ О рекурсии в лингвистике, её разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е. А. Лодатко «Рекурсивные лингвистические структуры»

Имеется викиучебник по теме
«Рекурсия»