ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА

- формула для приближенного вычисления значений функции f(x), основанного на замене приближаемой функции f(x)более простой в каком-то смысле функцией

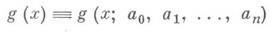
наперед заданного класса, причем параметры a_i, i=0, 1, ..., п, выбираются таким образом, чтобы значения g(x)совпадали с известными заранее значениями f(x)для данного множества ге+1 попарно различных значений аргумента:

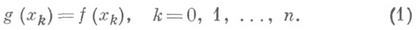
Такой способ приближенного представления функций наз. интерполированием, или интерполяцией, а точки x_k, для к-рых должны выполняться условия (1),- узлами интерполяции. Вместо простейших условий (1) могут быть заданы значения каких-либо иных величин, связанных с f(x), напр, значения производных функции f(x)в узлах интерполяции.

Среди методов интерполирования самым распространенным является линейное интерполирование, когда приближение ищется в классе (обобщенных) полиномов

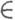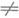по некоторой системе функций j₀(x),j₁(x), ..., j_n(x). Для того, чтобы для любой функции f(х), определенной на отрезке [а, b], и для любого набора n+1 узлов х ₀, х ₁,. .., х _п, х _i[a, b], x_ix_j при ijсуществовал интерполяционный полином (2), необходимо и достаточно, чтобы система функций {j_i (х)}являлась Чебышева системой на отрезке [ а, b]. При этом интерполяционный полином будет единственным и его коэффициенты а;можно найти непосредственным решением системы (1).

Чаще всего в качестве {j_i(x)}берут последовательность степеней х:

последовательность тригонометрических функций:

1, sin х,cos x,sin 2x,cos 2x, ..., или последовательность показательных функций

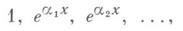
где {а,} - некоторая подпоследовательность попарно различных действительных чисел.

В случае интерполирования алгебраич. многочленами

система функций {j_i (х)}такова:

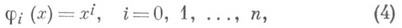
а система уравнений (1) имеет вид

Система (4) является системой Чебышева, что обеспечивает существование и единственность интерполяционного многочлена вида (3). Особенностью системы (4) является возможность получения явного представления интерполяционного многочлена (3), не прибегая к непосредственному решению системы (5). Одну из явных форм интерполяционного многочлена (3):

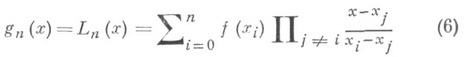
наз. интерполяционным многочленом Лагранжа. В предположении непрерывности производной fⁿ⁺¹(x) остаточный член интерполяционного многочлена (6) может быть записан в форме

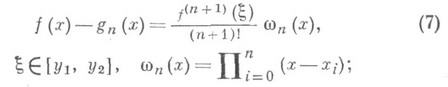
здесь y₁=min ( х ₀, х ₁,.. .,х _п, х), y₂ = mах(х ₀, х ₁, . .., х _п, х). Величина остаточного члена (7) зависит, в частности, от значения многочлена w_n (х). Представляет интерес такой выбор узлов интерполяции, при к-ром sup|w_n (х)|

был наименьшим. Распределение узлов будет оптимальным в указанном смысле, если в качестве узлов интерполяции взяты корни

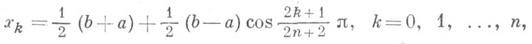
наименее уклоняющегося от нуля на отрезке [ а, b]многочлена

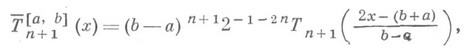
где T_n+1(z)- Чебышева многочлен степени n+1.

Существует ряд других явных представлений интерполяционного алгебраич. многочлена (3), более приспособленных для решения тех или иных практич. задач интерполяции (см., напр., Бесселя интерполяционная формула, Гаусса интерполяционная формула, Ньютона интерполяционная формула, Стирлинга интерполяционная формула, Стеффенсена интерполяционная формула, Эверетта интерполяционная формула). Если заранее трудно оценить степень интерполяционного многочлена, требуемую для достижения заданной точности (напр., при интерполировании таблиц), то прибегают к использованию Эйткена схемы, по к-рой интерполяционные многочлены все более высокой степени строятся последовательно, что позволяет контролировать точность в процессе вычислений. Другой подход к построению И. ф. см. в ст. Фрезера диаграмма.

Решение задачи алгебраич. интерполирования по значениям функции и ее производных в узлах интерполяции дается Эрмита интерполяционной формулой.

Лит.:[1] Березин И. С, Жидков Н. П., Методы вычислений, 3 изд., т. 1, М., 1966; [2] Бахвалов Н. С., Численные методы, 2 изд., М., 1975.

М. К. Самарин.