Открытое множество (топология)
- Открытое множество (топология)
-
Откры́тое мно́жество в математическом анализе, геометрии — это множество, каждая точка которого входит в него вместе с некоторой окрестностью. Открытое множество также является фундаментальным понятием общей топологии.
Термин «открытое множество» применяется к подмножествам топологических пространств и никак не характеризует «само» множество (ни в смысле теории множеств, ни даже в смысле индуцированной на нём топологической структуры). [1] [2]
Евклидово пространство
Пусть 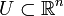 есть некоторое подмножество евклидова пространства. Тогда U называется открытым, если
есть некоторое подмножество евклидова пространства. Тогда U называется открытым, если 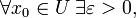 такое что
такое что 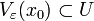 , где
, где 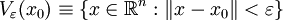 — ε-окрестность точки x0. Иными словами, множество открыто, если любая его точка является внутренней.
— ε-окрестность точки x0. Иными словами, множество открыто, если любая его точка является внутренней.
Например, промежуток как подмножество действительной прямой является открытым множеством.
Метрическое пространство
Пусть (X,ρ) — некоторое метрическое пространство, и 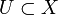 . Тогда U называется открытым, если
. Тогда U называется открытым, если 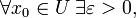 такое что
такое что 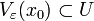 , где
, где 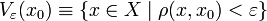 — ε-окрестность точки x0 относительно метрики ρ.
— ε-окрестность точки x0 относительно метрики ρ.
Топологическое пространство
Обобщением приведённых выше определений является понятие открытого множества из общей топологии.
Топологическое пространство 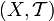 по определению содержит «перечень» своих открытых подмножеств
по определению содержит «перечень» своих открытых подмножеств 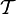 — «топологию», определённую на X. Подмножество
— «топологию», определённую на X. Подмножество 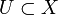 , такое, что оно является элементом топологии (то есть
, такое, что оно является элементом топологии (то есть 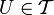 ), называется открытым множеством относительно топологии
), называется открытым множеством относительно топологии 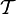 .
.
См. также
Сноски
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Открытое множество (топология)" в других словарях:
Открытое множество — это множество, каждый элемент которого входит в него вместе с некоторой окрестностью. Открытое множество является фундаментальным понятием общей топологии. Термин «открытое множество» применяется к подмножествам топологических пространств и никак … Википедия
ОТКРЫТОЕ МНОЖЕСТВО — топологического пространства элемент топологии этого пространства. Подробнее, пусть топология t топологич. пространства (X, t) определяется как такая система т подмножеств множества X, что: 1) 2) если i=l, 2, то , 3) если , то ; тогда открытыми… … Математическая энциклопедия
Топология — (от греч. tоpos место и …логия (См. ...Логия) часть геометрии, посвященная изучению феномена непрерывности (выражающегося, например, в понятии предела). Разнообразие проявлений непрерывности в математике и широкий спектр различных… … Большая советская энциклопедия
Открытое отображение — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
ТОПОЛОГИЯ — в широком смысле область математики, изучающая топологич. свойства разл. матем. и физ. объектов. Интуитивно, к топологич. относятся качественные, устойчивые свойства, не меняющиеся при деформациях. Матем. формализация идеи о топологич. свойствах… … Физическая энциклопедия
ТОПОЛОГИЯ — раздел математики, занимающийся изучением свойств фигур (или пространств), которые сохраняются при непрерывных деформациях, таких, например, как растяжение, сжатие или изгибание. Непрерывная деформация это деформация фигуры, при которой не… … Энциклопедия Кольера
Открытое покрытие — Покрытие в математике это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии. Содержание 1 Определения 2 Связанные определения 3 Свойства … Википедия
Дискетная топология — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
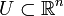 есть некоторое подмножество евклидова пространства. Тогда U называется открытым, если
есть некоторое подмножество евклидова пространства. Тогда U называется открытым, если 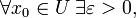 такое что
такое что 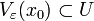 , где
, где 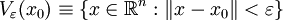 — ε-окрестность точки x0. Иными словами, множество открыто, если любая его точка является внутренней.
— ε-окрестность точки x0. Иными словами, множество открыто, если любая его точка является внутренней.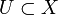 . Тогда U называется открытым, если
. Тогда U называется открытым, если 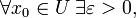 такое что
такое что 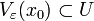 , где
, где 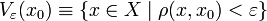 — ε-окрестность точки x0 относительно метрики ρ.
— ε-окрестность точки x0 относительно метрики ρ.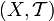 по определению содержит «перечень» своих открытых подмножеств
по определению содержит «перечень» своих открытых подмножеств 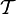 — «топологию», определённую на X. Подмножество
— «топологию», определённую на X. Подмножество 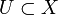 , такое, что оно является элементом топологии (то есть
, такое, что оно является элементом топологии (то есть 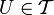 ), называется открытым множеством относительно топологии
), называется открытым множеством относительно топологии 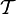 .
.