- ТОПОЛОГИЯ
- ТОПОЛОГИЯ
-
- в широком смысле область математики, изучающая топологич. свойства разл. матем. и физ. объектов. Интуитивно, к топологич. относятся качественные, устойчивые свойства, не меняющиеся при деформациях.
Матем. формализация идеи о топологич. свойствах обычно основывается на понятии непрерывности. Наиб. универсальным является определение непрерывности, базирующееся на введении T. (в узком смысле слова), или структуры т о п о л о г и ч е с к о г о п р о с т р а н с т в а (коротко - "пространства") в данное множество.T. на произвольном множестве точек X задана, если указано, какие подмножества в X считаются о т к р ы т ы м и (т. е. состоящими только из своих внутр. точек - точек, имеющих окрестности, целиком содержащиеся в данном подмножестве). При этом, по определению, объединение любого числа открытых подмножеств и пересечения конечного их числа должны быть открытым подмножеством, всё множество X и пустое подмножество также считаются открытыми. Дополнение к открытому подмножеству в X наз. з а м кн у т ы м п о д м н о ж е с т в о м. Обычно для задания T. в X указывают её базу: совокупность таких открытых подмножеств, из к-рых любое открытое может быть получено операциями объединения и конечного пересечения. Напр., стандартная T. числовой прямой
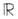 задаётся базой из интервалов a<t<b. Любая часть (подмножество) M топологич. пространства X также наделяется Т.: открытыми в M являются пересечения с M множеств, открытых в X. Напр., в единичном отрезке числовой прямой,
задаётся базой из интервалов a<t<b. Любая часть (подмножество) M топологич. пространства X также наделяется Т.: открытыми в M являются пересечения с M множеств, открытых в X. Напр., в единичном отрезке числовой прямой, 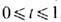 , открытыми будут интервалы a<t<b, полуинтервалы
, открытыми будут интервалы a<t<b, полуинтервалы 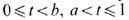 и их любые объединения.
и их любые объединения.
Наиб. важными для приложений классами топологич. пространств являются достаточно общие геом. фигуры - многообразия и комплексы, определения к-рых будут даны ниже, а также функциональные пространства, где точка - это ф-ция (или отображение).
Для топологич. пространств определён ряд след. простейших топологич. понятий, фактически возникающих в элементарной теории ф-ций.
1. Отображение
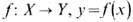 топологич. пространств наз. н е п р е р ы в н ы м, если полный прообраз любого открытого подмножества в Y открыт в X. В частности, непрерывные отображения пространства X в числовую прямую наз. непрерывными ф-циями на X.
топологич. пространств наз. н е п р е р ы в н ы м, если полный прообраз любого открытого подмножества в Y открыт в X. В частности, непрерывные отображения пространства X в числовую прямую наз. непрерывными ф-циями на X.
2. Два пространства X, Y наз. т о п о л о г и ч е с к и э кв и в а л е н т н ы м и, если определены два непрерывных взаимно обратных отображения (г о м е о м о р ф и з м а)
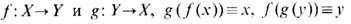 По определению, все топологич. свойства топологически эквивалентных пространств должны совпадать. Числовые (или более сложные, алгебраические) характеристики топологич. свойств, называемые т о п о л о г и ч е с к и м и и н в а р и а нт а м и, также должны быть одинаковыми для топологически эквивалентных пространств. Важным (напр., в качественной теории динамических систем )примером такого топологич. инварианта, определённого для широкого класса пространств, является р а з м е р н о с т ь (разл. варианты её определения см. [5 ]).
По определению, все топологич. свойства топологически эквивалентных пространств должны совпадать. Числовые (или более сложные, алгебраические) характеристики топологич. свойств, называемые т о п о л о г и ч е с к и м и и н в а р и а нт а м и, также должны быть одинаковыми для топологически эквивалентных пространств. Важным (напр., в качественной теории динамических систем )примером такого топологич. инварианта, определённого для широкого класса пространств, является р а з м е р н о с т ь (разл. варианты её определения см. [5 ]).
3. Непрерывное отображение
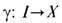 единичного отрезка I в пространство X наз. п у т ё м, соединяющим его концы - точки g(0) и g(1). Пространство X наз. (линейно) с в я з н ы м, если любые две его точки можно соединить путём. Если пространство X не является связным, то оно распадается на куски - к о м п о н е н т ы с в я з н о с т и, каждая из к-рых связна.
единичного отрезка I в пространство X наз. п у т ё м, соединяющим его концы - точки g(0) и g(1). Пространство X наз. (линейно) с в я з н ы м, если любые две его точки можно соединить путём. Если пространство X не является связным, то оно распадается на куски - к о м п о н е н т ы с в я з н о с т и, каждая из к-рых связна.
4. П р я м о е п р о и з в е д е н и е Xx Y пространств X, Y определяется как множество пар ( х, у )точек из X, Y, причём прямые произведения открытых подмножеств в X, Y образуют базу в XxY Напр., прямое произведение
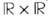 числовых прямых-это плоскость; непрерывные ф-ции на
числовых прямых-это плоскость; непрерывные ф-ции на 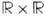 -это непрерывные ф-ции двух переменных.
-это непрерывные ф-ции двух переменных.
5. Д е ф о р м а ц и я, или г о м о т о п и я, отображения
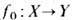 - это непрерывное отображение
- это непрерывное отображение 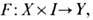 y=F(x, t), прямого произведения пространства X на единичный отрезок
y=F(x, t), прямого произведения пространства X на единичный отрезок 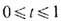 такое, что
такое, что 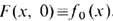 . Отображение
. Отображение  заданное ф-лой
заданное ф-лой 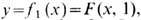 будет результатом деформации отображения f0. Отображения f0 и f1 наз. г о м о т о п н ы м и. Все отображения из X в Y (поля на X со значениями в Y )распадаются на классы гомотопных отображений. Числовые характеристики таких классов наз. г о м о т о п и ч е с к и м и и н в а р иа н т а м и отображений или т о п о л о г и ч е с к и м и з а р я д а м и.
будет результатом деформации отображения f0. Отображения f0 и f1 наз. г о м о т о п н ы м и. Все отображения из X в Y (поля на X со значениями в Y )распадаются на классы гомотопных отображений. Числовые характеристики таких классов наз. г о м о т о п и ч е с к и м и и н в а р иа н т а м и отображений или т о п о л о г и ч е с к и м и з а р я д а м и.
6. Два пространства X, Y наз. г о м о т о п и ч е с к и э кв и в а л е н т н ы м и, если определены непрерывные отображения:
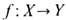 и
и 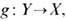 такие, что отображение g(f(x)) гомотопно тождественному отображению
такие, что отображение g(f(x)) гомотопно тождественному отображению 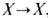 , а отображение f(g(x))- тождественному отображению
, а отображение f(g(x))- тождественному отображению 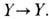 Напр., евклидово пространство (или выпуклая область в нём) с т я г и в а е м о, т. е. гомотопически эквивалентно точке. Многие важные топологич. инварианты (гомологии, гомотопич. группы, см. ниже) одинаковы для гомотопически эквивалентных пространств, т. е. являются г о м о т оп и ч е с к и м и и н в а р и а н т а м и.
Напр., евклидово пространство (или выпуклая область в нём) с т я г и в а е м о, т. е. гомотопически эквивалентно точке. Многие важные топологич. инварианты (гомологии, гомотопич. группы, см. ниже) одинаковы для гомотопически эквивалентных пространств, т. е. являются г о м о т оп и ч е с к и м и и н в а р и а н т а м и.
7. Выделен важный подкласс х а у с д о р ф о в ы х п р ос т р а н с т в, в к-рых любые две точки можно окружить непересекающимися открытыми подмножествами (неха-усдорфовы пространства, как правило, не возникают в приложениях). В частности, хаусдорфовыми являются м е т р и ч е с к и е п р о с т р а н с т в а, в к-рых T. определяется метрикой: неотрицательной ф-цией r( х, у), задающей расстояние между любыми двумя точками х, у пространства [требуется, чтобы r(x,y)=0 только при у = х;
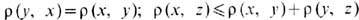 - неравенство треугольника]. T. в метрич. пространстве определяется базой из открытых шаров
- неравенство треугольника]. T. в метрич. пространстве определяется базой из открытых шаров 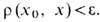 Класс к о мп а к т н ы х п р о с т р а н с т в X определяется след. условием: из любого покрытия пространства X бесконечным числом открытых подмножеств можно выделить конечное число подмножеств, также покрывающих X. Непрерывные ф-ции на компактном связном пространстве обладают многими свойствами ф-ций, непрерывных на отрезке (ограниченность и др.). В евклидовом пространстве компактными будут замкнутые ограниченные подмножества.
Класс к о мп а к т н ы х п р о с т р а н с т в X определяется след. условием: из любого покрытия пространства X бесконечным числом открытых подмножеств можно выделить конечное число подмножеств, также покрывающих X. Непрерывные ф-ции на компактном связном пространстве обладают многими свойствами ф-ций, непрерывных на отрезке (ограниченность и др.). В евклидовом пространстве компактными будут замкнутые ограниченные подмножества.
Особой наглядностью отличаются топология, конструкции и задачи, возникающие при изучении кривых и поверхностей в трёхмерном пространстве. Единственным тополо-гич. инвариантом поверхности M2 (связной и замкнутой, т. е. без края) является её род, обозначаемый обычно через g, равный числу "дыр" на рисунке поверхности (рис. 1). [Мы не рассматриваем пока неориентируемые поверхности (см. ниже), к-рые нельзя расположить в трёхмерном пространстве без самопересечений.] Для сферы g=0, для тора g=1Если поверхность представлена в виде многогранника, то её род может быть вычислен через э й л е р о в у х а р а к т е р и с т и к у

где В-число вершин, P-число рёбер, а Г-число граней многогранника. Непрерывным вариантом этой ф-лы является ф-ла Гаусса - Бонне

где К- гауссова кривизна поверхности, dS- элемент площади. Если M2 задана как риманова поверхность многозначной алгебраич. ф-ции w = w(z), где
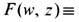
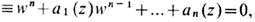 F- многочлен от двух переменных, то её род может быть вычислен по ф-ле Римана - Гурвица, g=r/2-n+1, где r - суммарная кратность точек ветвления (см. Многозначная функция )ф-ции w(z) в к-рых происходит слияние нек-рых ветвей ф-ции w(z) [если в точке ветвления z0 после слияния остаются различными k ветвей w1(z0) ...,wk(z0), то кратность этой точки ветвления, по определению, равна n-k].
F- многочлен от двух переменных, то её род может быть вычислен по ф-ле Римана - Гурвица, g=r/2-n+1, где r - суммарная кратность точек ветвления (см. Многозначная функция )ф-ции w(z) в к-рых происходит слияние нек-рых ветвей ф-ции w(z) [если в точке ветвления z0 после слияния остаются различными k ветвей w1(z0) ...,wk(z0), то кратность этой точки ветвления, по определению, равна n-k].
Единственный топологич. инвариант h замкнутых н е о р и е н т и р у е м ы х п о в е р х н о с т е й определяется исходя из следующей их явной конструкции: нужно вырезать в поверхности сферы h отверстий и заклеить каждое из них листом Мёбиуса (важно, что его границей является окружность, рис. 2). При h =1 получается проективная плоскость, при h=2 - бутылка Клейна (рис. 3). Эйлерова характеристика такой поверхности, определяемая по аналогии с (1), равна 2-h. Такие поверхности в трёхмерном пространстве обязательно имеют самопересечения.
Рассмотрим теперь примеры топологич. задач теории кривых. Замкнутая (гладкая) несамопересекающаяся кривая g на плоскости всегда расположена "топологически одинаково": она разделяет плоскость на две части-внутреннюю и внешнюю. Первые примеры топологич. величин возникают в теории ф-ций комплексного переменного: если замкнутая кривая g лежит в области U на плоскости и ф-ция f(z) комплексно-аналитична в U, то величина
 не меняется при деформациях g внутри области U.
не меняется при деформациях g внутри области U.
Для з а ц е п л е н и й-двух несамопересекающихся и непересекающих друг друга замкнутых кривых в трёхмерном пространстве - определён топологич. инвариант их расположения- к о э ф ф и ц и е н т з а ц е п л е н и я {g1, g2}. Он равен числу витков одной кривой вокруг другой и не меняется при деформациях кривых, в процессе к-рых не происходит пересечений. Для незацепленных кривых, к-рые указанными деформациями можно растащить по разные стороны нек-рой плоскости, коэф. зацепления равен нулю. Коэф. зацепления замкнутых кривых r = r1(t), r=r2(t'0 вычисляется по ф-ле
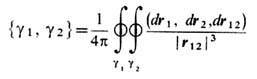
[r12=r1(t)-r2(t'), в числителе - смешанное произведение]. Однако коэф. зацепления не несёт всей топологич. информации о взаимном расположении двух замкнутых кривых; напр., для зацепленных кривых, изображённых на рис. 4, коэф. зацепления равен нулю.
Более сложно строятся топологич. инварианты узлов- несамопересекающихся замкнутых кривых в трёхмерном пространстве
 (или в трёхмерной сфере S3, получающейся добавлением к
(или в трёхмерной сфере S3, получающейся добавлением к  бесконечно удалённой точки). Два узла топологически эквивалентны, если один из них можно продеформировать в другой, причём в процессе деформации не должно возникать самопересечений. Полным топологич. инвариантом, измеряющим отличие узла от тривиального (рис. 5), является группа узла, совпадающая с фундам. группой (см. ниже) дополнения к узлу в S3. (Для тривиального узла она совпадает с группой целых чисел.) Однако ввиду некоммутативности группы узла (алгоритм её вычисления см. в [2]) этот инвариант непригоден, в частности для эфф. топологич. классификации узлов. Определены также более грубые инварианты узлов и зацеплений-многочлены Александера, Джонса и др., возникающие как статистич. суммы в нек-рых моделях двумерной статистич. физики. Узлы и зацепления могут быть получены посредством нек-рых отождествлений в группах кос; это позволяет строить топологич. инварианты узлов и зацеплений с помощью теории представлений групп кос, основывающейся на использовании теории R -матриц. Предпринимались попытки использования узлов и зацеплений в статистич. механике нек-рых веществ с длинными молекулами.
бесконечно удалённой точки). Два узла топологически эквивалентны, если один из них можно продеформировать в другой, причём в процессе деформации не должно возникать самопересечений. Полным топологич. инвариантом, измеряющим отличие узла от тривиального (рис. 5), является группа узла, совпадающая с фундам. группой (см. ниже) дополнения к узлу в S3. (Для тривиального узла она совпадает с группой целых чисел.) Однако ввиду некоммутативности группы узла (алгоритм её вычисления см. в [2]) этот инвариант непригоден, в частности для эфф. топологич. классификации узлов. Определены также более грубые инварианты узлов и зацеплений-многочлены Александера, Джонса и др., возникающие как статистич. суммы в нек-рых моделях двумерной статистич. физики. Узлы и зацепления могут быть получены посредством нек-рых отождествлений в группах кос; это позволяет строить топологич. инварианты узлов и зацеплений с помощью теории представлений групп кос, основывающейся на использовании теории R -матриц. Предпринимались попытки использования узлов и зацеплений в статистич. механике нек-рых веществ с длинными молекулами.
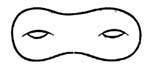
Рис. 1. Поверхность рода g=2.

Рис. 2. Лист Мёбиуса.
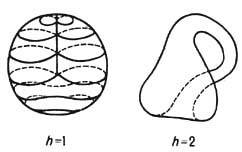
Рис. 3. Неориентируемые поверхности.
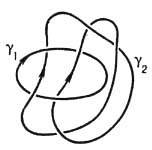
Рис. 4. Пример зацепленных кривых с коэффициентом зацепления, равным нулю.
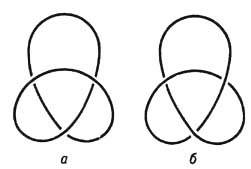
Рис. 5. Тривиальный ( а) и нетривиальный ( б )узлы.
Многомерные обобщения большинства перечисленных наглядно-топологич. задач приводят к T, многообразий - важнейшему разделу Т., тесно взаимодействующему с совр. матем. физикой. Множество точек Mn является n -мерным гладким многообразием, если оно представлено в виде объединения нек-рых своих подмножеств Ua, a=1, 2, ...- карт, каждое из к-рых отождествлено с областью (открытым подмножеством) в пространстве
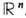 . Отображения отождествления
. Отображения отождествления  задают в каждом Ua локальные координаты. Требуется, чтобы на пересечении двух карт Ua и Ub координаты
задают в каждом Ua локальные координаты. Требуется, чтобы на пересечении двух карт Ua и Ub координаты 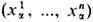 выражались через координаты
выражались через координаты  (и обратно) при помощи гладких (т. е. непрерывно дифференцируемых достаточное число раз) ф у н к ц и й п е р е х о д а:
(и обратно) при помощи гладких (т. е. непрерывно дифференцируемых достаточное число раз) ф у н к ц и й п е р е х о д а:
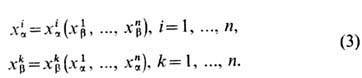
T. в многообразии определяется так: подмножество в M " открыто, если открыто его пересечение с каждой картой. Дополнительно в определении многообразия требуется, чтобы пересечение любых двух карт было открыто, а также чтобы Mn было хаусдорфовым топологич. пространством. Многообразие наз. з а м к н у т ы м, если оно компактно и связно. Все понятия дифференц. исчисления ф-ций многих переменных и локальной дифференц. геометрии (гладкие ф-ции и отображения, векторные и тензорные поля, дифференц. формы, римановы метрики и др.) несложно переносятся на многообразия. Многообразия
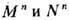 наз. д и ф ф е о м о р ф н ы м и, если определены взаимообратные гладкие отображения
наз. д и ф ф е о м о р ф н ы м и, если определены взаимообратные гладкие отображения  и
и 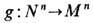 Многообразие Mn- о р и е н т и р о в а н н о е, если локальные координаты согласованы так, что на пересечении двух карт
Многообразие Mn- о р и е н т и р о в а н н о е, если локальные координаты согласованы так, что на пересечении двух карт 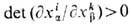 . Если такой согласованный выбор карт на Mn невозможен (напр., на проективной плоскости), то многообразие наз. н е о р и е н т и р у е м ы м. Определён интеграл
. Если такой согласованный выбор карт на Mn невозможен (напр., на проективной плоскости), то многообразие наз. н е о р и е н т и р у е м ы м. Определён интеграл 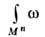 дифференц. n -формы w (см. Дифференциальная форма )по n -мерному замкнутому ориентированному многообразию Mn. М н о г о о б р а з и е с к р а е м Wn выделяется в n -мер-ном замкнутом многообразии неравенством
дифференц. n -формы w (см. Дифференциальная форма )по n -мерному замкнутому ориентированному многообразию Mn. М н о г о о б р а з и е с к р а е м Wn выделяется в n -мер-ном замкнутом многообразии неравенством 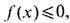 где f(x)- гладкая ф-ция, причём на крае дWn, где f(x) =0, должно выполняться условие
где f(x)- гладкая ф-ция, причём на крае дWn, где f(x) =0, должно выполняться условие 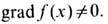 Край дWn ориентированного многообразия сам является ( п-1)-мерным ориентированным многообразием (возможно, несвязным), и для любой дифференциальной ( п-1)-формы w справедлива общая ф-ла Стокса
Край дWn ориентированного многообразия сам является ( п-1)-мерным ориентированным многообразием (возможно, несвязным), и для любой дифференциальной ( п-1)-формы w справедлива общая ф-ла Стокса

где dw-дифференциал формы w (см. Стокса теорема).
Примерами многообразий служат поверхности в многомерных евклидовых пространствах, локально заданные неособыми системами гладких ур-ний. Хотя, в принципе, любое (с нек-рыми топологич. ограничениями, напр., компактное) многообразие может быть задано как поверхность в каком-то многомерном пространстве, ряд многообразий не задаётся в виде поверхностей. Напр., n -мерное проективное пространство RPn определяется как совокупность ненулевых векторов ( u0 : u1 : ... un ), рассматриваемых с точностью до пропорциональности. Карты U0,..., Un определяются из условия
 в карте Ua. Локальные координаты (x1a, х2a, ..., х an )в карте Ua имеют вид xia=
в карте Ua. Локальные координаты (x1a, х2a, ..., х an )в карте Ua имеют вид xia= 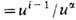 при
при 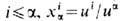 при i>a Ф-ции на RPn - это однородные ф-ции ( п +1) переменных,
при i>a Ф-ции на RPn - это однородные ф-ции ( п +1) переменных, 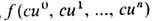 =
= 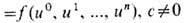 Ещё один класс примеров - n -мер-ный тор Tn, получающийся факторизацией
Ещё один класс примеров - n -мер-ный тор Tn, получающийся факторизацией 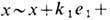
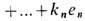 пространства
пространства 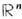 по целочисленной решётке, порождённой произвольным репером e1 ..., е n в
по целочисленной решётке, порождённой произвольным репером e1 ..., е n в 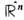 . Ф-ции на Tn - это n -кратно периодические ф-ции п переменных:
. Ф-ции на Tn - это n -кратно периодические ф-ции п переменных: 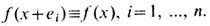 Др. примеры см. в [1 ], [2], [7].
Др. примеры см. в [1 ], [2], [7].
В приложениях часто возникают также многообразия, являющиеся группами Ли и однородными пространствами. Если в определении многообразия п=2 т и ф-ции перехода (3), определённые в области комплексного пространства
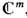 комплексно аналитичны, то М2 т наз. к о м п л е к сн ы м м н о г о о б р а з и е м комплексной размерности т. Примерами комплексно-одномерных многообразий являются комплексная плоскость
комплексно аналитичны, то М2 т наз. к о м п л е к сн ы м м н о г о о б р а з и е м комплексной размерности т. Примерами комплексно-одномерных многообразий являются комплексная плоскость 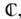 сфера Римана
сфера Римана  получающаяся из
получающаяся из 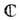 добавлением бесконечно удалённой точки, а также римановы поверхности многозначных аналитических функций. Определены также комплексные проективные пространства CPn, определяемые по аналогии с RPn, но все координаты векторов комплексные. К о м п л е к сн ы е а л г е б р а и ч е с к и е м н о г о о б р а з и я в CPn локально задаются системами однородных алгебраич. ур-ний от координат (u0, u1, ..., и n). Напр., в разл. задачах матем. физики (см. [1], [3]) появляются п о в е р х н о с т и т и п а К 3; представители этого класса поверхностей задаются в CP3 однородными ур-ниями 4-й степени. В интегрируемых системах теории солитонов возникают а б е л е в ы м н о г о о б р а з и я - 2-мерные торы, получающиеся факторизацией пространства
добавлением бесконечно удалённой точки, а также римановы поверхности многозначных аналитических функций. Определены также комплексные проективные пространства CPn, определяемые по аналогии с RPn, но все координаты векторов комплексные. К о м п л е к сн ы е а л г е б р а и ч е с к и е м н о г о о б р а з и я в CPn локально задаются системами однородных алгебраич. ур-ний от координат (u0, u1, ..., и n). Напр., в разл. задачах матем. физики (см. [1], [3]) появляются п о в е р х н о с т и т и п а К 3; представители этого класса поверхностей задаются в CP3 однородными ур-ниями 4-й степени. В интегрируемых системах теории солитонов возникают а б е л е в ы м н о г о о б р а з и я - 2-мерные торы, получающиеся факторизацией пространства 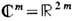 по целочисленной решётке, порождённой векторами e1, ..., е т,
по целочисленной решётке, порождённой векторами e1, ..., е т, 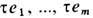 , где e1,..., em - базис в
, где e1,..., em - базис в 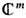 , а t - линейный оператор в пространстве
, а t - линейный оператор в пространстве 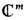 , задаваемый в базисе e1, ..., е т симметрич. матрицей с положительно определённой мнимой частью.
, задаваемый в базисе e1, ..., е т симметрич. матрицей с положительно определённой мнимой частью.
Одной из важнейших задач T. многообразий является задача классификации многообразий данной размерности п (напр., замкнутых) с точностью до диффеоморфности. При этом многие (хотя и не все - см. [3]) инварианты гладких многообразий оказываются топологич. и даже гомотопич. инвариантами. При п=1любое замкнутое многообразие есть окружность. При п =2любое замкнутое ориентированное многообразие есть поверхность нек-рого рода g>=0 а любое неориентированное-сфера с
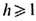 плёнками Мёбиуса. При n>=3 задача классификации не решена. Ряд топологич. инвариантов замкнутых ориентированных многообразий можно получить, интегрируя подходящие комбинации, компонент кривизны тензора Rijkl произвольной римановой метрики [обобщение ф-лы (2) для эйлеровой характеристики]. Так, напр., эйлерова характеристика 4-мерного многообразия вычисляется по ф-ле
плёнками Мёбиуса. При n>=3 задача классификации не решена. Ряд топологич. инвариантов замкнутых ориентированных многообразий можно получить, интегрируя подходящие комбинации, компонент кривизны тензора Rijkl произвольной римановой метрики [обобщение ф-лы (2) для эйлеровой характеристики]. Так, напр., эйлерова характеристика 4-мерного многообразия вычисляется по ф-ле
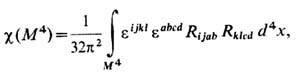
где eijkl -антисимметричный тензор 4-го ранга с e1234 = = 1,
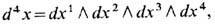 а 1-й к л а с с П о н т р я-г и н а-по ф-ле
а 1-й к л а с с П о н т р я-г и н а-по ф-ле

Для построения более сложных инвариантов 3-мерных и 4-мерных многообразий привлекают идеи и методы квантовой теории поля [4], [6].
Важна также задача гомотопич. классификации отображений многообразий (все отображения и гомотопии можно считать гладкими). Напр., задача отыскания топологич. характеристик (или топологических зарядов) n -компонентных полей
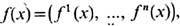 определённых на
определённых на  С заданной асимптотикой на бесконечности типа
С заданной асимптотикой на бесконечности типа 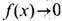 .при
.при 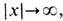 совпадает с задачей гомотопической классификации отображений сфер
совпадает с задачей гомотопической классификации отображений сфер 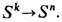 Полностью решается задача классификации отображений произвольного n -мерного замкнутого ориентированного многообразия Mn в n -мерную сферу Sn. Единственным инвариантом (или топологич. зарядом) отображения
Полностью решается задача классификации отображений произвольного n -мерного замкнутого ориентированного многообразия Mn в n -мерную сферу Sn. Единственным инвариантом (или топологич. зарядом) отображения 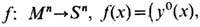
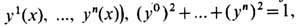 полностью определяющим его гомотопич. класс, является с т е п е н ь о т о бр а ж е н и я - целое число deg f вычисляемое по ф-ле
полностью определяющим его гомотопич. класс, является с т е п е н ь о т о бр а ж е н и я - целое число deg f вычисляемое по ф-ле
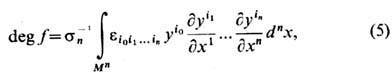
где sn -объём единичной n -мерной сферы. Укажем также и н в а р и а н т Х о п ф а-целое число, полностью определяющее гомотопич. класс отображений сфер
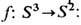
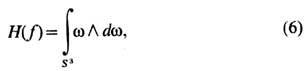
где 1-форма w на S3. такова, что
 , dS- форма площади на S2. (Интегральные ф-лы для топологич. зарядов отображений разл. многообразий и нек-рые их физ. приложения см. в [8 ].)
, dS- форма площади на S2. (Интегральные ф-лы для топологич. зарядов отображений разл. многообразий и нек-рые их физ. приложения см. в [8 ].)
Идеи и методы T. многообразий в ряде случаев удаётся применить к изучению функциональных пространств, рассматривая их как бесконечномерные многообразия. Важнейшими примерами являются п р о с т р а н с т в о п у т е й с фиксированными концами, расположенных на данном многообразии Mn, а также п р о с т р а н с т в о п е т е л ь (замкнутых кривых) на Mn.T. пространства путей и пространства петель на многообразии Mn оказывается тесно связанной с T. многообразия Mn. Это обстоятельство исключительно важно для решения задач вариационного исчисления в целом (см. ниже).
Ещё один важный класс топологич. пространств - к о м п л е к с ы, к-рые возникают как обобщения многогранников. T. комплексов является тем самым комбинаторной версией T. многообразий (хотя и находится с ней в тесных взаимоотношениях). Подобно тому как многообразия склеиваются из областей евклидова пространства, с и м п л и ц и а л ь н ы е к о м п л е к с ы склеиваются из с и м п л е к с о в - отрезков, треугольников и их многомерных обобщений, n -мерный симплекс определяется как выпуклая оболочка n+1 точек x0, x1,..., х n в n -мерном пространстве, не лежащих в одной n -мерной плоскости, т. е. совокупность точек вида

Г р а н и такого симплекса получаются приравниванием нулю части координат t0, t1, ..., tn. Симплициальным комплексом К наз. совокупность симплексов, удовлетворяющая след, двум требованиям: 1) вместе с каждым симплексом в комплексе содержатся все его грани; 2) любые два симплекса или не имеют общих точек, или пересекаются по целой грани. Напр., одномерный комплекс - это г р а ф. Комплекс К является топологич. пространством: открытыми являются те подмножества точек в К, пересечение к-рых с каждым симплексом открыто. Подразделением комплекса К наз. новый комплекс, получающийся из К разбиением каждой его грани на более мелкие части, превращающие саму эту грань в симплициальный комплекс. Числовые или алгебраич. характеристики топологич. свойств комплексов по определению должны совпадать для исходного и подразделённого комплексов, т. е. являться к о м б и н а т о р н ы м и и н в а р и а н т а м и. Большинство (но не все-см. [3]) комбинаторных инвариантов комплексов, напр. эйлерова характеристика
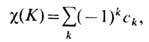
где ck - число k -мерных симплексов комплекса К, являются топологическими и даже гомотопическими инвариантами.
К у б и ч е с к и е к о м п л е к с ы определяются аналогично симплициальным, но вместо симплексов берутся кубы всех размерностей. Особый интерес такие комплексы вызывают потому, что евклидовы пространства допускают правильное разбиение на кубы (решётка). Связанные с кубич. комплексами топологич. задачи возникают поэтому при изучении моделей статистич. физики [9]. При вычислении нек-рых гомотопич. инвариантов пространств (напр., гомологии и гомотопических групп - см. ниже) используются также клеточные комплексы [3 ].
При изучении топологич. свойств методами а л г е бр а и ч е с к о й T. каждому (достаточно хорошему) пространству сопоставляется алгебраич. характеристика - линейное пространство, группа, кольцо и пр., причём это сопоставление (ф у н к т о р) должно обладать свойством е с т е с т в е н н о с т и или к о в а р и а н т н о с т и: отображениям топологич. пространств сопоставляются алгебраич. отображения (гомоморфизмы-см. Группа )их алгебраич. характеристик. Простейшим примером является ф у н д ам е н т а л ь н а я г р у п п а пространства. Элементами фундаментальной группы p1(X, x0 )пространства X с отмеченной точкой x0 являются гомотопические классы петель - замкнутых путей с началом и концом в точке x0 (в процессе гомотопии начало и конец пути должны оставаться в точке x0). Произведение путей определяется как их последовательное прохождение, а единичный элемент - постоянное отображение в точку x0. Эта группа, вообще говоря, некоммутативна. При изменении отмеченной точки x0 в связном пространстве X группа p1(X, x0) заменяется на изоморфную. Непрерывное отображение
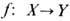 пространств X, Y с отмеченными точками
пространств X, Y с отмеченными точками 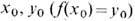 индуцирует гомоморфизм фундам. групп
индуцирует гомоморфизм фундам. групп 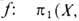
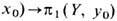 (ковариантность), не меняющийся при гомотопиях отображения f. Отсюда уже вытекает, что фундам. группа является гомотопическим инвариантом связного пространства. Поэтому для стягиваемого пространства- прямой, плоскости, евклидова пространства, дерева (графа без циклов) и др.- фундам. группа тривиальна, т. е. состоит только из единичного элемента. Пространства с тривиальной фундам. группой наз. о д н о с в я з н ы м и. Односвязной является также сфера, евклидово пространство с набором выколотых точек и др. Простейший пример неодносвязного пространства - окружность S1 (ей гомотопически эквивалентна плоскость с выколотой точкой):
(ковариантность), не меняющийся при гомотопиях отображения f. Отсюда уже вытекает, что фундам. группа является гомотопическим инвариантом связного пространства. Поэтому для стягиваемого пространства- прямой, плоскости, евклидова пространства, дерева (графа без циклов) и др.- фундам. группа тривиальна, т. е. состоит только из единичного элемента. Пространства с тривиальной фундам. группой наз. о д н о с в я з н ы м и. Односвязной является также сфера, евклидово пространство с набором выколотых точек и др. Простейший пример неодносвязного пространства - окружность S1 (ей гомотопически эквивалентна плоскость с выколотой точкой): 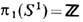 (группа целых чисел). [Если задать петлю на S1 функцией f(t), удовлетворяющей условию
(группа целых чисел). [Если задать петлю на S1 функцией f(t), удовлетворяющей условию 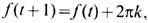 то целое число k и будет единственным топологич. зарядом этой петли] Примерами пространств с неабелевой фундам. группой являются плоскость с n>=2 выколотыми точками, а также поверхности рода g>=2. Для проективных пространств группа
то целое число k и будет единственным топологич. зарядом этой петли] Примерами пространств с неабелевой фундам. группой являются плоскость с n>=2 выколотыми точками, а также поверхности рода g>=2. Для проективных пространств группа 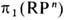 состоит из двух элементов +1, - 1. [Если задать петлю на RPn не обращающейся в нуль вектор-функцией (u0(t), u1(t), ...,un(t)), причём
состоит из двух элементов +1, - 1. [Если задать петлю на RPn не обращающейся в нуль вектор-функцией (u0(t), u1(t), ...,un(t)), причём 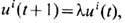 i= 0, 1,..., n, то соответствующий элемент + 1 фундам. группы совпадает со знаком l. ]
i= 0, 1,..., n, то соответствующий элемент + 1 фундам. группы совпадает со знаком l. ]
Аналогично определяются высшие гомотопич. группы pk (X, x0). Их элементами являются гомотопич. классы отображений k -мерной сферы (с отмеченной точкой) в X. Эти группы при k>=2 абелевы. Особенно важны гомотопич. группы сфер
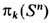 , нетривиальные при k>=n.. Известно, напр., что
, нетривиальные при k>=n.. Известно, напр., что 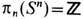 [топологич. заряд - степень отображения (5)],
[топологич. заряд - степень отображения (5)], 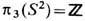 [топологич. заряд - инвариант Хопфа (6)]. До настоящего времени при всех k, n группы
[топологич. заряд - инвариант Хопфа (6)]. До настоящего времени при всех k, n группы 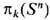 не вычислены. (Таблицу известных гомотопич. групп сфер см. в [2].)
не вычислены. (Таблицу известных гомотопич. групп сфер см. в [2].)
Более простыми топологическими (и гомотопическими) характеристиками являются г о м о л о г и и и к о г о м о л о г и и пространств. Проще всего определить когомологии многообразий. Элементами k- йгруппы (и даже линейного пространства) когомологий
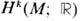 являются классы эквивалентности замкнутых дифференц. k -форм,
являются классы эквивалентности замкнутых дифференц. k -форм,
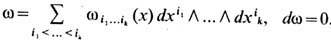 , на многообразии M, рассматриваемых с точностью до т о ч н ы х ф о р м: w~w' ,если w-w'=ds ,где s-(k-1)-форма. Размерность пространства
, на многообразии M, рассматриваемых с точностью до т о ч н ы х ф о р м: w~w' ,если w-w'=ds ,где s-(k-1)-форма. Размерность пространства 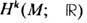 наз. k- мч и с л о м Б е т т и
наз. k- мч и с л о м Б е т т и 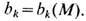 Известно, что b0 равно числу связных компонент M, сумма b0 - b1+b2 - ... равна эйлеровой характеристике M. Если многообразие Mn n -мерно, то
Известно, что b0 равно числу связных компонент M, сумма b0 - b1+b2 - ... равна эйлеровой характеристике M. Если многообразие Mn n -мерно, то 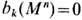 при k>n;для замкнутых ориентируемых многообразий имеет место д в о й с т в е н н о с т ь П у а н к а р е:
при k>n;для замкнутых ориентируемых многообразий имеет место д в о й с т в е н н о с т ь П у а н к а р е: 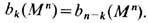 Напр., для n -мерной сферы b0 = bn =1, остальные числа Бетти нулевые. Для стягиваемых M в силу гомотопич. инвариантности когомологии тривиальны: bk =0 при k>0. Тем самым, в частности, из замкнутости dw=0 формы w вытекает существование локальной формы s , такой, что w=ds (утверждение, обобщающее условия потенциальности или соленоидальности векторных полей).
Напр., для n -мерной сферы b0 = bn =1, остальные числа Бетти нулевые. Для стягиваемых M в силу гомотопич. инвариантности когомологии тривиальны: bk =0 при k>0. Тем самым, в частности, из замкнутости dw=0 формы w вытекает существование локальной формы s , такой, что w=ds (утверждение, обобщающее условия потенциальности или соленоидальности векторных полей).
Элементами k -мерной группы гомологии
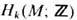 пространства M, говоря наглядно, являются k- мерные циклы (или, иначе, ориентированные замкнутые k- мерные плёнки) в M и их формальные линейные комбинации с целыми коэффициентами. При этом два цикла считаются эквивалентными (г о м о л о г и ч н ы м и), если они служат границей (k+1)-мерной плёнки (рис. 6, для k=1). Для строгого определения групп гомологии приходится заменять пространство M на гомотопически эквивалентный ему комплекс [3]. Примеры: для поверхностей M2 рода g имеем:
пространства M, говоря наглядно, являются k- мерные циклы (или, иначе, ориентированные замкнутые k- мерные плёнки) в M и их формальные линейные комбинации с целыми коэффициентами. При этом два цикла считаются эквивалентными (г о м о л о г и ч н ы м и), если они служат границей (k+1)-мерной плёнки (рис. 6, для k=1). Для строгого определения групп гомологии приходится заменять пространство M на гомотопически эквивалентный ему комплекс [3]. Примеры: для поверхностей M2 рода g имеем:
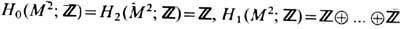 (2gcлагаемых); для проективной плоскости
(2gcлагаемых); для проективной плоскости 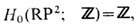
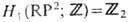 (группа из двух элементов),
(группа из двух элементов),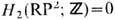 Если в определении гомологии брать линейные комбинации циклов с любыми вещественными коэф., то получаются группы (линейные пространства)
Если в определении гомологии брать линейные комбинации циклов с любыми вещественными коэф., то получаются группы (линейные пространства) 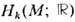 (в качестве коэф. иногда полезно также брать элементы из любой абелевой группы). Ф-ла
(в качестве коэф. иногда полезно также брать элементы из любой абелевой группы). Ф-ла  где w-замкнутая k- форма, а g- k -мерный цикл, определяет [в силу ф-лы Стокса (4)] невырожденное скалярное произведение между пространствами
где w-замкнутая k- форма, а g- k -мерный цикл, определяет [в силу ф-лы Стокса (4)] невырожденное скалярное произведение между пространствами 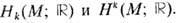 Поэтому эти пространства гомологии и когомологий имеют одинаковую размерность [равную числу Бетти bk(M)].
Поэтому эти пространства гомологии и когомологий имеют одинаковую размерность [равную числу Бетти bk(M)].
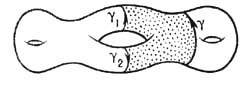
Рис. 6. Гомологичные циклы g и g'=g1-g2 (двумерная плёнка между ними заштрихована).
Более сложные гомотопич. характеристики пространств, возникающие в алгебраич. Т.,- экстраординарные гомологии (напр., бордизмы, K -теория и др. [3]).
Важной сферой применения теории гомологии является вариационное исчисление в целом (этот раздел T. называют т е о р и е й М о р с а). Удаётся выводить существование решений вариационных задач на многообразии из информации о его гомологиях. Обобщение теории Морса на многозначные функционалы найдено в [10] (см. также [3]).
T. р а с с л о е н и й играет важную вспомогат. роль во многих топологич. вычислениях: её задачи имеют также и самостоятельную (в т. ч. прикладную) ценность. Интуитивно, расслоение с базой В и слоем F есть семейство одинаковых слоев Fx, непрерывно зависящих от точки x базы В (F, В- нек-рые пространства, напр. многообразия); объединение E всех слоев Fx наз. п р о с т р а нс т в о м р а с с л о е н и я, а отображение
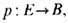 переводящее каждую точку слоя Fx в х,- п р о е к ц и е й р а с с л о ен и я. Простейшим примером служит прямое произведение E=F х В, где Fx состоит из пар вида (f, x),f- точка из F. Более сложный пример - лист Мёбиуса (расслоение с базой окружность и слоем отрезок). Если слой F является дискретным множеством, то расслоение наз. н а к р ы т ие м. Напр., отображение
переводящее каждую точку слоя Fx в х,- п р о е к ц и е й р а с с л о ен и я. Простейшим примером служит прямое произведение E=F х В, где Fx состоит из пар вида (f, x),f- точка из F. Более сложный пример - лист Мёбиуса (расслоение с базой окружность и слоем отрезок). Если слой F является дискретным множеством, то расслоение наз. н а к р ы т ие м. Напр., отображение 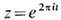 задаёт накрытие прямой над окружностью |z|=1, слоем является совокупность целых чисел. Накрытия - осн. инструмент при вычислении фундам. групп. Более сложные расслоения используются для вычисления гомотопич. групп. Для вычисления гомологии и когомологий расслоений используется техника спектральных последовательностей [3], [11].
задаёт накрытие прямой над окружностью |z|=1, слоем является совокупность целых чисел. Накрытия - осн. инструмент при вычислении фундам. групп. Более сложные расслоения используются для вычисления гомотопич. групп. Для вычисления гомологии и когомологий расслоений используется техника спектральных последовательностей [3], [11].
Осн. задачей T. расслоений является задача классификации расслоений. По определению, гомоморфизм
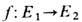 задаёт э к в и в а л е н т н о с т ь двух расслоений
задаёт э к в и в а л е н т н о с т ь двух расслоений  и р2:
и р2: 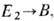 если он сохраняет слои, т. е.
если он сохраняет слои, т. е. 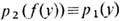 для всех у из E1. Расслоение, эквивалентное прямому произведению, наз. т р и в и а л ь н ы м. Расслоения над евклидовым пространством (без ограничений на поведение в бесконечности) тривиальны; G -расслоения над n -мерной сферой Sn классифицируются элементами гомотопич. группы
для всех у из E1. Расслоение, эквивалентное прямому произведению, наз. т р и в и а л ь н ы м. Расслоения над евклидовым пространством (без ограничений на поведение в бесконечности) тривиальны; G -расслоения над n -мерной сферой Sn классифицируются элементами гомотопич. группы 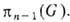 Топологич. характеристики расслоений наз. х а р а к т е р и с т и ч е с к и м и к л а с с а м и. Для расслоений со структурной группой G (где G - группа Ли) харак-теристич. классы могут быть выражены через кривизну расслоения, определяя тем самым топологич. заряды связ ностей в расслоении (или, эквивалентно, калибровочных полей). Напр., единств. топологич. инвариантом, задающим U(1)-расслоение над двумерной сферой S2, является п е р в ы й к л а с с Ч е р н а (Ч ж э н я)
Топологич. характеристики расслоений наз. х а р а к т е р и с т и ч е с к и м и к л а с с а м и. Для расслоений со структурной группой G (где G - группа Ли) харак-теристич. классы могут быть выражены через кривизну расслоения, определяя тем самым топологич. заряды связ ностей в расслоении (или, эквивалентно, калибровочных полей). Напр., единств. топологич. инвариантом, задающим U(1)-расслоение над двумерной сферой S2, является п е р в ы й к л а с с Ч е р н а (Ч ж э н я)
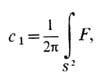
где
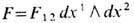 -форма кривизны расслоения;
-форма кривизны расслоения; 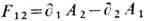 , а для SU(2)-расслоений над 4-мерной сферой S4 - в т о р о й к л а с с Ч ж э н я
, а для SU(2)-расслоений над 4-мерной сферой S4 - в т о р о й к л а с с Ч ж э н я

где
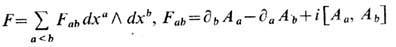
- матричная форма кривизны расслоения (интегралы нормированы условием целочисленности величин c1 и c2).
Осн. топологич. характеристикой эллиптич. оператора является его и н д е к с. (Это понятие возникло при исследовании краевых задач теории упругости.) Индексом линейного оператора
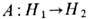 [где H1, H2 -гильбертовы пространства, оператор А должен быть нетеровым, т. е. должен иметь конечномерное ядро-совокупность решений ур-ния Ay=0, и коядро-совокупность решений сопряжённого ур-ния
[где H1, H2 -гильбертовы пространства, оператор А должен быть нетеровым, т. е. должен иметь конечномерное ядро-совокупность решений ур-ния Ay=0, и коядро-совокупность решений сопряжённого ур-ния  (здесь
(здесь 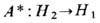 - сопряжённый оператор)] называется разность размерностей ядра и коядра. Индекс является гомотопич. инвариантом оператора, не меняясь при деформации А в классе нетеровых операторов. Для эллиптич. оператора на многообразии (условие нетеровости выполнено) теорема об индексе позволяет вычислить индекс оператора через топологич. характеристики многообразия [4]. Это позволяет, в частности, в ряде случаев вычислять размерность пространства решений ур-ния вида Ay=0(т. е. число нулевых мод оператора А).
- сопряжённый оператор)] называется разность размерностей ядра и коядра. Индекс является гомотопич. инвариантом оператора, не меняясь при деформации А в классе нетеровых операторов. Для эллиптич. оператора на многообразии (условие нетеровости выполнено) теорема об индексе позволяет вычислить индекс оператора через топологич. характеристики многообразия [4]. Это позволяет, в частности, в ряде случаев вычислять размерность пространства решений ур-ния вида Ay=0(т. е. число нулевых мод оператора А).
Топологич. методы оказываются также весьма полезными в ряде задач качественной теории динамич. систем и слоений: в задачах топологич. классификации таких систем, описания их инвариантных и предельных множеств и др.
Лит.:1) Фукс Д. Б., Классические многообразия, в кн.: Итоги науки и техники. Современные проблемы математики. Фундаментальные направления, т. 12, M., 1985, с. 253; 2) Дубровин Б. А., Новикове. П., Фоменко А. Т., Современная геометрия. Методы и приложения, 2 изд., M., 1986; 3) их же, Современная геометрия. Методы теории гомологии, M., 1984; 4) Шварц А. С., Квантовая теория поля и топология, M., 1989; 5) Гуревич В., Вол-мэн Г., Теория размерности, пер. с англ., M., 1948; 6) Witten E., Some geometrical applications of quantum field theory, in: IX International Congress on Mathematical Physics, Bristol-N. Y., 1989, p. 77; 7) Бессе А., Многообразия Эйнштейна, пер. с англ., т. 1-2, M., 1990; 8) Новиков С. П., Аналитический обобщенный инвариант Хопфа. Многозначные функционалы, "Успехи матем. наук", 1984, т. 39, № 5, с. 97; 9) Долбилин H. П., Штанько M. А., Штогрин M. И., Комбинаторные вопросы двумерной модели Изинга, "Труды МИАН", 1991, т. 196, с. 51; 10) Новиков С. П., Гамильтонов формализм и многозначный аналог теории Морса, "Успехи матем. наук", 1982, т. 37, № 5, с. 3; И) Фоменко А. Т., Фукс Д. Б., Курс гомотопической топологии, M., 1989.
Б. А. Дубровин.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
