- Непустое множество
-
Пустым множеством в математике называется множество, не содержащее ни одного элемента.
В одних теориях множеств существование [по меньшей мере одного] пустого множества провозглашается (см. аксиому пустого множества), в других — доказывается. Во всех теориях множеств единственность пустого множества доказывается (см. аксиому объёмности).
Содержание
Обозначения пустого множества
 Обозначение пустого множества
Обозначение пустого множестваОбычно пустое множество обозначают одним из следующих символов:
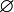 ,
, 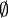 и
и 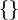 .
.Реже пустое множество обозначают одним из следующих символов:
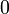 и
и 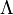
В Юникоде имеется специальный символ "пустое множество" (U+2205,∅).
Символы
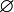 и
и 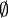 введены в употребление группой Бурбаки (в частности, Андре Вейлем) в 1939 году.
введены в употребление группой Бурбаки (в частности, Андре Вейлем) в 1939 году.Символ
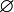 идентичен букве Ø в Датско-норвежском алфавите.[1]
идентичен букве Ø в Датско-норвежском алфавите.[1]Свойства пустого множества
- Ни одно множество не является элементом пустого множества. Иначе говоря,
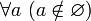 и, в частности,
и, в частности, 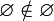 .
. - Пустое множество является подмножеством любого множества. Иначе говоря,
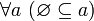 и, в частности,
и, в частности, 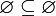 .
. - Объединение пустого множества с любым множеством равно последнему [указанному множеству]. Иначе говоря,
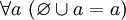 и, в частности,
и, в частности, 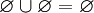 .
. - Пересечение пустого множества с любым множеством равно пустому множеству. Иначе говоря,
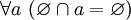 и, в частности,
и, в частности, 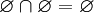 .
. - Исключение пустого множества из любого множества равно последнему [указанному множеству]. Иначе говоря,
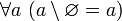 и, в частности,
и, в частности, 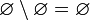 .
. - Исключение любого множества из пустого множества равно пустому множеству. Иначе говоря,
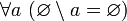 и, в частности,
и, в частности, 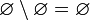 .
. - Симметрическая разность пустого множества с любым множеством равна последнему [указанному множеству]. Иначе говоря,
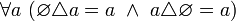 и, в частности,
и, в частности, 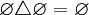
- Декартово произведение пустого множества на любое множество равно пустому множеству. Иначе говоря,
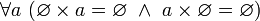 и, в частности,
и, в частности, 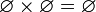 .
. - Пустое множество — транзитивно. Иначе говоря,
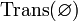 , где
, где 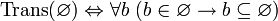 .
. - Пустое множество — ординал. Иначе говоря,
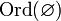 , где
, где 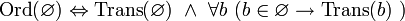 .
. - Мощность пустого множества равна нулю. Иначе говоря,
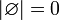 .
. - Мера пустого множества равна нулю. Иначе говоря,
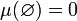
См. также
Ссылки
- Ни одно множество не является элементом пустого множества. Иначе говоря,
Wikimedia Foundation. 2010.
