ВПОЛНЕ УПОРЯДОЧЕННОЕ МНОЖЕСТВО

ВПОЛНЕ УПОРЯДОЧЕННОЕ МНОЖЕСТВО

множество Рс заданным на нем бинарньш отношением , удовлетворяющим условиям:


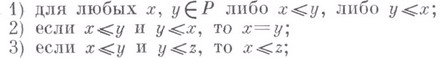
4) в любом непустом подмножестве ~ существует такой элемент а, что для всех ; таким образом В. у. м.- линейно упорядоченное множество, удовлетворяющее условию минимальности.

Понятие В. у. м. было введено Г. Кантором [1]. Примером В. у. м. служит естественным образом упорядоченное множество натуральных чисел. С другой стороны, отрезок действительных чисел [0, 1] с естественным порядком не является В. у. м. Любое подмножество В. у. м. само вполне упорядоченное. Декартово произведение конечного числа В. у. м. вполне упорядочено отношением лексикографического порядка. Линейно упорядоченное множество является вполне упорядоченным тогда и только тогда, когда оно не содержит подмножества, антиизоморфного (см. Антиизоморфизм частично -упорядоченных множеств) множеству натуральных чисел.

Наименьший элемент В. у. м. Рназ. нулем (и обозначается 0). Для любого элемента множество наз. начальным отрезком множества Р. Для всякого элемента а, не являющегося наибольшим в Р, существует элемент, непосредственно следующий за ним; его принято обозначать a+1. Элемент В. у. м., не имеющий непосредственно предшествующего, называется предельным.

Теорема о сравнении. Для любых двух В. у. м. P1 и P2 имеет место одна и только одна из следующих ситуаций: 1) Р 1 изоморфно Р 2 ,2) Р 1 изоморфно некоторому начальному отрезку множества Р 2 ,3) Р 2 изоморфно начальному отрезку множества P1.

Принимая в числе аксиом теории множеств выбора аксиому, можно доказать, что на всяком непустом множестве можно ввести отношение порядка, превращающее его во В. у. м. (т. е. всякое непустое множество можно вполне упорядочить). Эта теорема, называемая теоремой Цермело, на самом деле эквивалентна аксиоме выбора. Теорема Цермело и теорема о сравнении служат основанием для сравнения множеств по их мощности. Порядковые типы В. у. м. наз. трансфинитами, или трансфинитными числами.

Лит.:[1] Cantor G., "Math. Ann.", 1883, Bd 21, S. 51-8; [2] Александров П. С., Введение в общую теорию множеств и функций, М.-Л., 1948; [3] ХаусдорфФ., Теория множеств, пер. с нем., М.-Л., 1937; [4] Бурбаки Н., Теория множеств, пер. с франц., М., 1965; [5] Куратовский К., Мостовский А., Теория множеств, пер с англ., М., 1970. Б. А. Ефимов, Т. С. Фофанова.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужно сделать НИР?

Полезное


Смотреть что такое "ВПОЛНЕ УПОРЯДОЧЕННОЕ МНОЖЕСТВО" в других словарях:

  • Вполне упорядоченное множество — У этого термина существуют и другие значения, см. Упорядоченное множество. Вполне упорядоченное множество  линейно упорядоченное множество M такое, что в любом его непустом подмножестве есть минимальный элемент, другими словами это… …   Википедия

  • Упорядоченное множество — Упорядоченное множество  множество с заданным отношением порядка. Частично упорядоченное множество Линейно упорядоченное множество Вполне упорядоченное множество …   Википедия

  • Частично упорядоченное множество — У этого термина существуют и другие значения, см. Упорядоченное множество. Подмножества {x, y, z}, упо …   Википедия

  • Линейно упорядоченное множество — У этого термина существуют и другие значения, см. Упорядоченное множество. Линейно упорядоченное множество или цепь ― частично упорядоченное множество, в котором для любых двух элементов и имеет место или . Важнейший частный случай линейно… …   Википедия

  • ЛИНЕЙНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО, — цепь, частично упорядоченное множество, в к ром для любых двух элементов аи bимеет место или Подмножество Л. у. м. само является Л. у. м. Всякий максимальный (минимальный) элемент Л. у. м. оказывается наибольшим (наименьшим). Важнейший частный… …   Математическая энциклопедия

  • Множество (математика) — Множество  один из ключевых объектов математики, в частности, теории множеств. «Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» (Г. Кантор). Это не является в полном… …   Википедия

  • Упорядоченное — Упорядоченное  фантастическая вселенная из произведений Ника Перумова. Представляет собой многомерную гипервселенную, состоящую из нескольких миллиардов миров, аналогичную Planescape. Из большинства миров можно попасть в другие, с помощью… …   Википедия

  • Направленное множество — В математике, направленным множеством называется непустое множество A с заданным на нем рефлексивным транзитивным отношением ≤ (т. е. предпорядком), обладающее дополнительным свойством: для любых двух элементов из A найдется элемент из A… …   Википедия

  • Ограниченное множество — В математическом анализе, и прилегающих разделах математики, ограниченное множество  множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай… …   Википедия

  • Ограниченное числовое множество — В математическом анализе, и прилегающих разделах математики, ограниченное множество  множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай… …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»