НИГДЕ НЕ ПЛОТНОЕ МНОЖЕСТВО
- НИГДЕ НЕ ПЛОТНОЕ МНОЖЕСТВО
топологического пространства X- множество А, определяемое следующим свойством: каждое непустое открытое множество  содержит непустое открытое множество
содержит непустое открытое множество  такое, что
такое, что 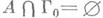 . Другими словами, А- Н. не п. м., если оно не плотно ни в каком непустом открытом множестве.
. Другими словами, А- Н. не п. м., если оно не плотно ни в каком непустом открытом множестве.
М. И. Войцеховский.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "НИГДЕ НЕ ПЛОТНОЕ МНОЖЕСТВО" в других словарях:
Нигде не плотное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Плотное множество — подмножество пространства, точками которого можно сколь угодно хорошо приблизить любую точку объемлющего пространства. Формально говоря, A плотно в X, если всякая окрестность любой точки x из X содержит элемент A. Содержание 1 Определения 2… … Википедия
ПЛОТНОЕ МНОЖЕСТВО — то же, что всюду плотное множество. Более общо, множество Аназ. плотным в открытом множестве Gпространства X, если G содержится в замыкании Аили, что то же самое, если всюду плотно в подпространстве . Если Ане плотно ни в каком непустом открытом… … Математическая энциклопедия
Всюду плотное множество — Плотное множество подмножество, точками которого можно приблизить любую точку объемлющего пространства. Содержание 1 Определения 2 Замечание 3 Примеры 4 См. также … Википедия
Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Массивное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Несвязное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Связное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
АНАЛИТИЧЕСКОЕ МНОЖЕСТВО — подмножество полного сепарабельного метрич. пространства, являющееся непрерывным образом пространства иррациональных чисел. Понятие А. м. введено Н. Н. Лузиным [1]. Это классич. определение А. м. обобщается на случай общих метрич. и топологич.… … Математическая энциклопедия
 содержит непустое открытое множество
содержит непустое открытое множество  такое, что
такое, что 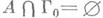 . Другими словами, А- Н. не п. м., если оно не плотно ни в каком непустом открытом множестве.
. Другими словами, А- Н. не п. м., если оно не плотно ни в каком непустом открытом множестве. 