- УНИВЕРСАЛЬНАЯ ОБЕРТЫВАЮЩАЯ АЛГЕБРА
алгебры Ли
 над коммутативным кольцом kс единицей - ассоциативная k- алгебра
над коммутативным кольцом kс единицей - ассоциативная k- алгебра  с единицей, снабженная отображением
с единицей, снабженная отображением  для к-рой выполнены следующие свойства: 1) о является гомоморфизмом алгебр Ли, т. е.
для к-рой выполнены следующие свойства: 1) о является гомоморфизмом алгебр Ли, т. е. Ус-линейно и
Ус-линейно и  2) для любой ассоциативной k-алгебры Ас единицей и всякого такого k-линейного отображения
2) для любой ассоциативной k-алгебры Ас единицей и всякого такого k-линейного отображения  что
что  существует единственный гомоморфизм ассоциативных алгебр
существует единственный гомоморфизм ассоциативных алгебр 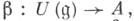 переводящий единицу в единицу, для к-рого
переводящий единицу в единицу, для к-рого  У. о. а. определяется однозначно с точностью до изоморфизма и всегда существует: если
У. о. а. определяется однозначно с точностью до изоморфизма и всегда существует: если 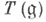 - тензорная алгебра k-модуля
- тензорная алгебра k-модуля  I - ее двусторонний идеал, порожденный элементами вида [ х, у] -
I - ее двусторонний идеал, порожденный элементами вида [ х, у] -  и
и  - каноническое отображение, то
- каноническое отображение, то  - У. о. а. для
- У. о. а. для 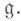
Если kнётерово, а модуль конечного порядка, то алгебра
конечного порядка, то алгебра 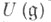 - нётерова слева и справа. Если
- нётерова слева и справа. Если  - свободный модуль над областью целостности k, то
- свободный модуль над областью целостности k, то 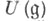 не имеет делителей нуля. Для любой конечномерной алгебры Ли
не имеет делителей нуля. Для любой конечномерной алгебры Ли  над полем kалгебра
над полем kалгебра  удовлетворяет условию Оре (см. Вложение полугруппы )и тем самым обладает телом частных.
удовлетворяет условию Оре (см. Вложение полугруппы )и тем самым обладает телом частных.
Если V - нек-рый k-модуль, то всякий гомоморфизм алгебр продолжается до гомоморфизма ассоциативных алгебр
продолжается до гомоморфизма ассоциативных алгебр  Этим устанавливается изоморфизм категории
Этим устанавливается изоморфизм категории  -модулой и категории левых
-модулой и категории левых  -модулей, существование к-рого лежит в основе применений У. о. а. в теории представлений алгебр Ли (см. [3], [4]).
-модулей, существование к-рого лежит в основе применений У. о. а. в теории представлений алгебр Ли (см. [3], [4]).
У. о. а. прямого произведения алгебр Ли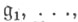
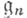 есть тензорное произведение алгебр
есть тензорное произведение алгебр 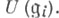 Если
Если  - подалгебра в
- подалгебра в  причем
причем  и
и  - свободные k-модули, то канонический гомоморфизм
- свободные k-модули, то канонический гомоморфизм  является вложением. Если k' - расширение поля k, то
является вложением. Если k' - расширение поля k, то 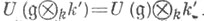 У. о. а. обладает канонической фильтрацией
У. о. а. обладает канонической фильтрацией  где
где  а
а 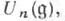 n>0,- k-подмодуль в
n>0,- k-подмодуль в  порожденный произведениями
порожденный произведениями 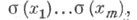
 для всех i. Ассоциированная с этой фильтрацией градуированная алгебра
для всех i. Ассоциированная с этой фильтрацией градуированная алгебра  коммутативна и порождается образом естественного отображения
коммутативна и порождается образом естественного отображения  это отображение определяет гомоморфизм
это отображение определяет гомоморфизм 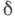 симметрической алгебры
симметрической алгебры  k-модуля
k-модуля  в
в  Согласно теореме Пуанкаре- Биркгофа - Витта
Согласно теореме Пуанкаре- Биркгофа - Витта  - изоморфизм алгебр, если
- изоморфизм алгебр, если 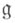 - свободный k-модуль. Эквивалентная формулировка состоит в следующем: если
- свободный k-модуль. Эквивалентная формулировка состоит в следующем: если  - базис k-модуля
- базис k-модуля 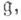 где I - линейно упорядоченное множество, то семейство одночленов
где I - линейно упорядоченное множество, то семейство одночленов 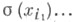
 образует базис k-модуля
образует базис k-модуля 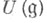 (в частности,
(в частности,  инъективно).
инъективно).
Пусть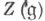 - центр алгебры
- центр алгебры  Тогда для любой конечномерной алгебры Ли
Тогда для любой конечномерной алгебры Ли 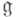 над полем характеристики 0
над полем характеристики 0  совпадает с подалгеброй G-инвариантных элементов в
совпадает с подалгеброй G-инвариантных элементов в  Если
Если  полупроста, то
полупроста, то  является алгеброй многочленов от
является алгеброй многочленов от  переменных.
переменных.
Одним из важнейших направлений исследования У. о. а. является изучение их примитивных идеалов (см. [3]).Лит.:[1] Бурбаки Н., Группы и алгебры Ли. Алгебры Ли, свободные алгебры Ли и группы Ли, пер. с франц., М., 1976; [2] его же, Группы и алгебры Ли. Подалгебры Картана, регулярные элементы, расщепляемые полупростые алгебры Ли, пер. с франц., М., 1978; [3] Диксмье Ж., Универсальные обертывающие алгебры, пер. с франц., М., 1978; [4] Кириллов А. А., Элементы теории представлений, 2 изд., М., 1978; [5] Гельфанд И. М., лМатем. сб.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
