ЛИ ГРАДУИРОВАННАЯ АЛГЕБРА

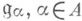алгебра Ли над полем К, градуированная при помощи нек-рой абелевой группы А, т. е. разложенная в прямую сумму подпространств , таким образом, что Если А - упорядоченная группа, то для каждой фильтрованной алгебры Ли ассоциированная с ней градуированная алгебра является Ли г. а.

Ли г. а. играют важную роль в классификации простых конечномерных алгебр Ли, йордановых алгебр и их обобщений, примитивных псевдогрупп преобразований (см. [3], [4]). Для любой полупростой вещественной алгебры Ли ее Картана разложение может рассматриваться как -градуировка. Локальная классификация римановых симметрич. пространств сводится к классификации -градуированных простых комплексных алгебр Ли [6].

Некоторые конструкции градуированных алгебр Ли. 1) Пусть U- ассоциативная алгебра, снабженная возрастающей фильтрацией причем где d - фиксированное натуральное число, и Тогда операция коммутирования в U индуцирует в пространстве структуру -градуированной алгебры Ли. Таким путем могут быть получены нек-рые алгебры Ли функций с Пуассона скобкой ъ качество коммутатора. В следующих двух примерах при k>0 и U_k=0 при k<0. а) Пусть U - алгебра линейных дифференциальных операторов с полиномиальными коэффициентами, U₁- подпространство, натянутое на се образующие i=l, . . ., т. Тогда и U есть алгебра Ли многочленов от р _i, g_i с обычной скобкой Пуассона. б) Пусть U - универсальная обертывающая алгебра конечномерной алгебры Ли причем U₁=g. Тогда и канонически изоморфна (как векторное пространство) симметрич. алгебре над т. е. алгебре многочленов на сопряженном пространстве (теорема Пуанкаре - Бнркгофа-Витта). Если - алгебра Ли связной группы Ли G, то коммутатор элементов из можно интерпретировать либо как скобку Пуассона для соответствующих левоинвариантных функций на кокасательном расслоении T*G, либо как скобку Пуассона на каждой орбите ко-присоединенного представления, определяемую посредством стандартной симплектич. структуры на этих орбитах.

2) Пусть char Eесть re-мерное векторное пространство над К, снабженное невырожденной квадратичной формой Q', e₁, ..., е _п - нек-рый ортогональный базис в Е. Разложение Клиффорда алгебры С(Q).в сумму одномерных подпространств i₁, ..., i_k, является ее -градуировкой. При n=2m элементы алгебры С(Q).с нулевым следом образуют простую Ли г. а. типа ее градуировка обладает высокой степенью симметрии; в частности, все градуирующие подпространства равноправны. Аналогичные градуировки (при помощи различных конечных групп) имеются и у других простых алгебр Ли [1].

3) Каждой псевдогруппе Ли преобразований отвечает нек-рая алгебра Ли векторных полей. Росток lэтой алгебры Ли в любой точке обладает естественной

-фильтрацией

где к l_k относятся ростки тех векторных полой, координаты к-рых разлагаются в степенные ряды без членов степени меньше чем k+l. Ассоциированная Ли г. а. может быть интерпретирована как нек-рая алгебра Ли полиномиальных векторных полей.

Классификация простых градуированных алгебр Ли. Простым примитивным псевдогруппам Ли соответствуют следующие 4 серии простых бесконечномерных Ли г. а. (см. [5]):

W_n- алгебра Ли всех полиномиальных векторных полей в n-мерном аффинном пространстве;

S_n - ее подалгебра, состоящая из векторных полей с нулевой дивергенцией;

Н _п, где n=2m,- подалгебра, состоящая из векторных полей, аннулирующих дифференциальную форму

(гамильтоновых векторных полей);

К _n, где n=2m+l,- подалгебра, состоящая из векторных полей, умножающих дифференциальную форму

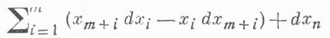
на функцию.

Над полями характеристики р>0 могут быть определены простые конечномерные Ли г. а., аналогичные W_n, S_n, Н _n и K_n (см. [5]).

Простые Ли г. а. другого типа получаются следующим образом [4]. Пусть - алгебра Ли, определяемая при помощи неразложимой матрицы Картана 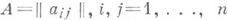(здесь и далее употребляются обозначения статьи Картана матрица). Алгебра снабжается -градуировкой так, что

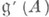- строка (0. . .1. . .0), причем 1 стоит на i-м месте. Элементы для к-рых наз. корнями, а a_i - простыми корнями. Всякий корень есть линейная комбинация простых корней с целыми коэффициентами одного знака и для любого Факторалгебра алгебры по ее центру, лежащему в 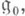проста как градуированная алгебра, т. е. не имеет нетривиальных градуирован, идеалов.

Пусть Р- совокупность линейных комбинаций строк матрицы Ас положительными коэффициентами. Имеет место один из следующих случаев:

(П) Рсодержит строку, все элементы к-рой положительны;

(Н) Рсодержит нулевую строку;

(О) Рсодержит строку, все элементы к-рой отрицательны.

В случае - простая конечномерная алгебра Ли. В случае - простая бесконечномерная алгебра Ли. В случае (Н) алгебра проста лишь как градуированная алгебра. Она может быть превращена в -алгебру так, что: а) где v - нек-рая строка из положительных чисел; б) факторалгебра есть простая конечномерная алгебра Ли. Наибольший общий делитель всех компонент v_i строки v, равный 1, 2 или 3, наз. индексом алгебры

В следующей таблице приведен список всех простых Ли г. а. с матрицей Картана типа (Н). Здесь алгебра 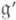обозначается так же, как и но с добавлением ее индекса, указываемого в скобках.

Схема простых корней описывает матрицу А. Ее вершины соответствуют простым корням; i-я и j-я вершины соединены (а _ij а _jy )-кратным ребром, ориентированным от i-й вершины к j-й, если и неориентированным, если Возле вершин указаны числа v_i.

С помощью Ли г. а. с матрицей Картана типа (Н) классифицируются -градуированные простые конечномерные алгебры Ли (см. [4], [2]). А именно, пусть где Аудовлетворяет условию (Н), и - такей гомоморфизм, что

Тогда при любом изоморфно отображается на подпространство зависящее только от вычета kпо модулю т, и разложение есть -градуировка алгебры Если поле Калгебраически замкнуто, то описанным способом получаются, причем без повторений, все градуированные простые конечномерные алгебры Ли над К. Индекс алгебры равен порядку автоморфизма алгебры по модулю группы внутренних автоморфизмов.

Имеется классификация простых -градуированных алгебр Ли удовлетворяющих условиям: а) для нек-рых Си N;б) порождается подпространством в) представление на неприводимо. В этом случае либо конечномерна, либо есть одна из алгебр W_n, S_n, Н _п, К _п, либо есть алгебра определяемая матрицей Картана типа (Н), снабженная подходящей -градуировкой [4].

Иногда -градуированной алгеброй Ли наз. супералгебра Ли.

Лит.:[1] Алексеевский А. В., "Функциональный анализ и его приложения", 1974, т. 8, № 4, с. 1-4; [2] В и н б е р г Э. Б. "Изв. АН СССР. Сер. матем.", 1976, т. 40, № 3, с. 488-526; [3] К а н т о р И. Л., "Тр. семинара по векторному и тензорному анализу...", 1972, в. 16, с. 407-99; [4] К а ц В. Г., "Изв. АН СССР. Сер. матем.", 1968, т. 32, № 6 с 1323-67; [5] Кострикин А. И., Ш а ф а р е в и ч И. Р., "Изв. АН СССР. Сер. матем.", 1969, т. 33, № 2, с. 252-322; [6] Helgason S., Differential geometry. Lie groups, and symmetric spaces, N. Y., 1978. Э. Б. Винберг.