АЛГЕБРА

- часть математики, посвященная изучению алгебраических операций.

Исторический очерк. Простейшие алгебраич. операции - арифметич. действия над натуральными и положительными рациональными числами - встречаются в самых ранних математич. текстах, свидетельствующих о том, что уже в глубокой древности были известны все основные свойства этих действий. Значительное влияние на развитие алгебраич. идей и символики оказала, в частности, "Арифметика" Диофанта (3 в. н. э.). Термин "А." происходит от названия сочинения Мухаммеда аль-Хорезми "Альджебр аль-мукабала" (9 в.), содержащего общие приемы для решения задач, сводящихся к алгебраич. уравнениям 1-й и 2-й степеней. В конце 15 в. вместо громоздкого словесного описания алгебраич. действий, господствовавшего ранее, в математич. сочинениях появляются принятые теперь знаки + и -, затем знаки степеней, корней, скобки. Ф. Виет ( конец 16 в.) первым стал применять буквенные обозначения как для неизвестных, так и для заданных в задаче величин. К сер. 17 в. в основном сложилась современная алгебраич. символика и тем самым завершилась "предыстория" А. Развитие собственно А. происходило в три последующих столетия, причем точка зрения на ее предмет несколько раз существенно менялась.

В 17-18 вв. под А. понималась наука о буквенных вычислениях - тождественных преобразованиях буквенных формул, решения алгебраических уравнений и т. п., - в отличие от арифметики, занимавшейся вычислениями над конкретными числами. Предполагалось, однако, что под буквами подразумеваются числа, целые или дробные. Вот краткое содержание одного из лучших руководств того времени - "Введения в алгебру" Л. Эйлера (L. Euler): целые числа, обыкновенные и десятичные дроби, корни, логарифмы, алгебра-ич. уравнения 1-й - 4-й степеней, прогрессии, соединения, бином Ньютона, диофантовы уравнения. Таким образом, к сер. 18 в. А. сложилась в том приблизительно объеме, к-рый теперь принято наз. "элементарной" А. А. 18-19 вв. есть прежде всего А. многочленов. Исторически первой задачей А. было решение алгебраич. уравнений с одним неизвестным, т. е. уравнений вида:

Имелось в виду отыскание формул, выражающих корни уравнения через его коэффициенты при помощи сложения, умножения, вычитания, деления и извлечения корней ("решение в радикалах"). С древнейших времен математики умели решать уравнения 1-й и 2-й степеней. В 16 в. существенное продвижение было сделано итальянскими математиками - сначала была найдена формула для решения уравнений 3-й степени (см. Кардана формула), а затем и метод решения (см. Феррари метод).уравнения 4-й степени. В течение почти трех последующих столетий продолжались безуспешные попытки найти аналогичные формулы для решения уравнений высших степеней, в связи с чем приобрела большой интерес задача найти хотя бы "бесформульное" доказательство существования комплексного корня для произвольного алгебраич. уравнения с комплексными коэффициентами. Эта теорема была впервые высказана в 17 в. А. Жираром (A. Girard), но первое строгое доказательство ее дал К. Гаусс (С. Gauss) в конце 18 в. (см. Алгебры основная теорема). Наконец, в 1824 Н. Абель (N. Abel) установил, что уравнения выше 4-й степени в общем случае в радикалах не разрешимы, а в 1830 Э. Галуа (Е. Galois) указал общий критерий разрешимости алгебраич. уравнения в радикалах (см. Галуа теория). Другие задачи отходят в это время на второй план, и под А. понимается "анализ уравнений", как отмечает Ж. Серре (J. Serret) в своем курсе высшей алгебры (1849).

Наряду с теорией алгебраич. уравнений с одним неизвестным развивается теория систем алгебраич. уравнений с несколькими неизвестными, в частности систем линейных уравнений. В связи с исследованием последних возникают понятия матрицы и определителя. В дальнейшем матрицы становятся предметом самостоят, теории - алгебры матриц, роль к-рой не исчерпывается применением к исследованию систем линейных уравнений.

Начиная с сер. 19 в., центр тяжести в алгебраич. исследованиях постепенно перемещается с теории уравнений на изучение произвольных алгебраич. операций. Первоначальные попытки аксиоматич. изучения алгебраич. операций можно проследить уже в "теории отношений" Евклида, однако они не получили развития из-за невозможности геометрически интерпретировать даже простейшие действия над числами как отношениями длин или площадей. Дальнейший прогресс оказался возможным только после постепенного расширения и углубления понятия числа, а также в результате появления разнообразных примеров алгебраич. операций над объектами совсем иной природы, нежели числа,- первыми такими примерами (нач. 19 в.) явились "композиция двоичных квадратичных форм" К. Гаусса и умножение подстановок П. Руффини (P. Ruffini) и О. Коши (A. Cauchy). Явное выделение абстрактного понятия алгебраич. операции было сделано в сер. 19 в. в связи с исследованиями природы комплексных чисел. Возникают алгебра логики Дж. Буля (G. Boole), внешние алгебры Г. Грассмана (Н. Grassmann), кватернионы У. Гамильтона (W. Hamilton). А. Кэли (A. Cayley) создает матричное исчисление, К. Жордан (С. Jordan) публикует большой трактат о группах подстановок.

Эти работы подготовили вступление А. в конце 19 - нач. 20 вв. в современный этап ее развития, характеризующийся объединением ранее разрозненных алгебраич. идей на общей аксиоматич. основе и существенным расширением области приложений А. Современная точка зрения на А. как на общую теорию алгебраич. операций сформировалась в нач. 20 в. под влиянием работ Д. Гильберта (D. Hilbert), Э. Штейница (E.Steinitz), Э. Артина (Е. Artin), Э. Нётер (Е. Noether) и окончательно утвердилась с выходом в 1930 монографии Б. Л. ван дер Вардена (В. L. van der Waerden) "Современная алгебра".

Предмет, основные разделы алгебры, связь с другими областями математики. Предметом изучения современной А. являются множества с заданными на них алгебраич. операциями (т. е. алгебры, или универсальные алгебры, см. терминологич. справку Алгебра), рассматриваемые с точностью до изоморфизма. Последнее означает, что природа множеств - носителей алгебраич. операций с точки зрения А. безразлична, и в этом смысле подлинным объектом изучения являются сами алгебраич. операции (см. начало статьи).

Фактическому изучению долгое время подвергались сравнительно немногие основные типы универсальных алгебр, естественно выделившиеся в ходе развития математики и ее приложений.

Один из наиболее важных и наиболее изученных типов алгебр - группы, т. е. алгебры с одной ассоциативной бинарной операцией, содержащие единицу и для каждого элемента - обратный элемент. Понятие группы явилось исторически первым примером универсальной алгебры и послужило во многих отношениях образцом при перестройке А. и, вообще, математики на рубеже 19-20 вв. Значительно позже началось самостоятельное изучение таких обобщений групп, как полугруппы, квазигруппы и лупы.

Важнейшие типы алгебр с двумя бинарными операциями - кольца и поля. Операции в них обычно наз. сложением и умножением. Кольцо определяется аксиомами абелевой группы для сложения и законами дистрибутивности для умножения относительно сложения (см. Кольца и алгебры). Первоначально изучались лишь кольца с ассоциативным умножением, и это требование ассоциативности иногда даже включают в определение кольца (см. Ассоциативные кольца и алгебры). В настоящее время вполне сложившимся является общее направление, посвященное изучению неассоциативных колец (см. Не ассоциативные кольца и алгебры). Телом наз. ассоциативное кольцо, все отличные от нуля элементы к-рого образуют группу по умножению. Поле- тело с коммутативным умножением. Числовые поля, т. е. совокупности чисел, замкнутые относительно сложения, умножения, вычитания и деления на число, отличное от нуля, неявно фигурировали уже в начальных исследованиях по алгебраич. уравнениям. Ассоциативно-коммутативные кольца и поля являются основными объектами изучения коммутативной алгебры, с к-рой тесно связана алгебраическая геометрия.

Другой важный тип алгебр с двумя бинарными операциями - решетки. Типичные примеры решеток: система подмножеств данного множества с операциями теоретико-множественного объединения и пересечения, множество положительных целых чисел с операциями взятия наименьшего общего кратного и наибольшего общего делителя.

Линейные (или векторные) пространства над полем можно трактовать как универсальные алгебры с одной бинарной операцией - сложением и набором унарных операций - умножений на скаляры из основного поля. Рассматриваются также линейные пространства над телами. Если за множество скаляров взять кольцо, то получается более широкое понятие модуля. Изучению линейных пространств, модулей, а также их линейных преобразований и смежным вопросам посвящен важный раздел А.- линейная алгебра, частью к-рой являются сформировавшиеся еще в 19 в. теория линейных уравнений и теория матриц. К линейной алгебре тесно примыкает полилинейная алгебра.

Первые работы по общей теории произвольных универсальных алгебр (иногда сама эта теория наз. универсальной алгеброй) относятся к 30-м гг. 20 в. и принадлежат Г. Биркгофу (G. Birkhoff). В те же годы А. И. Мальцев и А. Тарский (A. Tarski) заложили основы теории моделей, т. е. множеств с отмеченными на них отношениями. В дальнейшем теория универсальных алгебр и теория моделей столь тесно переплелись между собой, что привели к возникновению новой дисциплины, пограничной между А. и математич. логикой,- теории алгебраических систем, изучающей множества с определенными на них алгебраич. операциями и отношениями.

Ряд дисциплин, пограничных между А. и другими частями математики, определяется внесением в универсальные алгебры дополнительных структур, согласованных с алгебраич. операциями. Сюда относятся топологическая алгебра, в т. ч. теория топологических групп и Ли групп, теория нормированных колец, дифференциальная алгебра, теории различных упорядоченных алгебраич. образований. К сер. 50-х гг. 20 в. оформилась в самостоятельную дисциплину гомологическая алгебра, уходящая своими истоками как в А., так и в топологию.

Роль А. в современной математике исключительно велика, и существует объективная тенденция к дальнейшей "алгебраизации" математики. Типичный путь изучения многих математич. объектов, порой очень далеких от А., состоит в построении алгебраич. систем, достаточно хорошо отражающих поведение изучаемых объектов. Так, изучение групп Ли во многом сводится к изучению их алгебраич. отражений - Ли алгебр. Аналогичный метод используется в топологии - каждому топологич. пространству сопоставляется нек-рым стандартным способом бесконечная серия групп гомологии (см. Гомологии группа), и эти серии алгебраич. отражений позволяют очень точно судить о свойствах самих пространств. Именно с помощью А. сделаны последние крупные открытия в топологии (см. Алгебраическая топология).

Казалось бы, перевод задач на язык А., решение их на этом языке, а затем обратный перевод только усложняют дело. В действительности такой путь оказывается весьма выгодным, а порой и единственно возможным. Объясняется это тем, что алгебраизация позволяет применить для решения задачи не только чисто словесные рассуждения, но и мощный аппарат формальных алгебраич. вычислений, сокрушающий подчас самые сложные препятствия. Эта роль А. в математич. творчестве напоминает роль современных ЭВМ в задачах практики.

Алгебраич. понятия и методы широко применяются в теории чисел (см. Алгебраическая теория чисел), в функциональном анализе, в теории дифференциальных уравнений, в геометрии (см. Инвариантов теория, Проективная геометрия, Тензорная алгебра).и в других математич. дисциплинах.

Наряду с фундаментальной ролью внутри математики А. имеет большое прикладное значение - следует отметить ее выходы в физику (теория представлений конечных групп в квантовой механике, дискретные группы в кристаллографии), в кибернетику (автоматов теория), в математич. экономику ( линейные неравенства).

Лит.:[1] История математики с древнейших времен до начала XIX столетия, т. 1-3, М., 1970-72; [2] Мальцев А. И., К истории алгебры в СССР за первые 2-5 лет, "Алгебра и логика", 1971, т. 10, № 1,с. 103-18; [3] Математика, ее содержание, методы и значение. Сб. статей, т. 1-3, М., 1956; [4] Курош А. Г., Курс высшей алгебры, 10 изд., М., 1971; [5] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962; [6] Вандер Варден Б. Л., Алгебра, пер. с нем., М., 1976; [7] Ленг С., Алгебра, пер. с англ., М., 1968; [8] Мальцев А. И., Алгебраические системы, М., 1970.

См. также лит. при статьях об отдельных алгебраических дисциплинах. Ю. И. Мерзляков, А. И. Ширшов.

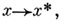
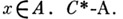С* -АЛГЕБРА - банахова алгебра А над полем комплексных чисел, снабженная такой инволюцией, что норма и инволюция связаны соотношением для любого элемента были введены в 1943 (см. [1]) под назв. вполне регулярных колец, их наз. также 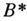-алгебрами.

Важнейшие примеры С*- А . 1) Алгебра непрерывных комплекснозначных функций на локально компактном хаусдорфовом пространстве X, стремящихся к нулю на бесконечности (т. е. таких непрерывных функций f на X, что для любого множество точек удовлетворяющих условию компактно в X); снабжается равномерной нормой

инволюция в определяется как переход к комплексно сопряженной функции: Любая коммутативная С*- А . Аизометрически и симметрически изоморфна С*- А . (т. е. изоморфна как банахова алгебра А с инволюцией) где X - пространство максимальных идеалов алгебры А, снабженное топологией Гельфанда (см. [1], [2], [3]).

2) Алгебра L)Н).всех ограниченных линейных операторов в гильбертовом пространстве Н, рассматриваемая относительно обычных линейных операций и умножения операторов; инволюция в L)Н).определяется как переход к сопряженному оператору, норма - как обычная норма оператора.

Подмножество наз. самосопряженным, если 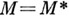, где Любая замкнутая самосопряженная подалгебра В С*- А . А является С*- А . относительно линейных операций, умножения, инволюции и нормы, заимствованных из А; В наз. 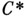-подалгеброй А. Всякая С*- А . изометрически и симметрически изоморфна С*-подалгебре нек-рой С*- А . вида Любой замкнутый двусторонний идеал Iв С*- А . Асамосопряжен (поэтому I есть С*-подалгебра А), факторалгебра 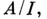снабженная естественными линейными операциями, умножением, инволюцией и нормой факторпространства, есть С*-А. Множество К)Н).вполне непрерывных линейных операторов в гильбертовом пространстве Несть замкнутый двусторонний идеал в L)H). Если Аесть - алгебра с инволюцией, получаемая из Априсоединением единичного элемента, то на существует единственная норма, превращающая в С*-А. и продолжающая норму на А. Кроме того, для С*-А. определены операции ограниченной прямой суммы и тензорного произведения (см. [3], [4]).

Как и во всякой симметричной банаховой алгебре, в С*-А. Аможно выделить подмножества: действительное линейное пространство эрмитовых элементов; множество нормальных элементов; мультипликативную группу Uунитарных элементов (если Асодержит единичный элемент); множество положительных элементов. Множество есть замкнутый конус в и конус превращает в упорядоченное действительное векторное пространство. Если Асодержит единичный элемент 1. то 1 - внутренняя точка конуса Линейный функционал на Аназ. положительным, если для всех такой функционал непрерывен. Если где Весть -подалгебра А, то спектр элемента хв Всовпадает со спектром х в А. Спектр эрмитова элемента действителен, спектр унитарного элемента лежит на единичной окружности, спектр положительного элемента неотрицателен. Построено функциональное исчисление для нормальных элементов С*- А . Любая С*- А . А имеет аппроксимативную единицу, лежащую в единичном шаре алгебры Аи образованную положительными элементами из А. Если - замкнутые двусторонние идеалы в А, то - замкнутый двусторонний идеал в A и J+. Если I - замкнутый двусторонний идеал в J, J - замкнутый двусторонний идеал в А, то I - замкнутый двусторонний идеал в А. Всякий замкнутый двусторонний идеал есть пересечение содержащих его двусторонних примитивных идеалов; всякий замкнутый левый идеал в А - есть пересечение содержащих его максимальных регулярных левых идеалов.

Любой *-изоморфизм С*- А . является изометрическим. Любой *-гомоморфизм 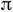банаховой алгебры с инволюцией Вв С*- А . А непрерывен и 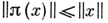для всех В частности, все представления банаховой алгебры с инволюцией (т. е. *-гомоморфизм Вв С*- А . вида непрерывны. Теория представлений С*-А. составляют существенную часть теории С*-А., и приложения теории С*- А . связаны именно с теорией представлений С*-А. Свойства представлений С*- А . позволяют построить для каждой С*- А . А топологич. пространство А, наз. спектром С*-А., и снабдить это пространство Макки борелевской структурой. Спектр С*- А ., вообще говоря, не удовлетворяет никаким аксиомам отделимости, но является локально бикомпактным Бэра пространством.

С*- А. А наз. 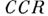- алгеброй (соответственно GCR - алгеброй), если для любого ненулевого неприводимого представления С*- А . А в гильбертовом пространстве Нвыполняется соотношение 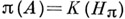(соответственно .

С*- А. <наз. NGCR - алгеброй, если Ане содержит ненулевых замкнутых двусторонних GCR- идеалов (т. е. идеалов, являющихся GCR- алгебрами). Любая С*- А. А содержит максимальный двусторонний GCR- идеал I, и факторалгебра А/I есть NGCR- алгебра. Всякая GCR- алгебра содержит возрастающее семейство замкнутых двусторонних идеалов 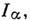занумерованных порядковыми числами 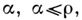такое, что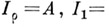 есть GCR - алгебра при всех 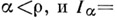для предельных порядковых чисел а. Спектр GCR - алгебры содержит открытое всюду плотное отделимое локально бикомпактное подмножество.

С*- А . А наз. С*-алгеброй типа I, если для любого представления 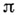С*- А . А в гильбертовом пространстве 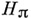Неймана алгебра, порожденная семейством в , есть алгебра Неймана типа I. Для С*-А. Аследующие условия эквивалентны: а) Аесть С*-А. типа I; б) Аесть GCR - алгебра; в) любое факторпредставление С*- А . А кратно неприводимому. Если Аудовлетворяет этим условиям, то: 1) неприводимые представления С*- А . А эквивалентны тогда и только тогда, когда их ядра совпадают; 2) спектр С*- А . А есть Т ₀ пространство. Если А - сепарабельная С*-А., то каждое из условий 1) и 2) эквивалентно условиям а) - в). В частности, всякая сепарабельная С*- А ., имеющая единственное с точностью до эквивалентности неприводимое представление, изоморфна С*-А. К)Н).для нек-рого гильбертова пространства Н.

Пусть Аесть С*- А ., Р- множество таких элементов , что функция конечна и непрерывна на спектре С*- А . А. Если линейная оболочка множества Рвсюду плотна в A, то Аназ. С*-А. с непрерывным следом. Спектр таких С*-А. отделим, и при нек-рых дополнительных условиях С*-А. с непрерывным следом можно представить в виде алгебры вектор-функций на спектре 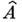(см. [3]).

Пусть Аесть 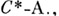F - множество положительных линейных функционалов на Ас нормой Р )А) - множество ненулевых крайних точек выпуклого множества F. Тогда Р)А) - множество чистых состояний А(см. Представления симметричных алгебр]. Пусть Весть С*-подалгебра А. Если Аесть GCR- алгебра и Вразделяет точки множества т. е. для любых существует , такой, что 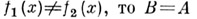(теорема Стоуна - Вейерштрасса). Если А - произвольная С*- А . и В разделяет точки множества то В=А.

Второе сопряженное пространство А** с С*-А. Аестественным образом снабжается операцией умножения, превращающей А** в С*-А., изоморфную нек-рой алгебре Неймана; эта алгебра наз. обертывающей алгеброй Неймана С*- А . (см. [3], [4]).

Теория С*- А . имеет многочисленные применения в теории представлений групп и симметричных алгебр [3], теории динамич. систем [4], статистич. физике и квантовой теории поля [5], а также в теории операторов в гильбертовом пространстве [6].

Лит.:[1] Гельфанд И. М., Наймарк М. А., "Матем сб.", 1943, т. 12, № 2, с. 197-213; [2] Наймарк М. А. Нормированные кольца, М.. 1956; [3] Диксмье Ж., С*-алгебры и их представления, пер. с франц., М., 1974; [4] Saka S., C*-algebras and W*-algebras, N. Y., 1971; [5] Рюэль Д. Статистическая механика. Строгие результаты, пер. с франц. М., 1971; [6] Douglas R. G., Banach Algebra Technigues in Operator Theory, N. Y., 1972. А. И. Штерн.

PI-АЛГЕБРА - алгебра над полем, в к-рой выполняются нек-рые полиномиальные тождества.

Пусть А - ассоциативная алгебра над полем F,

- свободная ассоциативная алгебра (алгебра некоммутативных многочленов) от счетного множества образующих над Fи - ненулевой элемент алгебры F[x]. Тогда

наз. полиномиальным тождеством алгебры А, если для любого набора элементов

Примеры PI-A. и тождеств. В коммутативной алгебре выполняется тождество

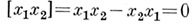
(тождество коммутативности); во внешней алгебре линейного пространства выполняется тождество метабелевости алгебра Аконечной размерности п -1 над полем Fудовлетворяет так наз. стандартному тождеству n-й степени

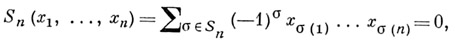
где S_n- группа подстановок множества, состоящего из первых га натуральных чисел л а также более общему тождеству Капелли

в алгебре F_n квадратных матриц порядка n над полем F выполняется стандартное тождество степени 2n. Тензорное произведение PI-A. является PI-A.

Для всякой PI-A. Анад полем Fхарактеристики нуль можно указать такое натуральное число n, что тождества алгебры Аисчерпываются степенями тождеств алгебры матриц F_n , причем нек-рая степень любого тождества алгебры F_n является тождеством алгебры А . Таким образом, во всякой PI-A. над полем характеристики нуль выполняется нек-рая степень стандартного тождества.

Совокупность всех левых частей тождеств, выполняющихся в данной алгебре А, образует вполне харак-теристич. идеал (коротко, Т-идеал).свободной алгебры F[x]и обратно, для всякого Т-идеала существует алгебра, совокупность тождеств к-рой совпадает с этим Т-идеалом (ею будет, напр., факторалгебра F[x]/T). В случае, когда поле Fнулевой характеристики, тождества можно дифференцировать, и Т-идеалы алгебры F[x] - это в точности дифференциально замкнутые односторонние идеалы. Напр., из нильтождества многократным дифференцированием получается тождество

к-рое является полилинейным (точнее, n-линейным), т, е. линейным по каждой переменной, входящей в его запись. Причем и обратно, положив в последнем тождестве 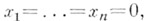можно получить тождество или 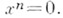Этот процесс линеаризации тождеств позволяет утверждать (в случае полей нулевой характеристики), что все тождества алгебры являются следствиями ее полилинейных тождеств. Для алгебры с единицей, более того, все тождества вытекают из ее полилинейных тождеств, представимых в виде линейных комбинаций произведений правонормированных коммутаторов различных степеней от образующих х;. Вопрос о том, всякая ли ассоциативная алгебра обладает конечным базисом тождеств, составляет содержание проблемы Шпехта.

Совокупность всех алгебр, удовлетворяющих данной системе тождеств, наз. многообразием. Многообразие может быть определено также как класс алгебр, замкнутый относительно взятия подалгебр, гомоморфных образов и подпрямых произведений (см. также Алгебраических систем многообразие). Для ряда многообразий алгебр доказана их конечная базируемость (т. е. в этих многообразиях положительно решена проблема Шпехта). Таковы многообразия (все над полем нулевой характеристики) нильпотентных алгебр данного индекса n, алгебр, в к-рых аддитивные коммутаторы длины правны нулю (Ли - нильпотентные алгебры), многообразие алгебр, определяемое Т-идеалом политождеств -алгебры матриц 2-го порядка. Однако для многообразия, определяемого идеалом тождеств -алгебры матриц порядка вопрос открыт.

Наличие полиномиального тождества жестко определяет структуру ассоциативной алгебры. Примитивная алгебра А, удовлетворяющая полиномиальному тождеству степени d, изоморфна алгебре матриц D_n над телом Dс центром Zи

Поэтому полупростая (в смысле Джекобсона радикала).PI-A. разлагается в подпрямую сумму полных матричных алгебр над телами, причем порядки этих алгебр и размерности тел над центрами ограничены в совокупности, и Т-идеал тождеств полупростой алгебры совпадает с нек-рым "матричным" Т-идеалом М _п . Упорядоченная PI-A. коммутативна. Первичная PI-A. Аобладает двусторонним классич. кольцом частных Q)A), к-рое изоморфно матричной алгебре D_m над телом D, конечномерным над своим центром Z. Кольцо Q)A). является центральным расширением алгебры Ав том смысле, что Идеалы тождеств алгебр Аи Q)A).совпадают. PI-A. удовлетворяют ряду условий "бернсайдовского типа" (см. Бернсайда проблема). Например, алгебраическая (ниль-) PI-A. локально конечна (локально ннльпотентна). Ассоциативная нильалгебра ограниченного индекса пнильпотентна, если характеристика основного поля нулевая или больше n.

PI-A., не имеющая ненулевых нильидеалов, представима матрицами над коммутативным кольцом. Но не всякая Р1-А. представима в таком смысле. Напр., внешняя алгебра счетномерного пространства не представима - в ней не выполняется никакое стандартное тождество. Внутренняя характеризация представимости алгебры матрицами над коммутативным кольцом составляет самостоятельное направление исследований в теории PI-A.

Радикал Джекобсона конечно порожденной PI-A. над полем нулевой характеристики является нильидеалом. Вопрос о его нильпотентности пока (1977) открыт. Если радикал Джекобсона PI-A. нильпотентен, то она удовлетворяет всем тождествам алгебры матриц порядка пдля нек-рого п. Для конечно порожденных алгебр доказано и обратное утверждение. Более того, для конечно порожденной алгебры над полем нулевой характеристики нильпотентность радикала Джекобсона эквивалентна выполнимости в ней нек-рого стандартною тождества.

Во многих случаях выполнимость тождества для "части" элементов алгебры влечет за собой выполнимость нек-рого тождества во всей алгебре. Напр., если в алгебре с инволюцией симметрические элементы удовлетворяют тождеству, то она - PI-A.; если на алгебра над полем нулевой характеристики действует конечная группа автоморфизмов и подалгебра инвариантов удовлетворяет нек-рому тождеству, то исходная алгебра будет PI-A.

Представляет интерес при каких условиях те или иные алгебры специального типа удовлетворяют полиномиальному тождеству.

Для того чтобы групповая алгебра F)G).группы Gнад полем нулевой характеристики удовлетворяла некоторому полиномиальному тождеству, необходимо и достаточно, чтобы группа Gобладала абелевой подгруппой конечного индекса. Если же характеристика Fконечна и равна р, то F[G]является PI-A. тогда и только тогда, когда Gобладает р-абелевой подгруппой конечного индекса (группа наз. р-a белевой, если ее коммутант - конечная р-группа).

Универсальная обертывающая алгебра алгебры Ли Lнад полем Fхарактеристики нуль есть PI-A. в том и только том случае, когда Lабелева (U_L- коммутативна). Если же F - поле конечной характеристики, то 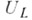является PI-A. тогда и только тогда, когда Lобладает абелевым идеалом конечной коразмерности и присоединенное представление алгебры Lявляется алгебраическим ограниченной степени.

Все Pi-подалгебры свободной ассоциативной алгебры коммутативны.

Теория PI-A. является естественным обобщением коммутативной алгебры, она содержит глубокие и законченные аналоги теорем коммутативной алгебры, что позволяет говорить о зарождении некоммутативной алгебраич. геометрии.

Во всякой конечно порожденной PI-A. А с образующими a₁ ,..., a_k над полем Fвыполняется условие ограниченности высот, т. е. существуют конечное число слов и натуральное число hтакие, что всякое слово и от образующих пред-ставимо в A в виде линейной комбинации слов

где совпадающих по составу относительно со словом В коммутативном случае в качестве слов можно взять сами образующие Свободным некоммутативным аффинным кольцом наз. факторалгебра

где - свободная алгебра с конечным числом образующих x_i над полем Fхарактеристики нуль, а М _п - определенный выше Т-идеал тождеств матричной алгебры f_n . Алгебра есть PI-A. без делителей нуля, она обладает классич. телом частных конечномерным над своим центром Z. Пусть, далее, - пространство, элементами к-рого являются строки длины k, состоящие из матриц алгебры F_n . Можно говорить о нулях элементов алгебры 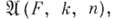лежащих в пространстве об алгеб-раич. многообразиях пространства и т. д. При этом окажутся выполненными основные положения классической алгебраич. геометрии. Так, имеет место некоммутативный аналог Гильберта теоремы о нулях. Неприводимым алгебраич. многообразиям соответствуют первичные идеалы алгебры, удовлетворяющие условию нётеровости. Выполняется теорема Крулля о совпадении максимальной из длин цепочек первичных идеалов алгебры со степенью трансцендентности Zнад F, к-рая в рассматриваемом случае равна

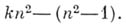
По аналогии с ассоциативными алгебрами можно определить с помощью элементов свободных алгебр PI-A. в других классах алгебр, обладающих свободными алгебрами (лиевы, альтернативные и др.).

Алгебра Ли над полем нулевой характеристики, удовлетворяющая n-му тождеству Энгеля

локально нильпотентна. Вопрос о том, влечет ли тождество Энгеля нильпотентность (проблема Xиггинса), решен положительно лишь для n= 4. Для полей положительной характеристики эта проблема имеет отрицательное решение.