БИКОМПАКТНОЕ РАСШИРЕНИЕ

(би)компактификация, - расширение топологического пространства, являющееся бикомпактным пространством. Б. р. существуют у любого топологич. пространства, у любого T₁ -пространства есть Б. р., являющиеся T₁ -пространствами, но наибольший интерес представляют ха-усдорфовы Б. р., имеющиеся лишь у вполне регулярных пространств. Обычно под Б. р. понимают хаусдорфово Б. р., но иногда полезно рассматривать и произвольные Б. р. П. С. Александров [1] доказал, что всякое локально бикомпактное хаусдорфово пространство одной точкой можно дополнить до бикомпакта (см. Александрова бикомпактное расширение). П. С. Урысор [Я], доказав, что всякое нормальное пространство со счетной базой вкладывается в гильбертов кирпич, установил тем самым, что оно обладает Б. р. счетного веса [2]. Термин "Б. р." впервые ввел А. Н. Тихонов [3], к-рый определил класс вполне регулярных пространств и доказал, что вполне регулярные пространства и только они обладают хаусдорфовыми Б. р., при этом вполне регулярное пространство веса имеет хаусдорфово Б. р. веса .

Два Б. р. пространства Xназ. эквивалентными 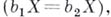если существует гомеоморфизм 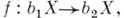тождественный на . Часто Б. р. наз. само отображение вложения: При таком определении два расширения 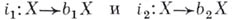будут эквивалентны, если существует такой гомеоморфизм Обычно не различают эквивалентные Б.-р. и наз. Б. р. пространства Xкласс эквивалентных между собой Б. р. этого пространства. В таком случае можно говорить о множестве хаусдорфовых Б. <р. данного (вполне регулярного) пространства X, поскольку мощность любого хаусдорфова расширения пространства Xне больше, чем , а топологии на данном множестве Yтакже образуют множество мощности

Б. р. следует за Б. р. если существует непрерывное отображение тождественное на X. Отношение следования превращает В(X).в частично упорядоченное множество. Э. Чех [4] и М. Стоун [5] доказали, что во множестве В(X).существует наибольший элемент - Стоуна - Чеха бикомпактное расширение (или максимальное Б. р.).

Задача внутреннего описания всех хаусдорфовых Б. <р. данного вполне регулярного пространства Xрешена [6] построением Б. <р. произвольного близости пространства, тем самым показано, что всякой близости на X, совместимой с топологией, соответствует единственное Б. р. X, к-рое индуцирует на Xисходную близость , т. е.

Максимальное Б. р. порождается следующей близостью :

множества Аи Вфункционально отделимы. Б. р. Александрова 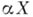локально бикомпактного хаусдорфова пространства Xпорождается близостью : множества Аи Вимеют непересекающиеся замыкания, по крайней мере одно из к-рых бикомпактно.

Соответствие 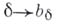является изоморфизмом между частично упорядоченным множеством близостей на X, совместимых о топологией, и множеством В (Х). При этом соответствие 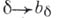продолжается до функтора из категории пространств близости, совместимых с топологическими, и близостно непрерывных отображений в категорию бикомпактов и непрерывных отображений.

Значительная часть теории Б. р. посвящена методам построения Б. <р. А. Н. Тихонов доказал, что во всяком вполне регулярном пространстве Xвеса существует такое семейство функций ~ мощности , что их диагональное произведение осуществляет вложение пространства 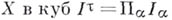(см. Тихоновский куб), после чего Б. р. в Xвеса т получается как замыкание 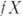в . Э. Чех посредством диагонального произведения всех непрерывных функций построил максимальное Б. <р. пространства X. М. Стоун построил максимальное Б. р. с применением булевых алгебр и колец непрерывных функций.

Одним из основных методов в теории Б. <р. является созданный П. С. Александровым метод центрированных систем открытых множеств [7], вначале использованный для построения максимального Б. р. и впоследствии широко применявшийся многими математиками. Так, было установлено, что всякое хаусдорфово расширение произвольного хаусдорфова пространства Xможно реализовать как пространство центрированных систем открытых в Xмножеств. Метод центрированных систем был применен при построении изоморфизма между множеством близостей на вполне регулярном пространстве и множеством всех его хаусдорфовых Б. р. Этот метод был применен для построения хаусдорфова Б. р. пространств Xпо заданному на нем подчинению.

Г. Уолмен [9] построил максимальное Б. <р. нормального пространства Xкак пространство максимальных центрированных систем замкнутых множеств этого пространства. Пространство максимальных центрированных систем замкнутых множеств -пространства Xявляется его бикомпактным -расширением и наз. Уолмена бикомпактным расширением. Это расширение, как и расширение Стоуна - Чеха, выделяется среди прочих сходством комбинаторного строения с расширяемым пространством, максимальностью (в определенном смысле), возможностью продолжения непрерывных отображений.

Метод центрированных систем замкнутых множеств позволяет дать обобщение расширения Уолмена. Пусть во вполне регулярном пространстве X дана база замкнутых множеств , являющаяся кольцом множеств, т. е. вместе с любыми двумя элементами содержащая их пересечение и объединение. База наз. нормальной, если: 1) для любой точки и всякого не содержащего ее элемента существуют такие элементы базы 2) для любых двух элементов существуют такие элементы что Пространство максимальных центрированных систем нормальной базы-кольца со стандартным заданием на нем базы замкнутых множеств будет хаусдорфовым Б. р. пространства X, наз. расширением уолменовского типа; неизвестно (1977), всякое ли хаусдорфово Б. р. является расширением уолменовского типа.

Другие способы построения Б. р.: метод максимальных идеалов колец непрерывных функций (см. [11]); метод пополнения предкомпактных равномерных структур (см. [12] и Пополнение равномерного пространства);метод проекционных спектров (см. [10]); при этом было доказано, что верхним пределом максимального конечного спектра любого T₁ -пространства Xявляется его уолменовское расширение wХи этот предел совпадает с максимальным Б. р. bХ тогда и только тогда, когда X-квазинормальное пространство.

Важность теории Б. р. объясняется фундаментальным положением бикомпактных пространств в топологии и функциональном анализе. Возможность вложить топологич. пространство в бикомпакт позволяет описать многие свойства вполне регулярных пространств посредством (как правило, более простых) свойств бикомпактов. Так, нормальные пространства с первой аксиомой счетности гомеоморфны тогда и только тогда, когда гомеоморфны их максимальные Б. р. Это позволяет в принципе свести изучение нормальных прост-, ранств с первой аксиомой счетности к изучению бикомпактов. Довольно часто топологич. инварианты расширяемого пространства удается просто выразить в терминах расположения пространства в его Б. <р. (см. Перистое пространство, Полнота, Нормально расположенное подпространство). Так, напр., для того чтобы пространство Xбыло пространством счетного типа, т. е. пространством, в к-ром всякий бикомпакт содержится в бикомпакте счетного характера, необходимо и достаточно, чтобы для нек.-рого (и, следовательно, для всякого) Б. р. нарост был финально компактен. Пространство Xсчетного типа интересно также тем, что оно нормально прилегает к наросту всякого своего Б. р. , т. е. тем, что любые два непересекающиеся замкнутые в наросте множества имеют непересекающиеся в окрестности. С точки зрения расположенности в Б. <р. двойственными к пространствам счетного типа являются финально компактные пространства. Пространство Xфинально компактно тогда и только тогда, когда нек-рое, а значит и всякое, его Б. р. обладает следующим свойством: для всякого бикомпакта 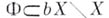в наросте существует содержащий его бикомпакт F, имеющий счетный характер в .

Особенно важна роль Б. р. в теории размерности. Это, в частности, объясняется равенствами

для произвольного нормального пространства Xи равенством

для совершенно нормального пространства Х. Одним из первых утверждений о размерностных свойствах Б. р. явилась теорема о существовании у всякого n-мерного нормального пространства со счетной базой хаусдорфова Б. р. того же (счетного) веса и той же размерности (см. [16]). Доказано [20], что среди нормальных пространств Xсо счетной базой периферически бикомпактное пространство и только оно имеет Б. <р. bХ с нульмерным (в смысле размерности ind) наростом (см. Фрейденталя бикомпактное расширение). При этом среди таких Б. <р. данного пространства существует наибольшее. Эти два результата явились отправной точкой для целого ряда исследований. Так, доказано [8], что для всякого вполне регулярного пространства , в частности для всякого нормального пространства Xвеса существует Б. <р. веса и размерности С другой стороны, вполне регулярное пространство Xпериферически бикомпактно тогда и только тогда, когда Xимеет Б. р. с нульмерно лежащим в нем наростом [8]. При этом нарост нульмерно расположен в расширении , если существует такая база бикомпакта , что

для всех

Видную роль в теории Б. р. играют совершенно бикомпактные расширения (см. [15]). Всякое совершенное Б. <р. пространства Xявляется монотонным образом максимального В. р. (в частности, совершенно и само ), как и , близко к Xпо комбинаторному строению но, в отличие от , не всегда даже для метрич. пространства X. В то время, как есть наибольшее совершенное Б. <р., минимальное совершенное Б. <р. существует лишь тогда, когда пространство Xимеет Б. <р. с нунктиформным наростом (в четности, когда пространство Xпериферически бикомпактно). При этом минимальное совершенное Б. <р. единственно, обладает пунктиформным наростом и является наибольшим среди всех расширений с пунктиформным наростом.

Понятие совершенного Б. р. оказывается полезным при изучении размерности нароста. Если метрич. пространство Xсо счетной базой вкладывается в компакт с наростом размерности ,то в существует такая (открытая) база, что пересечение границ любых ее элементов компактно [15]. Это условие не является достаточным для существования у пространства XБ. <р. bХ с . Более того, если совершенное Б. <р. пространства , для всякого бикомпакта для всякого Б. р. 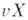с пунктиформным наростом [15]. Совершенное Б. р., как и максимальное, интересно возможностью продолжения отображений. Так, в частности, если пространства обладают минимальными совершенными расширениями 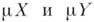, то всякое совершенное отображение продолжается в отображение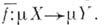

Топологич. пространство веса индуктивно нульмерно (т. е. ) тогда и только тогда (см. [16]), когда оно имеет индуктивно нульмерное Б. <р. bХ веса , так что пространство веса с 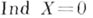имеет Б. <р. того же веса и той же размерности. У вполне регулярного пространства с существует Б. р. причем это верно и для трансфинитных значений . Поэтому у сильно паракомпактного метрич. пространства X существует такое Б. р. 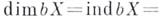, что , , в то же время существует такое пространство X, что для всякого его Б. р. в X (см. [21] ).

Имеется ряд утверждений о Б. <р. бесконечномерных пространств. Так, максимальное Б. <р. нормального S-слабо бесконечномерного пространства Xслабо бесконечномерно [16]. Дадее, любое вполне регулярное пространство X веса , максимальное Б. р. к-рого слабо бесконечномерно (в частности, любое нормальное S- слабо бесконечномерное пространство Xвеса ), обладает слабо бесконечномерным Б. р. веса . В этих утверждениях s-слабую бесконечномерность нельзя заменить на А-слабую бесконечномерность (см. Слабо бесконечномерное пространство):так, все Б. р. растущей суммы кубов (подмножества

гильбертова кирпича, состоящего из точек, у к-рых лишь конечное число координат отлично от нуля) суть сильно бесконечномерные пространства [15].

Исследованы [17] вопросы, касающиеся размерности dim наростов Б. р. пространств близости и вполне регулярных пространств. Если пространство близости нормально прилегает к 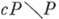, где (единственное) Б. р. пространства Р, то 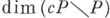равна наименьшему из тех чисел k, что в каждое продолжаемое окаймление можно вписать окаймление кратности (см. Окаймление пространства в расширении). Пространство Xсчетного типа обладает Б. <р. с наростом размерности тогда и только тогда, когда в Xсуществует структура окаймлений кратности обладающая базисным свойством. Кроме того, из существования у данного пространства X Б. <р. с наростом размерности вытекает существование Б. <р. bХ веса 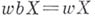с наростом размерности .

Частично упорядоченное множество всех хаусдорфовых Б. <р. пространства Xявляется полной полурешеткой (относительно операции взятия верхней грани). Множество есть (полная) решетка тогда и только тогда, когда пространство Xлокально бикомпактно. Если пространства Xи У локально бикомпактны, то решетки изоморфны тогда и только тогда, когда гомеоморфны наросты (см. [18]). Неизвестны условия, к-рым должно удовлетворять (совершенное) отображение чтобы полурешетки были изоморфны. В то же время Б. р. совершенных неприводимых прообразов пространства Xописываются -близостями на пространстве Xи образуют полную полурешетку относительно естественно определяемого порядка [19]. Б. р. совершенных неприводимых прообразов пространства Xсвязаны также с Я-замкнутыми расширениями пространства X.

Лит.:[1] Александров П. С., Урысон П. С., Мемуар о компактных топологических пространствах, 3 изд., М., 1971; [2] Урысон П. С., Труды по топологии и другим областям математики, т. 1-2, М.- Л., 1951; [3] Тихонов А. Н., "Math. Ann.", 1929, Bd 102, S. 544-61; [4] Cech E., "Ann. Math.", 1937, v. 38, p. 823-44; [5] Stone M., "Trans. Amet. Math. Soc.", 1937, v. 41, p. 375-481; [6] Смирнов Ю. М,, "Матем. сб.", 1952, т. 31, с. 543-74; [7] Александров П. С., "Матем. сб.", 1939, т. 5 [47], с. 403-23; [8] его же, "Успехи матем. науки", 1960, т. 15, в. 2, с. 25-95; [9] Wа11man H., "Ann. Math.", 1941, v. 42 [2], p. 687-97; [10] Зайцев В. И., "Труды Моск. матем. об-ва", 1972, т. 27, с. 129-93; [11] Гельфанд И. М., Райков Д. А., Шилов Г. Е., "Успехи матем. наук", 1946, т. 1, в. 2, е. 48-146; [12] Samuel P., "Trans. Amer. Math. Soc.", 1948, v. 64, p. 100-32; [13] Архангельский А. В., "Матем. сб.", 1973, т. 91, М 1, с. 78-87; [14] Малыхин В., "Докл. АН СССР", 1972; т. 206, № 6, с. 1293- 1296; [15] Александров П. С.."Успехи матем. наук", 1964, т. 19 : 6, с. 3-46; 1965, т. 20, в. 1, с. 253-4; [16] Александров П. С., Пасынков Б. А., Введение в теорию размерности, М., 1973; [17] Смирнов Ю. М., "Матем. сб.", 1966, т. 69, № 1, с. 141-60; 1966, т. 71 : 4, с. 454-82; [18] Мagi11 К. D., "Ргос. London Math. Soc.", 1968, Ser. 3, v. 18, pt 2, p. 231 - 44; [19] Федорчук В. В., "Матем. сб.", 1968, т. 76 : 4, с. 513-36; [20] Freudenthal H., "Ann. Math.", 1942, v. 43, № 2, p. 261-79; [21] Смирнов Ю. М., "Докл. АН СССР", 1957, т. 117, № 6, с. 939-42. В. В. Федорчук.