СТОУНА - ЧЕХА БИКОМПАКТНОЕ РАСШИРЕНИЕ
Смотреть что такое "СТОУНА - ЧЕХА БИКОМПАКТНОЕ РАСШИРЕНИЕ" в других словарях:
БИКОМПАКТНОЕ РАСШИРЕНИЕ — (би)компактификация, расширение топологического пространства, являющееся бикомпактным пространством. Б. р. существуют у любого топологич. пространства, у любого T1 пространства есть Б. р., являющиеся T1 пространствами, но наибольший интерес… … Математическая энциклопедия
СОВЕРШЕННОЕ БИКОМПАКТНОЕ РАСШИРЕНИЕ — расширение Y вполне регулярного пространства X такое, что замыкание в Yграницы любого открытого множества служит границей O(U), где O(U) максимально открытое в У множество, для к рого Эквивалентные требования: а) для любой пары непересекающихся… … Математическая энциклопедия
УОЛМЕНА БИКОМПАКТНОЕ РАСШИРЕНИЕ — (правильнее Уолмена Шанина бикомпактное расширение) топологического пространства X, удовлетворяющего аксиоме T1 (см. Отделимости аксиомы),определяется как множество, точками к рого являются максимальные центрированные системы замкнутых в… … Математическая энциклопедия
АБСОЛЮТ — 1) А. регулярного топологического пространства X пространство аХ, обладающее тем свойством, что оно совершенно и неприводимо отображается на X, а всякий совершенный неприводимый прообраз пространства аХ гомеомор фен пространству аХ. У каждого… … Математическая энциклопедия
ЗАМКНУТОЕ ОТОБРАЖЕНИЕ — отображение одного топологич. пространства на другое, при к ром образ всякого замкнутого множества есть замкнутое множество. Класс непрерывных 3. о. играет важную роль в общей топологии и ее приложениях. Непрерывные замкнутые бикомпактные… … Математическая энциклопедия
ВПОЛНЕ РЕГУЛЯРНОЕ ПРОСТРАНСТВО — топологическое пространство, в к ром всякие два множества, из к рых одно замкнуто, а другое состоит лишь из одной точки, функционально отделимы (см. Отделимости аксиомы). В. р. п., в к рых все одноточечные множества замкнуты (т. е. вполне… … Математическая энциклопедия
РАЗМЕРНОСТЬ — топологического пространства X целочисленный инвариант dim X, определяемый следующим образом. Тогда и только тогда dim X = 1, когда . О непустом тополо гич. пространстве Xговорят, что оно не более чем n мерно, и пишут dim , если в любое конечное… … Математическая энциклопедия
БЛИЗОСТИ ПРОСТРАНСТВО — множество Рс бинарным отношением на множестве всех его подмножеств, удовлетворяющее следующим аксиомам: 1) равносильно (симметричность); 2) равносильно или (аддитивность); 3) равносильно … Математическая энциклопедия
ПРОЕКЦИОННЫЙ СПЕКТР — индексированное направленным множеством( А, >) семейство симплициальных комплексов такое, что для каждой пары индексов , для к рых a >a, определено симплициальное отображение (проекция) комплексов Na на комплекс Na. При этом требуется,… … Математическая энциклопедия
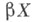вполне регулярного топологич. пространства X. Построено Э. Чехом [1] и М. Стоуном [2]. 
- множество всех непрерывных функций 
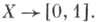Отображение 
где 
является гомеоморфизмом на свой образ. Тогда, но определению, 
(где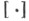 
- операция замыкания). Для любого бикомпактного расширения bХ существует непрерывное отображение 
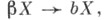тождественное на X, что и выражается эпитетом лнаибольшее