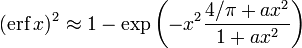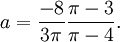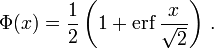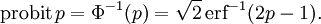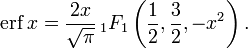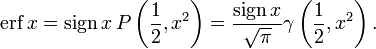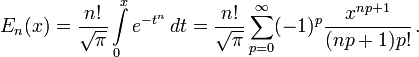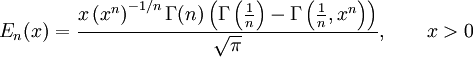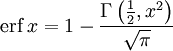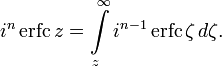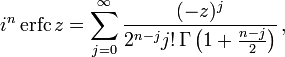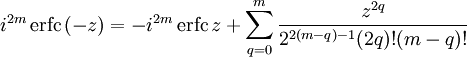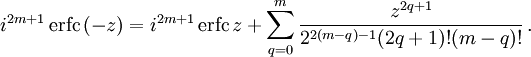- Интеграл вероятности
-
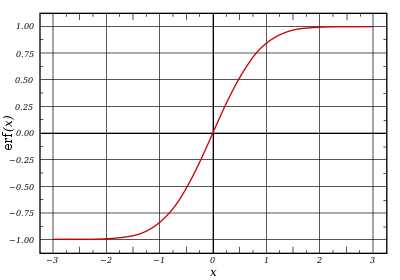 График функции ошибок
График функции ошибокВ математике функция ошибок — это неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Она определяется как
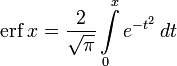 .
.
Дополнительная функция ошибок, обозначаемая
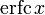 (иногда применяется обозначение
(иногда применяется обозначение 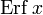 , определяется через функцию ошибок:
, определяется через функцию ошибок: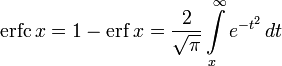 .
.
Комплексная функция ошибок, обозначаемая w(x), также определяется через функцию ошибок:
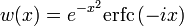 .
.
Содержание
Свойства
- Функция ошибок нечётна:
- Для любого комплексного x выполняется
где черта обозначает комплексное сопряжение числа x.
- Функция ошибок не может быть представлена через элементарные функции, но, разлагая интегрируемое выражение в ряд Тейлора и интегрируя почленно, мы можем получить её представление в виде ряда:
Это равенство выполняется (и ряд сходится) как для любого вещественного x, так и на всей комплексной плоскости. Последовательность знаменателей образует последовательность A007680 в OEIS.
- Для итеративного вычисления элементов ряда полезно представить его в альтернативном виде:
поскольку
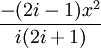 — сомножитель, превращающий i-й член ряда в (i + 1)-й, считая первым членом x.
— сомножитель, превращающий i-й член ряда в (i + 1)-й, считая первым членом x.- Функция ошибок на бесконечности равна единице; однако это справедливо только при приближении к бесконечности по вещественной оси, так как:
- При рассмотрении функции ошибок в комплексной плоскости точка
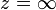 будет для неё существенно особой.
будет для неё существенно особой.
- Производная функции ошибок выводится непосредственно из определения функции:
- Обратная функция ошибок представляет собой ряд
где c0 = 1 и
Поэтому ряд можно представить в следующем виде (заметим, что дроби сокращены):
Последовательности числителей и знаменателей после сокращения — A092676 и A132467 в OEIS; последовательность числителей до сокращения — A002067 в OEIS.
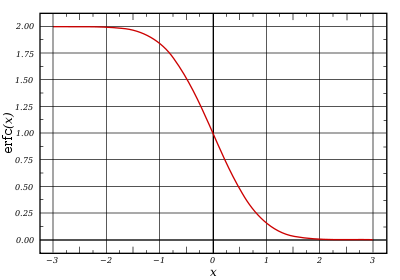 Дополнительная функция ошибок
Дополнительная функция ошибокПрименение
Если набор случайных чисел подчиняется нормальному распределению со стандартным отклонением σ, то вероятность, что число отклонится от среднего не более чем на a, равна
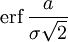 .
.Функция ошибок и дополнительная функция ошибок встречаются в решении некоторых дифференциальных уравнений, например, уравнения теплопроводности с граничными условиями описываемыми функцией Хевисайда («ступенькой»).
В системах цифровой оптической коммуникации, вероятность ошибки на бит также выражается формулой, использующей функцию ошибок.
Асимптотическое разложение
При больших x полезно асимптотическое разложение для дополнительной функции ошибок:
Хотя для любого конечного x этот ряд расходится, на практике первых нескольких членов достаточно для вычисления
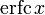 с хорошей точностью, в то время как ряд Тейлора сходится очень медленно.
с хорошей точностью, в то время как ряд Тейлора сходится очень медленно.Другое приближение даётся формулой
где
Родственные функции
С точностью до масштаба и сдвига, функция ошибок совпадает с нормальным интегральным распределением, обозначаемым Φ(x)
Обратная функция к Φ, известная как нормальная квантильная функция, иногда обозначается
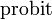 и выражается через нормальную функцию ошибок как
и выражается через нормальную функцию ошибок какНормальное интегральное распределение чаще применяется в теории вероятностей и математической статистике, в то время как функция ошибок чаще применяется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера, а также может быть представлена как вырожденная гипергеометрическая функция (функция Куммера):
Функция ошибок выражается также через интеграл Френеля. В терминах регуляризованной неполной гамма-функции P и неполной гамма-функции,
Обобщённые функции ошибок
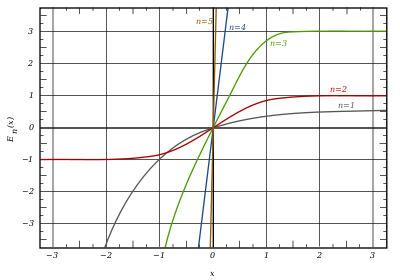 График обобщённых функций ошибок En(x):
График обобщённых функций ошибок En(x):
серая линия: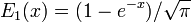
красная линия: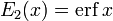
зелёная линия: E3(x)
синяя линия: E4(x)
жёлтая линия: E5(x).Некоторые авторы обсуждают более общие функции
Примечательными частными случаями являются:
- E0(x) — прямая линия, проходящая через начало координат:
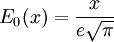
- E2(x) — функция ошибок
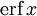 .
.
После деления на n! все En с нечётными n выглядят похоже (но не идентично). Все En с чётными n тоже выглядят похоже, но не идентично, после деления на n!. Все обощённые функции ошибок с n > 0 выглядят похоже на полуоси x > 0.
На полуоси x > 0 все обобщённые функции могут быть выражены через гамма-функцию:
Следовательно, мы можем выразить функцию ошибок через гамма-функцию:
Итерированные интегралы дополнительной функции ошибок
Итерированные интегралы дополнительной функции ошибок определяются как
Их можно разложить в ряд:
откуда следуют свойства симметрии
и
Реализация
В стандартах языков Си и C++ функция ошибок
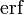 и дополнительная функция ошибок
и дополнительная функция ошибок 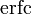 отсутствуют в стандартной библиотеке. Однако в GCC (GNU Compilier Collection) эти функции реализованы как
отсутствуют в стандартной библиотеке. Однако в GCC (GNU Compilier Collection) эти функции реализованы как double erf(double x)иdouble erfc(double x). Функции находятся в заголовочных файлахmath.hилиcmath. Там же есть пары функцийerff(),erfcf()иerfl(),erfcl(). Первая пара получает и возвращает значения типаfloat, а вторая — значения типаlong double. Соответствующие функции также содержатся в библиотеке Math проекта Boost.В языке [2]. Класс
Erfесть в пакетеorg.apache.commons.math.specialот [3]. Однако эта библиотека не является одной из стандартных библиотек Java 6.Matlab[4] и
В языке Special проекта scipy [5].
См. также
- Функция Гаусса
Литература
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (См. часть 7)
Внешние ссылки
Wikimedia Foundation. 2010.

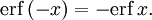
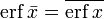
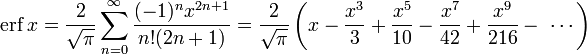
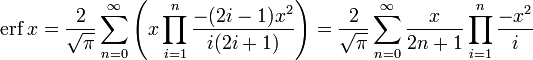
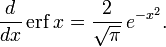
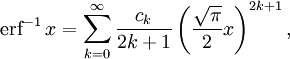
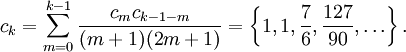
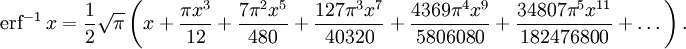
![\operatorname{erfc}\,x = \frac{e^{-x^2}}{x\sqrt{\pi}}\left [1+\sum_{n=1}^\infty (-1)^n \frac{1\cdot3\cdot5\cdots(2n-1)}{(2x^2)^n}\right ]=\frac{e^{-x^2}}{x\sqrt{\pi}}\sum_{n=0}^\infty (-1)^n \frac{(2n)!}{n!(2x)^{2n}}.\,](/pictures/wiki/files/50/2d5fe0b0f05b66753a4dc4d68612c2e1.png)