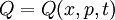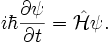- Интеграл движения
-
В механике любая функция
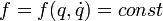 называется интегралом движения, где q — обобщённые координаты,
называется интегралом движения, где q — обобщённые координаты, 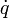 — обобщённые скорости системы.
— обобщённые скорости системы.Интегралы движения, обладающие аддитивностью или асимптотической аддитивностью, называются законами сохранения.
Содержание
Применение
Интегралы движения полезны потому, что некоторые свойства этого движения можно узнать даже без интегрирования уравнений движения. В наиболее успешных случаях траектории движения представляют собой пересечение изоповерхностей соответствующих интегралов движения. Например, построение Пуансо показывает, что без крутящего момента вращение твердого тела представляет собой пересечение сферы (сохранение полного углового момента) и эллипсоида (сохранение энергии), траекторию, которую трудно вывести и визуализировать. Поэтому, нахождение интегралов движения — важная цель в механике.
Методы нахождения интегралов движения
Существует несколько методов нахождения интегралов движения:
- Наиболее простой, но и наименее строгий метод заключается в интуитивном подходе, часто основанном на экспериментальных данных и последующего математического доказательства сохранения величины.
- Уравнение Гамильтона — Якоби предлагает строгий и прямой метод нахождения интегралов движения, особенно если гамильтониан принимает знакомую функциональную форму в ортогональных координатах.
- Другой подход заключается в сопоставлении сохраняющейся величины и какой-либо симметрии Лагранжиана. Теорема Нётер даёт систематический способ вывода таких величин из симметрий. Например, закон сохранения энергии является результатом того, что лагранжиан не изменяется относительно сдвига по времени, закон сохранения импульса эквивалентен инвариантности лагранжиана относительно сдвига начала координат в пространстве (трансляционная симметрия) и закон сохранения момента импульса следует из изотропности пространства (лагранжиан не меняется при поворотах системы координат). Обратное тоже верно: каждая симметрия лагранжиана соответствует интегралу движения.
- Величина A сохраняется если она не зависит явным образом от времени и её скобки Пуассона с гамильтонианом системы равны нулю
Другой полезный результат известен как теорема Пуассона, в которой утверждается, что если есть два интеграла движения A и B то скобки Пуассона {A,B} этих двух величин тоже является интегралом движения.
Система с n степенями свободы и n интегралами движения, такими, что скобки Пуассона любой пары интегралов равны нулю известна как полностью интегрируемая система. Такой набор интегралов движения, как говорят, находится в инволюции друг с другом.
В квантовой механике
Наблюдаемая величина Q сохраняется, если она коммутирует с гамильтонианом H, который не зависит явным образом от времени. Поэтому
где используется коммутационное соотношение
![[\hat \mathcal H,\hat Q] = \hat \mathcal H \hat Q - \hat Q \hat \mathcal H \,](/pictures/wiki/files/50/23d8e83673ecf5f854faa6073c7a27f0.png) .
.
Вывод
Пусть имеется некоторая наблюдаемая Q, которая зависит от координаты, импульса и времени
а также имееется волновая функция, которая является решением соответствующего уравнения Шрёдингера
Для вычисления производной по времени от среднего значения наблюдаемой Q используется правило дифференцирования произведения, и результат после некоторых манипуляций приведён ниже
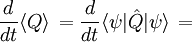
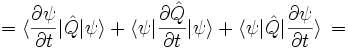
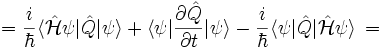
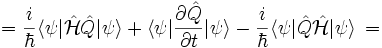
![= \frac{i}{\hbar} \langle \psi|\left[\hat \mathcal H,\hat Q\right]|\psi \rangle + \langle \psi | \frac{\partial \hat Q}{\partial t} | \psi \rangle \, =](/pictures/wiki/files/101/e645564464ebe396c1411295a8154ece.png)
В итоге получим
![\frac{d}{dt} \hat Q = \frac{i}{\hbar} \left[ \hat \mathcal H,\hat Q \right] + \frac{\partial \hat Q}{\partial t} \,](/pictures/wiki/files/98/bb3fdfbf49ce253f9419b55c441ea365.png)
Отношение к квантовому хаосу и квантовой интегрируемости
В классической механике имеется теорема Лиувилля, согласно которой система, в которой число интегралов движения в инволюции совпадает с числом степеней свободы n, может быть полностью проинтегрирована (решена) методом разделения переменных в уравнении Гамильтона—Якоби. Такая система является интегрируемой системой. Траектория такой системы в 2n-мерном фазовом пространстве может быть представлена в подходящих переменных (переменных действие-угол) как намотка на n-мерном торе. Системы, число интегралов в которой меньше числа степеней свободы, проявляет хаотическое поведение, то есть траектории в фазовом пространстве с близкими начальными условиями могут экспоненциально расходиться. При небольшой деформации интегрируемой системы в неинтегрируемую n-мерный тор в 2n-мерном фазовом пространстве разрушается («размывается»), превращаясь, например в странный аттрактор.
Квантовый аналог теоремы Лиувилля неизвестен, однако и в квантовом случае системы можно разделить на интегрируемые и неинтегрируемые. Под интегрируемыми в этом случае подразумевают системы, которые допускают точное решение, в смысле возможности найти все собственные значения и собственные функции гамильтониана в разумном виде. Известен квантовый аналог метода разделения переменных, однако его применение не столь универсально в классических случаях. Изветсные примеры показывают, что в квантовых интегрируемых системах, также как и в классических, имеется n интегралов движения, коммутирующих между собой. Однако наличие n интегралов движения, по-видимому, ещё не гарантирует квантовой интегрируемости. Задача квантования интегрируемых систем представляет собой поиск такой квантовой системы, которая допускала бы точное решение и давала бы данную классическую систему в классическом пределе. Имеются также примеры интегрируемых квантовых систем, не имеющих интегрируемых классических аналогов. Это происходит в том случае, если система может быть решена при специальных значениях параметров квантового гамильтониана, либо когда система не допускает классического описания (как, например, система спинов).
Все остальные квантовые системы проявляют в той или иной степени признаки квантового хаоса. Классические хаотические системы допускают квантование в том смысле, что может быть корректно определено их пространство состояний и гамильтониан, однако как и классические хаотические системы, так и квантовые, по-видимому, не допускают точного решения. Их можно исследовать приближёнными методами, такими как теория возмущений и вариационный метод, а также исследованы численно методами молекулярной динамики в классическом случае или численной диагонализации гамильтониана в квантовом случае.
См. также
Литература
- Introduction to Quantum Mechanics (2nd ed.). — Prentice Hall, 2004. — ISBN ISBN 0-13-805326-X
- Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 4-е, исправленное. — М.: Наука, 1988. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9
- Арнольд В. И. «Математические методы классической механики», из. 5-ое, М.:Едиториал УРСС, 2003, ISBN 5-354-00341-5
Wikimedia Foundation. 2010.

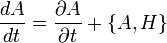
![\frac{d}{dt} \langle \psi | \hat Q | \psi \rangle = \frac{i}{\hbar} \langle \psi|\left[ \hat \mathcal H,\hat Q \right]|\psi \rangle + \langle \psi | \frac{\partial \hat Q}{\partial t} | \psi \rangle \,](/pictures/wiki/files/101/ed7f296870fbf24bd904953f1c7c7f61.png)