- Гёльдера неравенство
-
Нера́венство Гёльдера в функциональном анализе и смежных дисциплинах — это фундаментальное свойство пространств Lp.
Содержание
Формулировка
Пусть
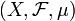 — пространство с мерой, а
— пространство с мерой, а 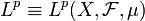 — пространство функций вида
— пространство функций вида 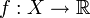 с конечной интегрируемой p-ой степенью. Тогда в последнем определена норма
с конечной интегрируемой p-ой степенью. Тогда в последнем определена норма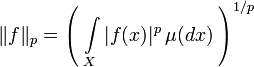 .
.
где
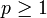 , обычно подразумевается, что это натуральное число.
, обычно подразумевается, что это натуральное число.
Пусть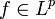 , а
, а 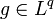 , где
, где 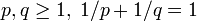 . Тогда
. Тогда 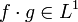 , и
, и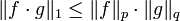 .
.
Частные случаи
Неравенство Коши — Буняковского
Положив p = q = 2, получаем неравенство Коши — Буняковского для пространства L2.
Евклидово пространство
Рассмотрим Евклидово пространство
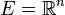 или
или 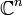 . Lp-норма в этом пространстве имеет вид:
. Lp-норма в этом пространстве имеет вид: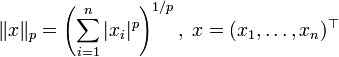 ,
,
и тогда
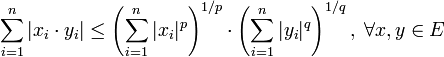 .
.
Пространство lp
Пусть
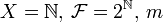 — счётная мера на
— счётная мера на 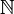 . Тогда множество всех последовательностей
. Тогда множество всех последовательностей 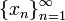 , таких что
, таких что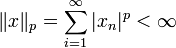 ,
,
называется lp. Неравенство Гёльдера для этого пространства имеет вид:
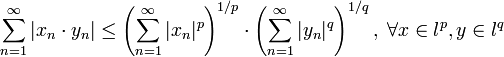 .
.
Вероятностное пространство
Пусть
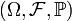 — вероятностное пространство. Тогда
— вероятностное пространство. Тогда 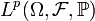 состоит из случайных величин с конечным p-м моментом:
состоит из случайных величин с конечным p-м моментом: ![\mathbb{E}\left[|X|^p\right] < \infty](/pictures/wiki/files/57/982b2f1d6dfcf757eddc7f04e60063ba.png) , где символ
, где символ 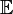 обозначает математическое ожидание. Неравенство Гёльдера в этом случае имеет вид:
обозначает математическое ожидание. Неравенство Гёльдера в этом случае имеет вид: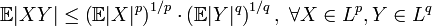 .
.
См. также
- Пространство Lp
- Гёльдер, Отто
- Неравенство Юнга
- Неравенство Минковского
Ссылки
Wikimedia Foundation. 2010.
