- ГЁЛЬДЕРА НЕРАВЕНСТВО
- 1) Г. н. для сумм. Пусть
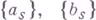 - нек-рые множества комплексных чисел,
- нек-рые множества комплексных чисел,  , где S - конечное или бесконечное множество индексов. Справедливо Г. н.
, где S - конечное или бесконечное множество индексов. Справедливо Г. н.

где
 причем равенство достигается тогда и только тогда, когда
причем равенство достигается тогда и только тогда, когда  , а
, а  и Сне зависят от
и Сне зависят от  . При
. При  Г. н. для сумм наз. Коши неравенством. В предельном случае при
Г. н. для сумм наз. Коши неравенством. В предельном случае при  ,
,  Г. н. имеет вид
Г. н. имеет вид
При
 знак Г. н. меняется на обратный. Г. н. для сумм допускает обращение (М. Рисе, М. Riesz): если
знак Г. н. меняется на обратный. Г. н. для сумм допускает обращение (М. Рисе, М. Riesz): если

при всех
 таких, что то
таких, что то

Для сумм более общего вида Г. н. имеет вид

если

2) Г. н. для интегралов. Пусть S - измеримое по Лебегу множество n-мерного евклидова пространства
 и функции
и функции

принадлежат
 , причем выполнено условие (2). Тогда справедливо Г. н.
, причем выполнено условие (2). Тогда справедливо Г. н.

При
 это есть Буняковского неравенство. Для интегрального Г. н. справедливы замечания (о предельном случае и о знаках), аналогичные замечаниям для Г. н. (1).
это есть Буняковского неравенство. Для интегрального Г. н. справедливы замечания (о предельном случае и о знаках), аналогичные замечаниям для Г. н. (1).
В Г. н. множество S может быть любым множеством, на некоторой алгебре подмножеств которого задана конечно аддитивная функция
 (например, мера), а функции
(например, мера), а функции  -измеримы и
-измеримы и  -интегрируемы в степени
-интегрируемы в степени  .
.
3) Обобщенное Г. н. Пусть S - произвольное множество и пусть на совокупности всех положительных числовых функций
 :
:  задан (конечный или бесконечный) функционал
задан (конечный или бесконечный) функционал  удовлетворяющий условиям: а)
удовлетворяющий условиям: а)  б)
б)  для всех чисел
для всех чисел  в) при
в) при  выполняется неравенство
выполняется неравенство  г)
г) 
Если при этом выполняются условия (2), то справедливо обобщенное Г. н. для функционала:

Лит.:[1] Ноldеr О., "Nachr. Gcs. Wiss. Gottingen", 1889, № 2, p. 38-47; [2] Xapди Г. Г., Литтльвуд Д. Е., Полна Г., Неравенства, пер. с англ., М., 1948: [3] Беккенбах Э., Беллман Р., Неравенства, пер. с англ., М., 1965. Л. П. Купцов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
