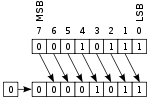
- Булевы операции
-
Битовые операции, иногда также булевы или логические операции[1] — операции над битами, применяемые в программировании и цифровой технике, изучаемые в дискретной математике и математической логике.
Содержание
Введение
Булевы операции и математическая логика
Булевы операции очень близки (хотя и не тождественны) логическим связкам в классической логике. Бит можно рассматривать как логическое суждение — его значениями являются 1 «истина» и 0 «ложь». При такой интерпретации известные в логике связки конъюнкции, дизъюнкции, импликации, отрицания и другие имеют представление на языке битов. И наоборот, битовые операции легко описываются на языке исчисления высказываний.
Однако, связкам математической логики более соответствуют логические операции в т.ч. в программировании, нежели собственно битовые операции.
Булевы операции как основа цифровой техники
Булевы операции лежат в основе обработки цифровых сигналов. А именно, посредством них мы можем из одного или нескольких сигналов на входе получить новый сигнал, который в свою очередь может быть подан на вход одной или нескольким таким операциям. По сути, именно булевы операции в сочетании с запоминающими элементами (напр. триггерами) реализуют всё богатство возможностей современной цифровой техники.
Список битовых операций
И

«(Логическое) И» (and) — аналог конъюнкции в логике. Иногда называется логическим умножением.
В булевой логике: 
В языке C: &Выдаёт 1 если оба входа равны 1, в противном случае 0. Если один из аргументов равен 1, то результат «И» равен другому. Если один из аргументов равен 0, то результат «И» равен 0 независимо от значения другого аргумента.
НЕ
«(Логическое) НЕ» (not), инвертирование — аналог отрицания в логике.
В булевой логике: 
В языке C: ~Данная унарная операция (с одним входом) заменяет 0 на 1 и наоборот. Реализующий её элемент называется инвертором.
ИЛИ

«(Логическое) ИЛИ» (or) — аналог дизъюнкции в логике.
В булевой логике: 
В языке C: |Выдаёт 1 если и только если хотя бы один из входов равен 1. Операция, двойственная AND: при инвертировании выхода и всех входов (т.е. при замене 0 и 1 местами) «И» и «ИЛИ» взаимно превращается друг в друга.
Исключающее ИЛИ
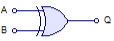
«Исключающее ИЛИ» (xor), «сложение по модулю 2» — аналог исключающего ИЛИ в логике.
В булевой логике: 
В языке C: ^Если один из аргументов равен 0, то результат равен другому. Если один из аргументов равен 1, то результат равен отрицанию другого аргумента. Первое русское название операции обусловлено тем, что результат данной операции отличается от результата «ИЛИ» только в одном случае из 4 случаев входа — обоих 1 (случай одновременной истинности аргументов «исключается»). Ещё в русской грамматике значение данной логической связки передаётся союзом «либо».
Второе название — тем, что действительно является сложением в кольце вычетов по модулю 2, из чего следуют некоторые интересные свойства. Например, в отличие от вышеописанных «И» и «ИЛИ» данная операция является обратимой, или инволютивной:
 .
.В графике «исключающее ИЛИ» применяется при выводе спрайтов на картинку — повторное её применение убирает спрайт с картинки. Благодаря инволютивности же эта операция нашла применение в криптографии как простейшая реализация идеального шифра (шифра Вернама). «Исключающее ИЛИ» также может использоваться для обмена двух переменных, используя алгоритм обмена при помощи исключающего ИЛИ.
Операции от многих аргументов
Операции «И», «ИЛИ» и «исключающее ИЛИ» являются не только коммутативными, но и ассоциативными, и потому легко обобщаются на случай нескольких аргументов (входов).
Прочие бинарные операции
«ИЛИ-НЕ» (nor), она же «стрелка Пирса».
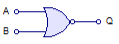
В булевой логике: 
Стрелка Пирса является результатом инвертирования результата «ИЛИ» своих аргументов, выдаёт значение 1 только когда оба входа 0.
«И-НЕ» (nand), или «штрих Шеффера».

В булевой логике: 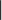
Двойственная стрелке Пирса операция: является результатом инвертирования результата «И» своих аргументов, выдаёт значение 0 только когда оба входа 1. Известна простотой реализации в ТТЛ.
Импликация («если-то») — аналог импликации в логике.В булевой логике: 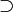
Совпадает с «ИЛИ» с инвертированным первым аргументом, выдаёт значение 0 только когда первый вход 1 а второй — 0. Данная операция не является коммутативной, в отличие от всех вышеописанных бинарных операций. Её можно понимать как арифметическое
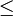 (меньше или равно).
(меньше или равно).
Эквиваленция. Выдаёт 1 если и только если оба аргумента равны между собой. Является результатом инвертирования результата «исключающего ИЛИ» своих аргументов. Она же и двойственна исключающему «ИЛИ» в вышеописанном смысле.Сводная таблица истинности булевых операций
Название→
АргументыИ (AND) НЕ (NOT) ИЛИ (OR) искл. ИЛИ(XOR) импликация стрелка
Пирсаштрих
Шеффераx y ( 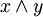 )
)
(x&y)( 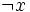 )
)
(~x)( 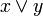 )
)
(x|y)( 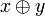 )
)
(x^y)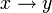 (
(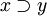 )
)
((~x)|y)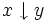
((~x)&(~y))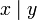
(~(x&y))0 0 0 1 0 0 1 1 1 0 1 0 1 1 1 1 0 1 1 0 0 0 1 1 0 0 1 1 1 1 0 1 0 1 0 0 Операции над битовыми векторами
Обобщение операций на булеву алгебру
Вместо одиночных битов мы можем рассмотреть векторы из фиксированного количества битов (в программировании их называют регистрами), например, байты. В программировании регистры рассматривают как двоичное разложение целого числа: b = b0 + 2b1 + 22b2 + ... + 2N − 1bN − 1, где N — количество битов в регистре.
Тем не менее, ничто не мешает рассматривать эти регистры именно как битовые векторы и проводить булевые операции покомпонентно (бит номер k значения есть результат операция от битов номер k аргументов). Кстати, математически говоря, булевы операции распространяются таким образом на произвольную булеву алгебру. Таким образом мы получаем операции побитового И, ИЛИ, НЕ, искл. ИЛИ и т. д. Как арифметические, данные операции не обладают хорошими свойствами за исключением побитового НЕ, которое для чисел в дополнительном коде совпадает с вычитанием из −1 (
~x == -1-x). Однако, они очень полезны в программировании.Битовые сдвиги
К битовым операциям также относят битовые сдвиги. При сдвиге значения битов копируются в соседние по направлению сдвига. Различают несколько видов сдвигов — логический, арифметический и циклический, в зависимости от обработки крайних битов.
Также различают сдвиг влево (в направлении от младшего бита к старшему) и вправо (в направлении от старшего бита к младшему).
 Арифметический сдвиг (правый)
Арифметический сдвиг (правый) Циклический сдвиг
Циклический сдвиг Циклический сдвиг через перенос
Циклический сдвиг через переносЛогический сдвиг
При логическом сдвиге значение последнего бита по направлению сдвига теряется (копируясь в бит переноса), а первый приобретает нулевое значение.
Логические сдвиги влево и вправо используются для быстрого умножения и деления на 2, соответственно.
Арифметический сдвиг
Арифметический сдвиг аналогичен логическому, но значение слова считается знаковым числом представленному дополнительным кодом. Так при правом сдвиге старший бит сохраняет свое значение. Левый арифметический сдвиг идентичен логическому.
Циклический сдвиг
При циклическом сдвиге, значение последнего бита по направлению сдвига копируется в первый бит (и копируется в бит переноса).
Также различают циклический сдвиг через бит переноса — при нем первый бит по направлению сдвига получает значение из бита переноса, а значение последнего бита сдвигается в бит переноса.
2-адическая интерпретация
Целое число, записанное (в дополнительном коде) в бесконечный (в сторону положительных степеней двойки) двоичный регистр является естественным объектом для теории p-адических чисел при p = 2. Множество целых 2-адических чисел (т.е. произвольных бесконечных битовых последовательностей) может быть рассмотрено как булева алгебра точно так же как и множество значений битового регистра конечной длины. Все вышеперечисленные битовые операции оказываются непрерывными отображениями. Хотя практическое программирование не располагает регистрами бесконечной длины, это не мешает использовать данный теоретический факт в криптографии для создания быстродействующих алгоритмов шифрования.
Практические применения
Физическая реализация битовых операций
Реализация битовых операций может в принципе быть любой: механической, электромеханической, гидравлической, пневматической, оптической и даже химической.
В первой половине XX века вместо транзисторов применяли электромеханические реле и электронные лампы.
В пожароопасных и взрывоопасных условиях до сих пор применяют пневматические логические устройства (пневмоника).
Наиболее распространены электронные реализации битовых операций при помощи транзисторов, например резисторно-транзисторная логика (РТЛ), диодно-транзисторная логика (ДТЛ), эмиттерно-связанная логика (ЭСЛ), транзисторно-транзисторная логика (ТТЛ), N-МОП логика, КМОП логика и др..
В квантовых вычислениях из перечисленных булевых операций реализуются только НЕ и искл. ИЛИ (с некоторыми оговорками). Квантовых аналогов И, ИЛИ и т.д. не существует.
Схемы аппаратной логики
Результат операции ИЛИ-НЕ или ИЛИ ото всех битов двоичного регистра проверяет, равно ли значение регистра нулю; то же самое взятое от выхода искл. ИЛИ двух регистров проверяет равенство их значений между собой.
Битовые операции применяются в знакогенераторах и графических адаптерах; особенно велика была их роль в адаптере графический ускоритель.
Использование в программировании
Благодаря реализации в арифметическом логическом устройстве (АЛУ) процессора многие их регистровые битовые операции аппаратно доступны в языках низкого уровня. В большинстве процессоров реализованы в качестве инструкции регистровый НЕ; регистровые двухаргументные И, ИЛИ, исключающее ИЛИ; проверка равенства нулю (см. выше); три типа битовых сдвигов, а также циклические битовые сдвиги.
Регистровая операция И используется для сброса конкретных битов по битовой маске, ИЛИ — для установки, исключающее ИЛИ — для инвертирования битов регистра по маске.
Так, например, в сетевых интернет-технологиях операция И между значением IP-адреса и значением маски подсети используется для определения принадлежности данного адреса к подсети.
См. также
Примечания
- ↑ терминологические тонкости разъяснены в тексте
Устройство цифровых процессоров Архитектура Гарвардская • Фон Неймана • Битовые операции • Система команд • Кольца защиты • RISC • MISC • EPIC • 
Параллелизм Упреждающее выполнение • Конвейер • Суперскалярность • Подмена регистров • Мультипроцессор • Многопоточность Компоненты АЛУ • Математический сопроцессор • Корпус • Векторный процессор • Регистры • Кэш Питание Динамическое изменение частоты • Динамическое изменение напряжения Реализации Микропроцессор • Графический процессор • Физический процессор • DSP • Система на кристалле • Микроконтроллер • ПЛИС
Wikimedia Foundation. 2010.