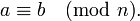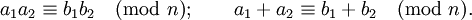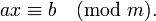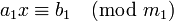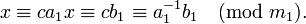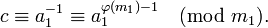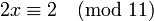- Кольцо вычетов
-
Сравнение по модулю натурального числа — отношение эквивалентности на множестве целых чисел, связанное с делимостью. Оно даёт возможность работать с системой чисел, более простой чем целые числа, в которой значения «зацикливаются» (повторяются) после достижения определенного значения.
В дискретной математике, для сравнений по модулю используется также термин модульная (или модулярная) арифметика.
Содержание
Определения
Говорят, что два целых числа a и b сравнимы по модулю натурального числа n, если при делении на n они дают одинаковые остатки.
Эквивалентные формулировки: a и b сравнимы по модулю n, если их разность a - b делится на n, или если a может быть представлено в виде a = b + kn, где k — некоторое целое число.
- Пример: 32 и −10 сравнимы по модулю 7, так как 32 = 7∙4 + 4, −10 = 7∙(-2) + 4.
Утверждение «a и b сравнимы по модулю n» записывается в виде:
Свойства
Отношение сравнения является отношением эквивалентности и обладает многими свойствами обычных равенств. Например, их можно складывать и перемножать: если
то
Сравнения, однако, нельзя, вообще говоря, делить друг на друга или на другие числа. Пример:
 , однако, сократив на 2, мы получаем ошибочное сравнение:
, однако, сократив на 2, мы получаем ошибочное сравнение: 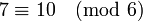 . Правила сокращения для сравнений следующие.
. Правила сокращения для сравнений следующие.- Можно делить обе части сравнения на число, взаимно простое с модулем: если
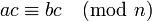 и НОД
и НОД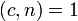 , то
, то 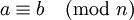 .
. - Можно одновременно разделить обе части сравнения и модуль на их общий делитель: если
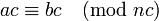 , то
, то 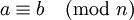 .
.
Нельзя также выполнять операции со сравнениями, если их модули не совпадают.
Другие свойства:
- Если
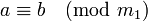 и
и 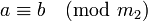 , то
, то 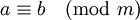 , где m = [m1,m2].
, где m = [m1,m2]. - Если
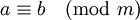 , то a, b сравнимы по любому модулю — делителю m.
, то a, b сравнимы по любому модулю — делителю m.
Классы вычетов
Множество всех чисел, сравнимых с a по модулю n называется классом вычетов a по модулю n, и обычно обозначается [a]n или
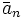 . Таким образом, сравнение
. Таким образом, сравнение 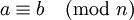 равносильно равенству классов вычетов [a]n = [b]n.
равносильно равенству классов вычетов [a]n = [b]n.Поскольку сравнение по модулю n является отношением эквивалентности на множестве целых чисел
 , то классы вычетов по модулю n представляют собой классы эквивалентности; их количество равно n. Множество всех классов вычетов по модулю n обозначается
, то классы вычетов по модулю n представляют собой классы эквивалентности; их количество равно n. Множество всех классов вычетов по модулю n обозначается 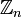 или
или 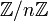 .
.Операции сложения и умножения на
 индуцируют соответствующие операции на множестве
индуцируют соответствующие операции на множестве 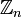 :
:- [a]n + [b]n = [a + b]n
![[a]_n\cdot [b]_n=[a\cdot b]_n](/pictures/wiki/files/99/cb8dd8e51b2583aa2bcaa03446e485c3.png)
Относительно этих операций множество
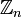 является конечным кольцом, а если n простое — конечным полем.
является конечным кольцом, а если n простое — конечным полем.Решение сравнений
Сравнения первой степени
В теории чисел, криптографии и других областях науки часто возникает задача отыскания решений сравнения первой степени вида:
Решение такого сравнения начинается с вычисления НОД(a, m)=d. При этом возможны 2 случая:
- Если b не кратно d, то у сравнения нет решений.
- Если b кратно d, то у сравнения существует единственное решение по модулю m / d, или, что то же самое, d решений по модулю m. В этом случае в результате сокращения исходного сравнения на d получается сравнение:
где a1 = a / d, b1 = b / d и m1 = m / d являются целыми числами, причем a1 и m1 взаимно просты. Поэтому число a1 можно обратить по модулю m1, то есть найти такое число c, что
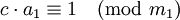 (другими словами,
(другими словами, 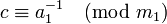 ). Теперь решение находится умножением полученного сравнения на c:
). Теперь решение находится умножением полученного сравнения на c:Практическое вычисление значения c можно осуществить разными способами: с помощью теоремы Эйлера, алгоритма Евклида, теории цепных дробей (см. алгоритм) и др. В частности, теорема Эйлера позволяет записать значение c в виде:
Пример: решим уравнение
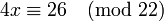 . Здесь d = 2, поэтому по модулю 22 сравнение имеет два решения. Заменим 26 на 4, сравнимое с ним по модулю 22, и затем сократим все 3 числа на 2:
. Здесь d = 2, поэтому по модулю 22 сравнение имеет два решения. Заменим 26 на 4, сравнимое с ним по модулю 22, и затем сократим все 3 числа на 2:Поскольку 2 взаимно просто с модулем 11, можно сократить левую и правую части на 2. В итоге получаем одно решение по модулю 11:
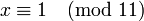 , эквивалентное двум решениям по модулю 22:
, эквивалентное двум решениям по модулю 22: 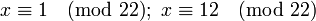 .
.Сравнения второй степени
Решение сравнений второй степени сводится к выяснению, является ли данное число квадратичным вычетом (с помощью квадратичного закона взаимности) и последующему вычислению квадратного корня по данному модулю.
История
В значительной степени теория делимости и вычетов была создана Эйлером. Сравнения по модулю впервые использовались Гауссом в его книге «Арифметические исследования», 1801 год. Он же предложил утвердившуюся в математике символику для сравнений.
Ссылки
- Вейль А., Основы теории чисел, М.:Мир, 1972.
- Виленкин Н. Я., Сравнения и классы вычетов, Квант, № 10, 1978.
- Виноградов И. М., Основы теории чисел, М.: ГИТТЛ, 1952.
Wikimedia Foundation. 2010.