- Гравитационный манёвр
-
 Гравитационный манёвр для ускорения объекта (гравитационная праща)
Гравитационный манёвр для ускорения объекта (гравитационная праща)
 Гравитационный манёвр для замедления объекта
Гравитационный манёвр для замедления объекта
Гравитационный манёвр — разгон, замедление или изменение направления полёта космического аппарата под действием гравитационных полей небесных тел. Используется для экономии топлива и достижения высоких скоростей при полётах автоматических межпланетных станций к дальним планетам Солнечной системы.
Рассмотрим траекторию космического аппарата, пролетающего вблизи какого-нибудь большого небесного тела, например, Юпитера. В начальном приближении мы можем пренебречь действием на космический аппарат гравитационных сил от других небесных тел.
В системе отсчёта, связанной с Юпитером, космический аппарат разгоняется, проходит точку с минимальным расстоянием до планеты, а потом замедляется. Общая траектория космического аппарата представляет собой гиперболу, причём скорости до и после манёвра совпадают.
Теперь посмотрим на ту же ситуацию в системе отсчёта, связанной с Солнцем. В этой системе отсчёта планета движется по орбите (в случае Юпитера, со скоростью более 13 км/с), поэтому скорость космического аппарата относительно Солнца может измениться. Таким образом, без затрат топлива можно изменить кинетическую энергию космического аппарата. Фактически, следует говорить о перераспределении кинетической энергии движения планеты и космического аппарата. Насколько возрастает (убывает) кинетическая энергия аппарата, настолько же падает (возрастает) кинетическая энергия движения планеты по её орбите. Поскольку масса искусственного космического аппарата исчезающе мала в сравнении с массой планеты (даже Луны), то изменения параметров орбиты планеты при этом оказываются исчезающе малыми, и ими можно полностью пренебречь. Например, если аппарат массой 1000 кг получает в поле тяготения Луны изменение скорости своего движения на 1 км/с, то скорость движения Луны по орбите вокруг Земли изменится лишь на несколько миллиардных долей ангстрема в секунду (то есть несколько миллиардных долей поперечника атома водорода). Другие тела Солнечной системы на движение Луны влияют на несколько порядков сильнее.
Наиболее выгодны гравитационные манёвры у планет-гигантов, но нередко используются манёвры у Венеры, Земли, Марса и даже Луны.
Максимально возможные приращения скорости, км/с:
Меркурий Венера Земля Луна Марс Юпитер Сатурн Уран Нептун Плутон 3,005 7,328 7,910 1,680 3,555 42,73 25,62 15,18 16,73 1,09 Российские историки космонавтики утверждают, что идея гравитационного манёвра была на практике осуществлена во время полёта космического аппарата «Е-2А» № 1 (с 1963 — Луна-3) — автоматической станции, которой впервые в мире удалось осуществить фотографирование обратной стороны Луны.
В 1974 году гравитационный манёвр использовал космический аппарат Маринер-10 — было произведено сближение с Венерой, после которого аппарат направился к Меркурию.
За счёт гравитационных манёвров скорость «Вояджера-1» (~17 км/с) в марте 2011 года была выше, чем текущая скорость «Новых горизонтов» (~15,9 км/с), хотя после старта с Земли скорость последнего была самой высокой для рукотворных объектов (16,21 км/сек[1]).
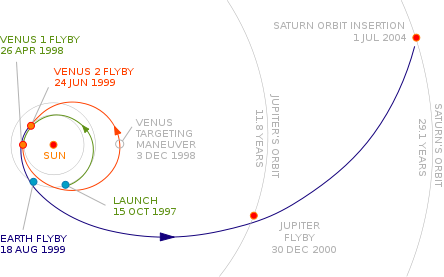
Сложную комбинацию гравитационных манёвров использовала «Кассини» — автоматическая межпланетная станция. Для разгона аппарат использовал гравитационное поле трёх планет — Венеры (дважды), Земли и Юпитера.
Также под гравитационным манёвром иногда понимается комбинированный способ ускорения космических аппаратов (Эффект Оберта). Суть данного способа заключается в том, что при выполнении гравитационного манёвра в «нижней» части траектории аппарат включает двигатель и сжигает топливо, получая дополнительное ускорение и переводя таким образом энергию топлива в кинетическую энергию корабля. Кроме того, за счёт этого при «подъёме» аппарата из гравитационного колодца планеты его кинетическая энергия не тратится на увеличение потенциальной энергии сожжённого топлива, что позволяет получить дополнительный выигрыш в скорости.
Художественное описание подобного манёвра можно встретить в фантастическом романе А. Кларка 2010: Одиссея 2.
Примечания
Ссылки
- «Ценный дар небесной механики»
- Руководство к MFD TransX V3.6+ (навигационные расчеты для космического симулятора «Орбитер», позволяет рассчитывать в том числе гравитационные манёвры)
- Гравитационные маневры АМС

Орбиты ТипыОсновные Box-орбита • Орбита захвата • Эллиптическая орбита / Высокая эллиптическая орбита • Орбита ухода • Орбита захоронения • Гиперболическая траектория • Наклонная орбита / Ненаклонная орбита • Оскулирующая орбита • Параболическая траектория • Опорная орбита (в т.ч. низкая) • Синхронная орбита • (Полусинхронная • Субсинхронная) • Стационарная орбита Геоцентрические Геосинхронная орбита • Геостационарная орбита • Солнечно-синхронная орбита • Низкая околоземная орбита • Средняя околоземная орбита • Высокая околоземная орбита • Молния-орбита • Околоэкваториальная орбита • Орбита Луны • Полярная орбита • Тундра-орбита • TLE Вокруг других
небесных тел и точекАреосинхронная орбита • Ареостационарная орбита • Гало-орбита • Орбита Лиссажу • Окололунная орбита • Гелиоцентрическая орбита • Солнечно-синхронная орбита ПараметрыКлассические  Наклонение ·
Наклонение ·  Долгота восходящего узла ·
Долгота восходящего узла ·  Эксцентриситет ·
Эксцентриситет ·  Аргумент перицентра ·
Аргумент перицентра ·  Большая полуось ·
Большая полуось ·  Средняя аномалия на эпоху
Средняя аномалия на эпохуДругие  Истинная аномалия ·
Истинная аномалия ·  Малая полуось ·
Малая полуось ·  Эксцентрическая аномалия ·
Эксцентрическая аномалия ·  Средняя долгота ·
Средняя долгота ·  Истинная долгота ·
Истинная долгота ·  Период обращенияОрбитальные манёврыБиэллиптическая переходная орбита · Запас характеристической скорости · Геопереходная орбита · Гравитационный манёвр · Гравитационный поворот · Орбита Гомана — Ветчинкина · Низкозатратная переходная траектория · Эффект Оберта · Изменение наклонения орбиты · Фазирование орбиты · Стыковка · Transposition, docking, and extraction · Манёвр уводаДругие темы астродинамикиСистема небесных координат · Экваториальная система координат · Эпоха · Эфемерида · Законы Кеплера · Гравитационная задача N тел · Точки Лагранжа · Пертурбация · Межпланетная транспортная сеть
Период обращенияОрбитальные манёврыБиэллиптическая переходная орбита · Запас характеристической скорости · Геопереходная орбита · Гравитационный манёвр · Гравитационный поворот · Орбита Гомана — Ветчинкина · Низкозатратная переходная траектория · Эффект Оберта · Изменение наклонения орбиты · Фазирование орбиты · Стыковка · Transposition, docking, and extraction · Манёвр уводаДругие темы астродинамикиСистема небесных координат · Экваториальная система координат · Эпоха · Эфемерида · Законы Кеплера · Гравитационная задача N тел · Точки Лагранжа · Пертурбация · Межпланетная транспортная сеть
Уравнение орбиты · Апоцентр и перицентр · Орбитальная скорость · Орбитальные векторы состояния · Специальная орбитальная энергия · Специальный относительный вращательный момент · Прямое движение · Ретроградное движение · Трасса орбитыКатегории:- Гравитация
- Астродинамика
- Нерешённые проблемы современной физики
Wikimedia Foundation. 2010.