Эффект Козаи

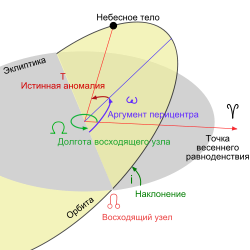
В небесной механике механизмом, эффектом или резонансом Козаи (в России иногда указывается как механизм Лидова^[1]-Козаи) называется периодическое изменение соотношения эксцентриситета и наклонения орбиты, учитывая воздействие массивного тела или тел. Таким образом, либрации (колебания вокруг постоянных значений) происходит в аргументе перицентра.

Этот эффект был описан в 1962 японским астрономом Ёсихидэ Козаи (en:Yoshihide Kozai) (более правильно его имя звучит как Ёсихидэ Кодзай (яп. 古在 由秀 Кодзай Ёсихидэ^?), когда он анализировал орбиты астероидов^[2]. Как показали дальнейшие исследования резонанс Козаи является важным фактором, формирующим орбиты нерегулярных спутников планет, Транснептуновых объектов, а также внесолнечных планет и кратных звездных систем^[3].

Резонанс Козаи

Схема аргумента перицентра

Для небесного тела с эксцентриситетом $e\,\!$ и наклонением $i\,\!$, которое вращается вокруг большего тела, сохраняется следующее постоянное соотношение:

$\sqrt{(1-e^2)} \cos i$

Глядя на это соотношение, можно сказать, что эксцентриситет может быть «обменян» на наклонение и наоборот, и это периодическое колебание может привести к резонансу между двумя небесными телами. Таким образом, почти круговые, чрезвычайно наклонные орбиты могут получить очень большой эксцентриситет в обмен на меньшее наклонение. Так, например, увеличивающийся эксцентриситет, при постоянной большой полуоси уменьшает расстояние между объектами в перигелии, и этот механизм может заставить кометы становиться околосолнечными.

Как правило, для объектов на орбитах с низким наклонением подобные колебания приводят к прецессии аргумента перицентра. Начинаясь с некоторой значения угла, прецессия переходит в либрацию в диапазоне приблизительно 90° или 270°, и перицентр (точка максимального сближения) будет колебаться вокруг этих значений. Минимальный угол наклонения называется углом Козаи и равен:

$\arccos\left(\sqrt\frac{3}{5}\right) \approx 39.2^{o}$

Для ретроградных спутников он равен 140,8°.

Физически эффект связан с передачей момента импульса и сохранением его общего количества в связанной системе (см. также интеграл Якоби).

Применение

Механизм Козаи является причиной того, что небесное тело располагается в перицентре, когда оно находится на самом большом расстоянии от экваториальной плоскости. Этот эффект — часть причины того, что Плутон защищен от столкновений с Нептуном^[4].

Резонанс Козаи также устанавливает ограничения для орбит, возможных в пределах системы, например:

• для регулярных спутников планет: если орбита спутника планеты будет сильно наклонена к орбите планеты, то эксцентриситет лунной орбиты будет увеличиваться до тех пор пока луна не будет разрушена приливными силами при очередном сближении^[1].
• для нерегулярных спутников: растущий эксцентриситет приведет к столкновению с другим спутником (планетой), или, при их отсутствии, рост апоцентра может выбросить спутник из сферы Хилла.

Внешние ссылки

• Механизм Козаи  (англ.)

Примечания

1. ↑ ^{1 2} М. Л. ЛИДОВ — УЧЕНЫЙ И ЧЕЛОВЕК
2. ↑ Y. Kozai, Secular perturbations of asteroids with high inclination and eccentricity. Astronomical Journal (11/1962). Архивировано из первоисточника 17 апреля 2012. (англ.)
3. ↑ Innanen et al. Linqing Wen. О распределении эксцентриситетов сливающихся двойных черных дыр в шаровых скоплениях порождаемом эффектом Козаи (On the Eccentricity Distribution of Coalescing Black Hole Binaries Driven by the Kozai Mechanism in Globular Clusters). arXiv.org (22 Nov 2002). (англ.)
4. ↑ Innanen et al. The Kozai Mechanism and the stability of planetary orbits in binary star systems. Astronomical Journal (05/1997). Архивировано из первоисточника 17 апреля 2012. (англ.)