Гомановская траектория

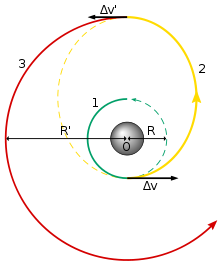
Гомановская траектория перехода (желтый) с низкой круговой орбиты (зеленый) на более высокую круговую орбиту (красный). Δv и Δv' — первое и второе включения двигателя на разгон.

Го́мановская траекто́рия (орбита Гомана — Ветчинкина) — в небесной механике эллиптическая орбита, используемая для перехода между двумя другими орбитами, обычно находящимися в одной плоскости. В простейшем случае, она пересекает эти две орбиты в апоцентре и перицентре^[1]. Орбитальный маневр для перехода включает в себя 2 импульса работы двигателя на разгон — для входа на гомановскую траекторию и для схода с неё. Названа в честь немецкого учёного Вальтера Гомана, в 1925 году описавшего её в своей книге^[2]. На Гомана оказал большое влияние писатель-фантаст Курд Лассвиц своей книгой 1897 года «Две планеты». Эту же траекторию разработали независимо советские учёные Владимир Ветчинкин и Фридрих Цандер^[3].

Гомановская траектория теоретически рассчитывается для двух импульсных (условно мгновенных) приращений скорости. Однако, поскольку время работы двигателя (нужное для набора соответствующего приращения скорости) отличается от нуля, то импульс должен быть как можно более коротким; соответственно, требуется применять двигатели с большой тягой. Если же космический аппарат оснащен только двигателями малой тяги, то выполнение перехода по гомановской траектории потребует нескольких включений двигателя, что резко снизит энергетическую выгоду перехода по такой траектории (нужное приращение скорости составит до 141 % от двухимпульсного маневра).

Для гомановской траектории угловая дальность (угол между лучами, проведёнными из точки O в начальную и конечную точки траектории) равна 180 градусов. Если она меньше 180 градусов, траектория называется траекторией первого полувитка, или типа 1, а если больше — траекторией второго полувитка, или типа 2.

Примечания

1. ↑ Л. В. Ксанфомалити Ценный дар небесной механики. Вселенная и мы. Архивировано из первоисточника 25 августа 2012. Проверено 11 августа 2011.
2. ↑ Walter Hohmann Die Erreichbarkeit der Himmelskörper. — Verlag Oldenbourg in München, 1925. — ISBN 3-486-23106-5
3. ↑ Салахутдинов Г. М. Фридрих Артурович Цандер (К 100-летию со дня рождения). — М.: Знание, 1987. — 64 с, ил. — (Новое в жизни, науке, технике. Сер. «Космонавтика, астрономия»; № 3).