Целые алгебраические числа
- Целые алгебраические числа
-
Целыми алгебраическими числами называются комплексные (и в частности вещественные) корни многочленов с целыми коэффициентами и со старшим коэффициентом, равным единице.
По отношению к сложению и умножению комплексных чисел, целые алгебраические числа образуют кольцо Ω. Очевидно, Ω является подкольцом поля алгебраических чисел и содержит все обычные целые числа.
Пусть u — некоторое комплексное число. Рассмотрим кольцо ![\mathbb{Z}[u]](/pictures/wiki/files/99/c7383c92cedf1d588bf34450d4eaf76e.png) , порождённое добавлением u к кольцу обычных целых чисел
, порождённое добавлением u к кольцу обычных целых чисел  . Оно образовано всевозможными значениями f(u), где f(z) — многочлен с целыми коэффициентами. Тогда имеет место следующий критерий: число u является целым алгебраическим числом тогда и только тогда, когда
. Оно образовано всевозможными значениями f(u), где f(z) — многочлен с целыми коэффициентами. Тогда имеет место следующий критерий: число u является целым алгебраическим числом тогда и только тогда, когда ![\mathbb{Z}[u]](/pictures/wiki/files/99/c7383c92cedf1d588bf34450d4eaf76e.png) — конечнопорождённая абелева группа.
— конечнопорождённая абелева группа.
Примеры целых алгебраических чисел
Свойства
- Все рациональные числа, входящие в Ω, являются на деле целыми числами. Другими словами, ни одна несократимая дробь m / n со знаменателем, большим единицы, целым алгебраическим числом быть не может.
- Для каждого алгебраического числа u существует натуральное число n такое, что nu — целое алгебраическое число.
- Корень любой степени из целого алгебраического числа тоже является целым алгебраическим числом.
История
Теорию целых алгебраических чисел создали в XIX веке Гаусс, Якоби, Дедекинд, Куммер и другие. Интерес к ней был, в частности, вызван тем, что исторически эта структура оказалась первой в математике, где было обнаружено неоднозначное разложение на простые множители. Классические примеры построил Куммер; скажем, в подкольце целых алгебраических чисел вида 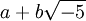 имеют место 2 разложения:
имеют место 2 разложения:
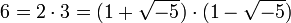 ,
,
причём в обоих случаях все множители — простые, то есть неразложимы в этом подкольце.
Исследование этой проблемы привело к открытию важных понятий идеала и простого идеала, в структуре которых разложение на простые множители стало возможным определить однозначно.
Литература
- К. Айерлэнд, М. Роузен. Классическое введение в современную теорию чисел. Перевод с английского С. П. Демушкина под редакцией А. Н. Паршина. М.: Мир, 1987, глава 6.
- Боревич З. И., Шафаревич И. P. Теория чисел. М., 1964.
- Ван дер Варден Б. Л. Алгебра. М.: Мир, 1975, глава 17: Целые алгебраические элементы.
- Гекке Э. Лекции по теории алгебраических чисел, пер. с нем., М. — Л., 1940.
- Гельфонд А. О. Трансцендентные и алгебраические числа, М., 1952.
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Целые алгебраические числа" в других словарях:
Целые алгебраические числа — числа, являющиеся корнями уравнений вида xn + a1xn 1 +... + an = 0, где a1,..., an целые рациональные числа. Например, x1 = 2 + Ц. а. ч., так как x12 4x1 + 1 = 0. Теория Ц. а. ч. возникла в 30 40 x гг. 19 в. в связи с исследованиями К.… … Большая советская энциклопедия
Целые комплексные числа — гауссовы числа, числа вида а + bi, где а и b целые числа (например, 4 7i). Геометрически изображаются точками комплексной плоскости, имеющими целочисленные координаты. Ц. к. ч. введены К. Гауссом в 1831 в связи с исследованиями по теории… … Большая советская энциклопедия
Целые числа — Множество целых чисел определяется как замыкание множества натуральных чисел относительно арифметических операций сложения (+) и вычитания ( ). Таким образом, сумма, разность и произведение двух целых чисел есть снова целые числа. Оно состоит из… … Википедия
Целые кватернионы — Кватернионы (англ. quaternion) это система гиперкомплексных чисел, предложенная У. Р. Гамильтоном в 1843 году. Умножение кватернионов некоммутативно; они образуют тело, которое обычно обозначается . Кватернионы очень удобны для описания… … Википедия
Числа Кэли — Алгебра Кэли определённый тип гиперкомплексных чисел, 8 мерная алгебра над полем вещественных чисел. Обычно обозначается , поскольку её элементы (числа Кэли) называются иногда октонионами или октавами. Число Кэли это линейная комбинация… … Википедия
Гауссовы целые числа — (гауссовы числа, целые комплексные числа) это комплексные числа, у которых как вещественная, так и мнимая часть целые числа. Введены Гауссом в 1825 году. Содержание 1 Определение и операции 2 Теория делимости … Википедия
Конструктивные способы определения вещественного числа — При конструктивном подходе к определению вещественного числа вещественные числа строят, исходя из рациональных, которые считают заданными. Во всех трёх нижеизложенных способах за основу берутся рациональные числа и конструируются новые объекты,… … Википедия
Иррациональные числа — Иррациональное число это вещественное число, которое не является рациональным, то есть которое не может быть представленным в виде дроби , где m целое число, n натуральное число. О существовании иррациональных чисел, точнее отрезков,… … Википедия
Дуальные числа — или (гипер)комплексные числа параболического типа гиперкомплексные числа вида , где и вещественные числа, и . Любое дуальное число однозначно определяется такой парой чисел и . Множество всех дуальных чисел образует двумерную коммутативную … Википедия
Простые числа — Простое число это натуральное число, которое имеет ровно 2 различных делителя (только 1 и самого себя). Все остальные числа, не равные единице, называются составными. Таким образом, все натуральные числа, за исключением единицы, разбиваются на… … Википедия
![\mathbb{Z}[u]](/pictures/wiki/files/99/c7383c92cedf1d588bf34450d4eaf76e.png) , порождённое добавлением u к кольцу обычных целых чисел
, порождённое добавлением u к кольцу обычных целых чисел  . Оно образовано всевозможными значениями f(u), где f(z) — многочлен с целыми коэффициентами. Тогда имеет место следующий критерий: число u является целым алгебраическим числом тогда и только тогда, когда
. Оно образовано всевозможными значениями f(u), где f(z) — многочлен с целыми коэффициентами. Тогда имеет место следующий критерий: число u является целым алгебраическим числом тогда и только тогда, когда ![\mathbb{Z}[u]](/pictures/wiki/files/99/c7383c92cedf1d588bf34450d4eaf76e.png) — конечнопорождённая абелева группа.
— конечнопорождённая абелева группа.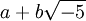 имеют место 2 разложения:
имеют место 2 разложения: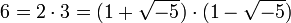 ,
,