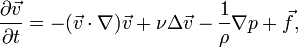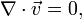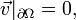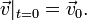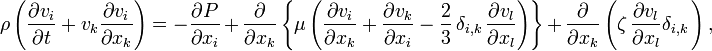- Уравнение Навье — Стокса
-
Механика сплошных сред 
Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоэластичность Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнения Навье — Стокса · Уравнение диффузии · Закон Гука Известные учёные Ньютон · Гук
Бернулли · Эйлер · Коши · Стокс · НавьеУравне́ния Навье́ — Сто́кса — система дифференциальных уравнений в частных производных, описывающая движение вязкой ньютоновской жидкости. Уравнения Навье — Стокса являются одними из важнейших в гидродинамике и применяются в математическом моделировании многих природных явлений и технических задач. Названы по имени французского физика Луи Навье и британского математика Джорджа Стокса.
Система состоит из двух уравнений:
- уравнения движения,
- уравнения неразрывности.
В векторном виде для несжимаемой жидкости они записываются следующим образом:
где
 — оператор Гамильтона, Δ — оператор Лапласа, t — время, ν — коэффициент кинематической вязкости, ρ — плотность, p — давление,
— оператор Гамильтона, Δ — оператор Лапласа, t — время, ν — коэффициент кинематической вязкости, ρ — плотность, p — давление, 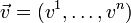 — векторное поле скоростей,
— векторное поле скоростей, 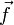 — векторное поле массовых сил. Неизвестные p и
— векторное поле массовых сил. Неизвестные p и 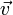 являются функциями времени t и координаты
являются функциями времени t и координаты 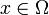 , где
, где 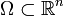 , n = 2,3 — плоская или трехмерная область, в которой движется жидкость. Обычно в систему уравнений Навье-Стокса добавляют краевые и начальные условия, например
, n = 2,3 — плоская или трехмерная область, в которой движется жидкость. Обычно в систему уравнений Навье-Стокса добавляют краевые и начальные условия, напримерИногда в систему уравнений Навье — Стокса дополнительно включают уравнение теплопроводности и уравнение состояния.
При учёте сжимаемости уравнение Навье — Стокса принимает следующий вид:
где μ — коэффициент динамической вязкости, ζ — «вторая вязкость».
Содержание
Анализ и решение уравнений
Задачи тысячелетия Равенство классов P и NP Гипотеза Ходжа Гипотеза Пуанкаре Гипотеза Римана Квантовая теория Янга — Миллса Существование и гладкость решений уравнений Навье — Стокса Гипотеза Берча и Свиннертона — Дайера В анализе решений уравнений заключается суть одной из открытых проблем, за решение которых Математический институт Клэя назначил премию в 1 млн долларов США. Необходимо доказать или опровергнуть существование глобального гладкого решения задачи Коши для трехмерных уравнений Навье — Стокса. Нахождение общего аналитического решения системы Навье — Стокса для пространственного или плоского потока осложняется тем, что оно нелинейное и сильно зависит от начальных и граничных условий.
Также ряд коммерческих фирм, например
До сих пор решения этих уравнений найдены лишь в некоторых частных случаях. В настоящее время существует несколько ситуаций (обусловленных простой геометрией), которые решены в аналитическом виде. В остальных случаях используется численное моделирование.
Некоторые точные решения:
- Стационарные течения в простых каналах (течение Пуазейля, течение Тейлора-Куэтта и пр.)
- Солитоны и нелинейные волны. Обычный солитон может являться решением системы при очень сложных граничных условиях. Впервые он наблюдался экспериментально в канале инженером Скотом Расселом.
- Решение, которое существует конечное время (так называемые режимы с обострением, blow-up). Капнув каплю на поверхность воды, можно наблюдать всплеск, который существует конечное время, как и кольцевой вихрь ядерного взрыва. Гипотеза об этом выдвинута Jean Leray в 1933 г. Он предположил, что в жидкости турбулентность (хаос) образуется благодаря образованию точек или вихревой нити, на которой некоторая компонента скорости становится бесконечной.
- Звуковые колебания. При малой амплитуде волн они также становятся решением. Нелинейные члены уравнения можно отбросить, так как они не влияют на решение. Решением являются гармонические функции синуса или косинуса, то есть звуковые колебания, которые мы слышим.
Основные свойства системы Навье — Стокса
- При превышении числа Рейнольдса выше некоторого критического числа, аналитическое точное решение для пространственного или плоского потока имеют хаотический вид (так называемая турбулентность). В частном случае, оно связано с теорией Фейгенбаума или другими сценариями перехода к хаосу. При уменьшении числа Рейнольдса ниже критического, решение опять принимает не хаотический вид.
- Исключительная чувствительность к изменению коэффициентов уравнения при турбулентном режиме: при изменении числа Re на 0,05 % решения совершенно отличаются друг от друга.
- Существует мнение (Бударин В.А. Анализ скрытых свойств системы Навье-Стокса//Тез. докл. 6 Минск. межд.форум, ИТМО.— 2008 — т.1.— С.75-76), что данное уравнение является приближенным. Это обосновывается использованием при выводе уравнения Навье-Стокса линейного уравнения для нахождения давления p, как функции его нелинейных компонентов. Такая позиция обьясняет существование различных значений числа Рейнольдса (для различных частных задач), в пределах которого линейный закон осреднения корректен.
Применение
Одним из применений системы уравнений Навье — Стокса является описание течений в мантии Земли («проблема динамо»).
Вариации уравнения Навье — Стокса используются для описания движения воздушных масс атмосферы, в частности, при формировании прогноза погоды. Для описания реальных течений в различных технических устройствах приемлемую точность численного решения можно получить только при такой расчётной сетке, ячейки которой меньше самого мелкого вихря. Это требует очень больших затрат расчётного времени на современных компьютерах. Поэтому были созданы различные модели турбулентности, упрощающие расчёт реальных потоков.
См. также
- Открытые математические проблемы
- Уравнение Эйлера (для невязкой жидкости)
Литература
- Темам Р. Уравнения Навье-Стокса. Теория и численный анализ. — 2-е изд. — М.: Мир, 1981. — 408 с.
- Ландау, Л. Д., Лифшиц, Е. М. Гидродинамика. — Издание 4-е, стереотипное.. — М.: Наука, 1988. — 736 с. — («Теоретическая физика», том VI).
- Кутепов А. М., Стерман Л. С., Стюшин Н. Г. Гидродинамика и теплообмен при парообразовании. — 3-е изд., испр.. — М.: Высшая школа, 1986. — 448 с.
- Кутепов А. М., Полянин А. Д., Запрянов З. Д., Вязьмин А. В., Казенин Д. А. Химическая гидродинамика. — М.: Квантум, 1996. — 336 с. — 1500 экз.
Wikimedia Foundation. 2010.