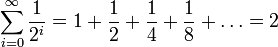Ряд (математич.) — Ряд, бесконечная сумма, например вида u1 + u2 + u3 +... + un +... или, короче, . (1) Одним из простейших примеров Р., встречающихся уже в элементарной математике, является сумма бесконечно убывающей геометрической прогрессии 1 + q + q 2 +... + q… … Большая советская энциклопедия
РЯД — б е с к о н е ч н а я с у м м а, последовательность элементов (наз. ч л е н а м и д а н н о г о р я д а) нек рого линейного топологич. пространства и определенное бесконечное множество их конечных сумм (наз. ч а с т и ч н ы м и с у м м а м и р я… … Математическая энциклопедия
ОРТОГОНАЛЬНЫЙ РЯД — ряд вида где ортонормированная система функций (онс) относительно меры : Начиная с 18 в. при изучении различных вопросов математики, астрономии, механики и физики (движение планет, колебание струн, мембран и др.) в исследованиях Л. Эйлера (L.… … Математическая энциклопедия
ТРИГОНОМЕТРИЧЕСКИЙ РЯД — ряд по косинусам и синусам кратных дуг, т. е. ряд вида или в комплексной форме где ak, bk или, соответственно, ck наз. коэффициентами Т. р. Впервые Т. р. встречаются у Л. Эйлера (L. Euler, 1744). Он получил разложения В сер. 18 в. в связи с… … Математическая энциклопедия
РАСХОДЯЩИЙСЯ РЯД — ряд, у к рого последовательность частичных сумм не имеет конечного предела. Напр., ряды расходятся. Р. р. стали появляться в работах математиков 17 18 вв. Л. Эйлер (L. Euler) первым пришел к выводу, что нужно ставить вопрос, не чему равна сумма,… … Математическая энциклопедия
ЛАКУНАРНЫЙ РЯД — ряд по лакунарной системе функций. Примерами служат лакунарные тригонометрич. ряды, лакунарные степенные ряды, ряды Радемахера, ряды независимых функций с нулевыми математич. ожиданиями, ряды Дирихле с показателями, независимыми над полем… … Математическая энциклопедия
Спектр (математич.) — Спектр колебаний, совокупность простых гармонических колебаний, на которые может быть разложено данное сложное колебательное движение. Математически такое движение может быть представлено в виде периодической, но негармонической функции f(t) с… … Большая советская энциклопедия
КОНСТРУКТИВНАЯ МАТЕМАТИКА — конструктивное направление в математике, математика, строящаяся в соответствии с тем или иным конструктивным математич. мировоззрением, обыкновенно стремящимся связывать утверждения о существовании математнч. объектов с возможностью их построения … Математическая энциклопедия
Киприянов, Василий Анофриевич (Онуфриевич) — (г. рожд. неизв. ум. 1723, по нек рым источникам 1728) рус. печатник и издатель, сподвижник Петра I. Выходец из среды посадских людей Кадашевской слободы в Москве. В 1701 03 принимал участие в издании "Арифметики" Л. Магницкого. В 1705… … Большая биографическая энциклопедия
Оттоновское возрождение — краткий период (конец X в.) подъема культурной жизни в Германии при императорах Саксонской династии Отгонах. При дворе Оттона I возродилась Академия, где собирались просвещенные люди. Здесь развивалась литературная деятельность, переписывались… … Средневековый мир в терминах, именах и названиях
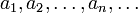 — последовательность чисел. Число
— последовательность чисел. Число 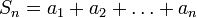 называется n-ой частичной суммой ряда
называется n-ой частичной суммой ряда 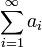 .
.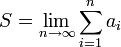 , то в этом случае пишут
, то в этом случае пишут 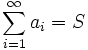 .
.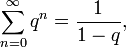 где | q | < 1, — сумма геометрической прогрессии, в частности
где | q | < 1, — сумма геометрической прогрессии, в частности
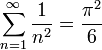 .
.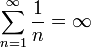 - гармонический ряд расходится.
- гармонический ряд расходится.