Поля Галуа

Толкование

Поля Галуа

Конечное поле или поле Галуа — поле, состоящее из конечного числа элементов.

Конечное поле обычно обозначается 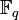$\mathbb{F}_q$ или $GF(q)$ , где $q$ — число элементов поля.

Простейшим примером конечного поля является 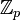$\mathbb{Z}_p$ — кольцо вычетов по модулю простого числа.

Содержание

1 Свойства конечных полей
2 Примеры конечных полей
3 Построение конечных полей
- 3.1 Пример построения поля GF(9)
  - 3.1.1 Таблица сложения в GF(9)
  - 3.1.2 Таблица умножения в GF(9)
4 Литература
5 См. также

Свойства конечных полей

Характеристика конечного поля является простым числом.
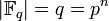Число элементов любого конечного поля есть его характеристика в натуральной степени: $|\mathbb{F}_q|=q=p^n$ .
Для каждого простого числа $p$ и натурального $n$ существует конечное поле из $q = p n$ элементов, единственное с точностью до изоморфизма. Это поле изоморфно полю разложения многочлена $x^q-x\in\mathbb{F}_p[x]$ .
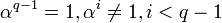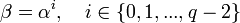В каждом поле существует по крайней мере один примитивный элемент $α$ , то есть такой, что $\alpha^{q-1}=1, \alpha^i \neq 1, i&lt; q-1$ . Любой ненулевой элемент $β$ является некоторой степенью примитивного элемента: $\beta = \alpha^i,\quad i \in \{0,1,...,q-2\}$ .
Мультипликативная группа 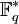$\mathbb{F}^*_q$ конечного поля 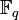$\mathbb{F}_q$ является циклической группой порядка $q - 1$ . Поэтому, в частности, в конечном поле всегда существует примитивный элемент $α$ , порядок которого равен $q - 1$ , то есть $α q - 1 = 1$ и 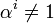$\alpha^i \neq 1$ для $0 < i < q - 1$ .
Поле 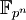$\mathbb{F}_{p^n}$ содержит в себе в качестве подполя 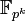$\mathbb{F}_{p^k}$ тогда и только тогда, когда $k$ является делителем $n$ .

Примеры конечных полей

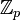$\mathbb{Z}_p$ , где $p$ — простое: 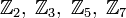$\mathbb{Z}_2,\;\mathbb{Z}_3,\;\mathbb{Z}_5,\;\mathbb{Z}_7$ и так далее.
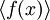$\mathrm{GF}(p^n)=\mathbb{Z}_p[x]/\langle f(x)\rangle$ , где $\langle f(x)\rangle$ — главный идеал кольца $\mathbb{Z}_p[x]$ , порожденный неприводимым многочленом $f(x)\in\mathbb{Z}_p[x]$ степени $n$ .

Построение конечных полей

Существует два варианта построения, в зависимости от количества элементов поля, которое необходимо построить:

Поле содержит $p$ элементов, где $p$ — простое.

Кольцо 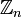$\mathbb{Z}_n$ вычетов по модулю

n

в случае простого

n = p

не имеет делителей нуля и является полем.

Элементы 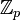$\mathbb{Z}_p$ — числа 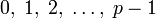$0,\;1,\;2,\;\ldots,\;p-1$ . Операции проводятся как с обычными целыми числами с приведением по модулю

p

Поле содержит $q = p n$ элементов, где $p$ — простое, $n$ — натуральное.

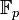Кольцо $\mathbb{K}=\mathbb{F}_p[x]/\langle f(x)\rangle$ является полем тогда и только тогда, когда многочлен

f (x)

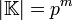неприводим над полем $\mathbb{F}_p$ . При этом $|\mathbb{K}|=p^m$ , где

m = deg(f)

. Таким образом, для построения поля из

q = p n

элементов достаточно отыскать многочлен степени

n

, неприводимый над полем 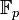$\mathbb{F}_p$ , и определить $\mathbb{K}$ как указано выше.

Элементами поля $\mathbb{K}$ являются все многочлены степени меньшей

n

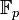с коэффициентами из $\mathbb{F}_p$ . Операции (сложение и умножение) проводятся по модулю многочлена

f (x)

, то есть результат соответствующей операции — это остаток от деления на

f (x)

с приведением коэффициентов по модулю

p

Пример построения поля GF(9)

Пусть надо построить поле $GF(9) = GF(3 2)$ . Для этого необходимо найти многочлен степени 2, неприводимый в 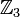$\mathbb{Z}_3$ . Такими многочленами являются

x 2 + 1

x 2 + x + 2

x 2 + 2 x + 2

2 x 2 + 2

2 x 2 + x + 1

2 x 2 + 2 x + 1

Возьмём, например, $x 2 + 1$ , тогда искомое поле есть $\mathrm{GF}(9)=\mathbb{Z}_3[x]/\langle x^2+1\rangle$ . Если вместо $x 2 + 1$ взять другой многочлен, то получится новое поле, изоморфное старому.

Таблица сложения в GF(9)

$\mathrm{GF}(9)=\mathbb{Z}_3[x]/\langle x^2+1\rangle$

+	0	1	2	$x$	$x + 1$	$x + 2$	$2 x$	$2 x + 1$	$2 x + 2$
0	0	1	2	$x$	$x + 1$	$x + 2$	$2 x$	$2 x + 1$	$2 x + 2$
1	1	2	0	$x + 1$	$x + 2$	$x$	$2 x + 1$	$2 x + 2$	$2 x$
2	2	0	1	$x + 2$	$x$	$x + 1$	$2 x + 2$	$2 x$	$2 x + 1$
$x$	$x$	$x + 1$	$x + 2$	$2 x$	$2 x + 1$	$2 x + 2$	0	1	2
$x + 1$	$x + 1$	$x + 2$	$x$	$2 x + 1$	$2 x + 2$	$2 x$	1	2	0
$x + 2$	$x + 2$	$x$	$x + 1$	$2 x + 2$	$2 x$	$2 x + 1$	2	0	1
$2 x$	$2 x$	$2 x + 1$	$2 x + 2$	0	1	2	$x$	$x + 1$	$x + 2$
$2 x + 1$	$2 x + 1$	$2 x + 2$	$2 x$	1	2	0	$x + 1$	$x + 2$	$x$
$2 x + 2$	$2 x + 2$	$2 x$	$2 x + 1$	2	0	1	$x + 2$	$x$	$x + 1$

Таблица умножения в GF(9)

$\mathrm{GF}(9)=\mathbb{Z}_3[x]/\langle x^2+1\rangle$

×	1	2	$x$	$x + 1$	$x + 2$	$2 x$	$2 x + 1$	$2 x + 2$
0	0	0	0	0	0	0	0	0
1	1	2	$x$	$x + 1$	$x + 2$	$2 x$	$2 x + 1$	$2 x + 2$
2	2	1	$2 x$	$2 x + 2$	$2 x + 1$	$x$	$x + 2$	$x + 1$
$x$	$x$	$2 x$	2	$x + 2$	$2 x + 2$	1	$x + 1$	$2 x + 1$
$x + 1$	$x + 1$	$2 x + 2$	$x + 2$	$2 x$	1	$2 x + 1$	2	$x$
$x + 2$	$x + 2$	$2 x + 1$	$2 x + 2$	1	$x$	$x + 1$	$2 x$	2
$2 x$	$2 x$	$x$	1	$2 x + 1$	$x + 1$	2	$2 x + 2$	$x + 2$
$2 x + 1$	$2 x + 1$	$x + 2$	$x + 1$	2	$2 x$	$2 x + 2$	$x$	1
$2 x + 2$	$2 x + 2$	$x + 1$	$2 x + 1$	$x$	2	$x + 2$	1	$2 x$

Литература

Винберг Э.Б. Курс алгебры. — 3-е изд.. — М.: Факториал Пресс, 2002. — 544 с. — 3000 экз. — ISBN 5-88688-060-7

См. также

Wikimedia Foundation. 2010.

Игры ⚽ Нужна курсовая?

Полезное

Смотреть что такое "Поля Галуа" в других словарях:

Галуа — Галуа, Эварист Портрет Эвариста Галуа. Сделан с натуры, когда ему было пятнадцать лет, нарисован карандашом Эварист Галуа (фр. Évariste Galois; 26 октября 1811, Бур ля Рен, О де Сен, Франция 31 мая … Википедия
ГАЛУА РАСШИРЕНИЕ — поля нормальное и се парабельное расширение поля. Изучение группы автоморфизмов таких расширений относится к Галуа теории … Математическая энциклопедия
ГАЛУА ТЕОРИЯ — в наиболее общем смысле теория, изучающая те или иные математич. объекты на основе их групп автоморфизмов. Так, напр., возможны Г. т. полей, колец, топологич. пространств и т. п. В более узком смысле под Г. т. понимается Г. т. полей. Возникла эта … Математическая энциклопедия
ГАЛУА КОГОМОЛОГИИ — когомологии Галуа группы. Если М абелева группа и группа Галуа расширения , действующая на М, то когомологии Галуа есть группы когомологии определяемые комплексом состоит из всех отображений , a d кограничный оператор (см. Когомологии групп).… … Математическая энциклопедия
ГАЛУА ГРУППА — группа автоморфизмов Галуа расширения L поля k, т. е. группа, состоящая из всех автоморфизмов поля L, оставляющих все элементы подполя k неподвижными. Г. г. обозначается или . Поле инвариантов совпадает с полем k. Если L поле разложения… … Математическая энциклопедия
ГАЛУА ТЕОРИИ ОБРАТНАЯ ЗАДАЧА — задача построения конечного нормального расширения для данного поля kс заданной Галуа группой (см. Галуа теория), а также выяснения условий, обеспечивающих существование или отсутствие такого расширения над полем k. Если kесть поле рациональных… … Математическая энциклопедия
ГАЛУА ПОЛЕ — конечное поле, поле, число элементов к рого конечно. Г. п. впервые рассматривалось Э. Галуа (Е. Galois, см. [1], с. 35 47). Число элементов любого Г. п. есть степень нек рого натурального простого числа , являющегося характеристикой этого поля.… … Математическая энциклопедия
Галуа, Эварист — Эварист Галуа Évariste Galois Портрет Эвариста Галуа. Сделан с натуры, когда ему было пятнадцать лет, нарисован карандашом … Википедия
ГАЛУА ТОПОЛОГИЧЕСКАЯ ГРУППА — группа Галуа, снабженная топологией Крулля; базис фильтра этой топологии состоит из нормальных делителей конечного индекса. Если конечное расширение Галуа, то топология его группы Галуа дискретна. Если поле L объединение конечных расширений Галуа … Математическая энциклопедия
ГАЛУА ТЕОРИЯ КОЛЕЦ — обобщение результатов теории Галуа полей на случай ассоциативных колец с единицей. Пусть А ассоциативное кольцо с единицей, Н некоторая подгруппа группы всех автоморфизмов кольца А, N подгруппа группы Н, . Тогда подкольцо кольца А. Пусть… … Математическая энциклопедия

Словари и энциклопедии на Академике

Поля Галуа

Содержание

Свойства конечных полей

Примеры конечных полей

Построение конечных полей

Пример построения поля GF(9)

Таблица сложения в GF(9)

Таблица умножения в GF(9)

Литература

См. также

Полезное

Смотреть что такое "Поля Галуа" в других словарях:

Поделиться ссылкой на выделенное

Словари и энциклопедии на Академике

Википедия

Поля Галуа

Содержание

Свойства конечных полей

Примеры конечных полей

Построение конечных полей

Пример построения поля GF(9)

Таблица сложения в GF(9)

Таблица умножения в GF(9)

Литература

См. также

Полезное

Смотреть что такое "Поля Галуа" в других словарях:

Поделиться ссылкой на выделенное

Прямая ссылка: