ГАЛУА ГРУППА

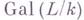- группа автоморфизмов Галуа расширения L поля k, т. е. группа, состоящая из всех автоморфизмов поля L, оставляющих все элементы подполя k неподвижными. Г. г. обозначается или . Поле инвариантов совпадает с полем k. Если L - поле разложения многочлена f над полем k, то Г. г. наз. также группой Галуа многочлена f. Эти группы играют важную роль в теории Галуа алгебраич. уравнений. Вычисление Г. г. для расширений полей алгебраич. чисел является одной из основных задач алгебраич. теории чисел. Задача нахождения расширений Галуа с абелевой Г. <г. (абелевы расширения) относится к теории нолей классов. Г. г. полей алгебраич. функций изучаются в алгебраич. геометрии.

Если L- поле и G - конечная подгруппа группы автоморфизмов поля L, то Lявляется расширением Галуа поля инвариантов , Г. г. этого расширения изоморфна G; при этом степень расширения равна порядку группы G.

Фундаментальным результатом о Г. г. является следующая теорема, иногда наз. основной теоремой о расширениях Галуа (или теоремой о соответствии Галуа). Если L- расширение Галуа конечной степени поля k, то существует взаимное однозначное соответствие между всеми подгруппами НГ. г. 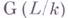и всеми подполями Fполя L, содержащими k, причем соответствующие друг другу H и F таковы, что F - поле инвариантов H, a Н - группа Галуа L/F (см. Галуа соответствие). Эта теорема имеет многочисленные аналоги во многих математич. теориях, так существует ее обобщение на случай расширений бесконечной степени (см. Галуа топологическая группа). Имеется обобщение понятия Г. г. на случай расширений произвольных коммутативных колец и даже схем (см. Фундаментальная группа), а также на случай расширений тел.

Лит.:[1] Бурбаки Н., Алгебра. Многочлены и поля. Упорядоченные группы, пер. с франц., М., 1965; [2] Ленг С., Алгебра, пер. с англ., М., 1968; [3] Постников М. М., Теория Галуа, М., 1963; [4] Джекобсон Н., Теория колец, пер. с англ., М., 1947. И. В. Долгачев.