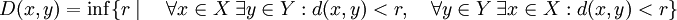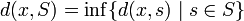- Полное метрическое пространство
-
Метри́ческим простра́нством называется множество, в котором определено расстояние между любой парой элементов.
Содержание
Формальное определение
Метрическое пространство M есть множество точек с функцией расстояния (также называется метрикой)
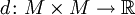 (где
(где  обозначает множество вещественных чисел). Для любых точек x,y,z из M эта функция должна удовлетворять следующим условиям:
обозначает множество вещественных чисел). Для любых точек x,y,z из M эта функция должна удовлетворять следующим условиям: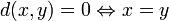 (аксиома тождества).
(аксиома тождества).- d(x,y) = d(y,x) (аксиома симметрии).
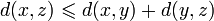 (аксиома треугольника или неравенство треугольника).
(аксиома треугольника или неравенство треугольника).
Эти аксиомы отражают интуитивное понятие расстояния. Например, расстояние должно быть неотрицательно, то есть
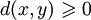 (это вытекает из аксиомы треугольника при z = x) и расстояние от x до y такое же, как и от y до x. Неравенство треугольника означает, что пройти от x до z можно короче, или хотя бы не длиннее, чем сначала пройти x до y, а потом от y до z.
(это вытекает из аксиомы треугольника при z = x) и расстояние от x до y такое же, как и от y до x. Неравенство треугольника означает, что пройти от x до z можно короче, или хотя бы не длиннее, чем сначала пройти x до y, а потом от y до z.Обозначения
Обычно расстояние между точками x и y в метрическом пространстве M обозначается
- d(x,y),
- | xy | или | xy | M , если необходимо подчеркнуть что речь идет о M,
- xy
- | x − y |
Примеры
- Дискретная метрика: d(x,y) = 0, если x = y, и d(x,y) = 1 во всех остальных случаях.
- Вещественные числа с функцией расстояния d(x,y) = | y − x | и евклидово пространство являются полными метрическими пространствами.
- Манхеттенская, или городская метрика: координатная плоскость, на которой расстояние определено как сумма расстояний между координатами. Более общий пример: любое нормированное пространство можно превратить в метрическое, определив функцию расстояния
 , в случае конечной размерности это называется пространством Минковского[1] (не надо путать с другим пространством Минковского).
, в случае конечной размерности это называется пространством Минковского[1] (не надо путать с другим пространством Минковского).
- Так называемая Французская железнодорожная метрика является примером, который нередко приводят в качестве примера метрики, не порожденной нормой.
- Любое связное риманово многообразие M можно превратить в метрическое пространство, определив расстояние как точную нижнюю грань длин путей, соединяющих пару точек.
- Множество вершин любого связного графа G можно превратить в метрическое пространство, определив расстояние как минимальное число рёбер в пути, соединяющем вершины.
- Множество компактных подмножеств K(M) любого метрического пространства M можно превратить в метрическое пространство, определив расстояние с помощью так называемой метрики Хаусдорффа. В этой метрике два подмножества близки друг к другу, если для любой точки одного множества можно найти близкую точку в другом подмножестве. Вот точное определение:
- Множество всех компактных метрических пространств (с точностью до изометрии) можно превратить в метрическое пространство, определив расстояние с помощью так называемой метрики Громова — Хаусдорффа.
Связанные определения
- Метрическое пространство называется полным, если любая фундаментальная последовательность в нём сходится к некоторому элементу этого пространства.
- Метрика d на M называется внутренней, если любые две точки x и y в M можно соединить кривой с длиной, произвольно близкой к d(x,y).
- Любое метрическое пространство обладает естественной топологией, базой для которой служит множество открытых шаров, т.е. множеств следующего типа:
-
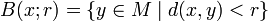 ,
,
- где x есть точка в M и r — положительное вещественное число, называемое радиусом шара. Иначе говоря, множество O является открытым, если для любой точки
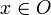 найдётся положительное число r, такое, что множество точек на расстоянии меньше r от x принадлежит O.
найдётся положительное число r, такое, что множество точек на расстоянии меньше r от x принадлежит O.
- Две метрики, определяющие одну и ту же топологию, называются эквивалентными.
- Топологическое пространство, которое может быть получено таким образом, называется метризируемым.
- Расстояние d(x,S) от точки x до подмножества S в M определяется по формуле:
-
- Тогда d(x,S) = 0, только если x принадлежит замыканию S.
Свойства
- Метрическое пространство компактно тогда и только тогда, когда из любой последовательности точек можно выбрать сходящуюся подпоследовательность (секвенциальная компактность).
- Метрическое пространство может не иметь счётной базы, но всегда удовлетворяет первой аксиоме счётности — имеет счётную базу в каждой точке.
- Более того, каждый компакт в метрическом пространстве имеет счётную базу окрестностей.
- Сверх того, в каждом метрическом пространстве существует такая база, что каждая точка пространства принадлежит лишь счётному множеству её элементов — точечно-счётная база (но это свойство слабее метризуемости даже в присутствии паракомпактности и хаусдорфовости).
Вариации и обобщения
Для данного множества
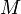 , функция
, функция 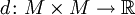 называется псевдометрикой или полуметрикой на
называется псевдометрикой или полуметрикой на 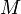 если для любых точек
если для любых точек  из
из 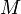 она удовлетворяет следующим условиям:
она удовлетворяет следующим условиям: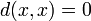 ;
;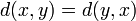 (симметрия);
(симметрия);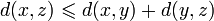 (неравенство треугольника).
(неравенство треугольника).
То есть, в отличие от метрики, различные точки в
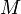 могут находится на нулевом расстоянии. Псевдометрика естественно определяет метрику на факторпространстве
могут находится на нулевом расстоянии. Псевдометрика естественно определяет метрику на факторпространстве 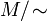 где
где 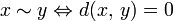 .
.Метрика на пространстве называется ультраметрикой, если она удовлетворяет сильному неравенству треугольника:
-
-
-
- Для всех
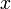 ,
, 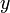 и
и 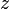 в
в 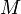
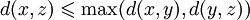 .
.
- Для всех
-
-
Иногда рассматривают метрики со значениями
![[0;\infty]](/pictures/wiki/files/54/6ac441d46ab9a3b004180c27a3d5361f.png) , соответствующие пространства называются
, соответствующие пространства называются 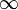 -метрическими пространствами. Для любой такой метрики можно рассмотреть конечную метрику
-метрическими пространствами. Для любой такой метрики можно рассмотреть конечную метрику 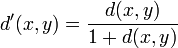 или
или 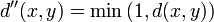 . Эти метрические пространства имеют одну и ту же топологию.
. Эти метрические пространства имеют одну и ту же топологию.История
Морис Фреше впервые ввёл понятие метрического пространства[2] в связи с рассмотрением функциональных пространств.
Примечания
См. также
Литература
- Н.Васильев,
- Метрические пространства Квант, №1, 1990;
- Метрические пространства Квант, №10, 1970.
- В.А.Скворцов, Примеры метрических пространств, Библиотека «Математическое просвещение», выпуск 9, (2001).
- Ю.А.Шрейдер Что такое расстояние?, «Популярные лекции по математике», Выпуск 38, Физматгиз 1963 г., 76 стр.
Ссылки
Wikimedia Foundation. 2010.