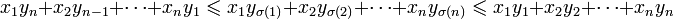Неравенство об одномонотонных последовательностях

Перестановочное неравенство, или неравенство об одномонотонных последовательностях, или «транс-неравенство», утверждает, что скалярное произведение двух наборов чисел является максимальным возможным, если наборы одномонотонны (то есть оба одновременно неубывающие или одновременно невозврастающие), и минимально возможным, если наборы противоположной монотонности (то есть один неубывающий, другой невозврастающий).

Другими словами, если 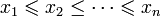$x_1\leqslant x_2 \leq \dots\leqslant x_n$ и $y_1\leqslant y_2 \leq \dots\leqslant y_n$, то для произвольной перестановки σ чисел $\{1,2,\dots,n\}$ выполняется неравенство:

$x_1 y_n + x_2 y_{n-1} + \cdots + x_n y_1 \leqslant x_1 y_{\sigma(1)} + x_2 y_{\sigma(2)} + \cdots + x_n y_{\sigma(n)} \leqslant x_1 y_1 + x_2 y_2 + \cdots + x_n y_n$

Следствием перестановочного неравенства является неравенство Чебышёва для сумм.

Попытки обобщения

Для 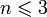$n\leqslant 3$ и двух наборов вещественных чисел $x_1\leqslant\cdots\leqslant x_n$ и $y_1\leqslant\cdots\leqslant y_n$,

$x_1 y_{\sigma (1)} + \cdots + x_n y_{\sigma (n)} \leqslant x_1 y_{\pi(1)} + \cdots + x_n y_{\pi(n)}$

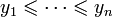если число инверсий в перестановке π меньше чем в перестановке σ. В частности, у тождественной перестановки число инверсий равно нулю, а у перестановки 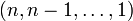$(n,n-1,\dots,1)$ число инверсий максимально.

Первоначальная публикация обобщённого перестановочного неравенства (Scripta Mathematica 1946, 12(2), 164—169) утверждала, что оно справедливо для всех натуральных n, однако при 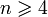$n\geqslant 4$ к нему существуют контрпримеры, в частности для наборов 0,1,2,3 и 0,1,2,10:

$0\cdot0+1\cdot1+2\cdot10+3\cdot2=27 < 31= 0\cdot 2+1\cdot 1+2\cdot 0+3\cdot 10$

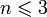При $n\leqslant 3$ неравенство совпадает с обычным перестановочным неравенством.

Ссылки

• Л. В. Радзивиловский «Обобщение перестановочного неравенства и монгольское неравенство». Сборник «Математическое Просвещение». Третья серия. Выпуск 10, 2006.