Неравенство между средним геометрическим и средним арифметическим
- Неравенство между средним геометрическим и средним арифметическим
-
Неравенство Коши (неравенство о среднем арифметическом и среднем геометрическом) Для любых неотрицательных чисел 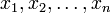 верно неравенство:
верно неравенство:

причем равенство достигается тогда и только тогда, когда  .
.
Выражение

называется средним арифметическим, а
![\bar{x}_\mathrm{geom} = \sqrt[n]{\prod_{i=1}^n{x_i}} = \sqrt[n]{x_1\cdot x_2\cdots x_n}](/pictures/wiki/files/54/6b1b069fc00d94152289bc729b46fefa.png)
средним геометрическим чисел 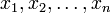 .
.
Связанные результаты
- Неравенство между средним арифметическим и средним геометрическим является частным случаем неравенства о средних.
История
Одно из доказательств этого неравенства было опубликовано Коши в его учебнике по математическому анализу в 1821 году.
Ссылки
Статья в физико-математическом журнале "Квант"
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Неравенство между средним геометрическим и средним арифметическим" в других словарях:
Неравенство между средним арифметическим и средним геометрическим — Неравенство Коши (неравенство о средних) Для любых неотрицательных чисел верно неравенство: причем равенство достигается тогда и только тогда, когда . Выражение называется средним арифметическим, а … Википедия
Неравенство Йенсена — обобщает тот факт, что секущая графика выпуклой функции находится над графиком. Неравенство Йе … Википедия
Неравенство о средних — Среднее степени d (или просто среднее степенное) набора положительных вещественных чисел определяется как При этом по непрерывности доопределяются следующие величины … Википедия
Коши неравенство — Название «Неравенство Коши» может относиться к одному из следующих неравенств: Неравенство Коши Буняковского Неравенство между средним арифметическим и средним геометрическим … Википедия
ИЕНСЕНА НЕРАВЕНСТВО — в простейшей дискретной форме: где f(x) выпуклая (см. Выпуклая функция )на нек ром множестве Сфункция, i=1, 2, . . ., n, Равенство достигается тогда и только тогда, когда либо х 1=x2=. . . = xn, либо f(x). линейная функция. И н те тральное И. н.… … Математическая энциклопедия
Среднее геометрическое — Средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось. Более формально: Среднее геометрическое двух чисел также называется… … Википедия
Среднее степенное — У этого термина существуют и другие значения, см. среднее значение. Среднее степени d (или просто среднее степенное) набора положительных вещественных чисел определяется как При этом по непрерывности доопределяются следующие величины … Википедия
Среднее арифметическое — У этого термина существуют и другие значения, см. среднее значение. В математике и статистике среднее арифметическое одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений деленную на их… … Википедия
Коши, Огюстен Луи — Огюстен Луи Коши Augustin Louis Cauchy … Википедия
Коши, Огюстен — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия
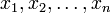 верно неравенство:
верно неравенство: .
.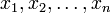 .
.


![\bar{x}_\mathrm{geom} = \sqrt[n]{\prod_{i=1}^n{x_i}} = \sqrt[n]{x_1\cdot x_2\cdots x_n}](/pictures/wiki/files/54/6b1b069fc00d94152289bc729b46fefa.png)