Монте-Карло (метод)

Ме́тод Мо́нте-Ка́рло (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в областях физики, математики, экономики, оптимизации, теории управления и др.

История

Алгоритм Буффона для определения числа Пи

Случайные величины использовались для решения различных прикладных задач достаточно давно. Примером может служить способ определения числа Пи, который был предложен Буффоном еще в 1777 году. Суть метода была в бросании иглы длиной L на плоскость, расчерченную параллельными прямыми, расположенными на расстоянии r друг от друга (см. Рис. 1).

Рисунок 1. Метод Буффона

Вероятность (как видно из дальнейшего контекста, речь идёт не о вероятности, а о математическом ожидании количества пересечений за один опыт; вероятностью это становится лишь при условии, что r > L) того, что отрезок пересечет прямую, связана с числом Пи:

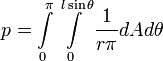$p=\int\limits_{0}^{\pi} \int\limits_{0}^{l\sin{\theta}} \frac{1}{r\pi}dAd\theta$, где

• A — расстояние от начала иглы до ближайшей к ней прямой;
• θ — угол иглы относительно прямых.

Этот интеграл просто взять: 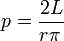$p=\frac{2L}{r\pi\,}$ (при условии, что r > L), поэтому подсчитав долю отрезков, пересекающих прямые, можно приближенно определить это число. При увеличении количества попыток точность получаемого результата будет увеличиваться.

В 1864 году капитан Фокс, выздоравливая после ранения, чтобы как-то занять себя, реализовал эксперимент по бросанию иглы. Результаты представлены в следующей таблице:

	Число бросаний	Число пересечений	Длина иглы	Расстояние между прямыми	Вращение	Значение Пи
Первая попытка	500	236	3	4	отсутствует	3.1780
Вторая попытка	530	253	3	4	присутствует	3.1423
Третья попытка	590	939	5	2	присутствует	3.1416

Комментарии:

• Вращение плоскости применялось (и как показывают результаты — успешно) для того, чтобы уменьшить систематическую ошибку.
• В третьей попытке длина иглы была больше расстояния между линиями, что позволило не увеличивая числа бросаний эффективно увеличить число событий и повысить точность.

Связь стохастических процессов и дифференциальных уравнений

Создание математического аппарата стохастических методов началось в конце 19-го века. В 1899 году лорд Релей показал, что одномерное случайное блуждание на бесконечной решётке может давать приближенное решение параболического дифференциального уравнения. Андрей Колмогоров в 1931 году дал большой толчок развитию стохастических подходов к решению различных математических задач, поскольку он сумел доказать, что цепи Маркова связаны с некоторыми интегро-дифференциальными уравнениями. В 1933 году Иван Петровский показал, что случайное блуждание, образующее Марковскую цепь, асимптотически связано с решением эллиптического дифференциального уравнения в частных производных. После этих открытий стало понятно, что стохастические процессы можно описывать дифференциальными уравнениями и, соответственно, исследовать при помощи хорошо на тот момент разработанных математических методов решения этих уравнений.

Рождение метода Монте-Карло в Лос-Аламосе

Сначала Энрико Ферми в 1930-х годах в Италии, а затем Джон фон Нейман и Станислав Улам в 1940-х в Лос-Аламосе предположили, что можно использовать связь между стохастическими процессами и дифференциальными уравнениями «в обратную сторону». Они предложили использовать стохастический подход для аппроксимации многомерных интегралов в уравнениях переноса, возникших в связи с задачей о движении нейтрона в изотропной среде.

Идея была развита Уламом, который, по иронии судьбы, также как и Фокс боролся с вынужденным бездельем во время выздоровления после болезни, и, раскладывая пасьянсы, задался вопросом, какова вероятность того, что пасьянс «сложится». Ему в голову пришла идея, что вместо того, чтобы использовать обычные для подобных задач соображения комбинаторики, можно просто поставить «эксперимент» большое число раз и, таким образом, подсчитав число удачных исходов, оценить их вероятность. Он же предложил использовать компьютеры для расчётов методом Монте-Карло.

Появление первых электронных компьютеров, которые могли с большой скоростью генерировать псевдослучайные числа, резко расширило круг задач, для решения которых стохастический подход оказался более эффективным, чем другие математические методы. После этого произошёл большой прорыв и метод Монте-Карло применялся во многих задачах, однако его использование не всегда было оправдано из-за большого количества вычислений, необходимых для получения ответа с заданной точностью.

Годом рождения метода Монте-Карло считается 1949 год, когда в свет выходит статья Метрополиса и Улама «Метод Монте-Карло». Название метода происходит от названия города в княжестве Монако, широко известного своими многочисленными казино, поскольку именно рулетка является одним из самых широко известных генераторов случайных чисел. Станислав Улам пишет в своей автобиографии «Приключения математика», что название было предложено Николасом Метрополисом в честь его дяди, который был азартным игроком.

Дальнейшее развитие и современность

В 1950-х годах метод использовался для расчётов при разработке водородной бомбы. Основные заслуги в развитии метода в это время принадлежат сотрудникам лабораторий ВВС США и корпорации RAND.

В 1970-х годах в новой области математики — теории вычислительной сложности было показано, что существует класс задач, сложность (количество вычислений, необходимых для получения точного ответа) которых растёт с размерностью задачи экспоненциально. Иногда можно, пожертвовав точностью, найти алгоритм, сложность которого растёт медленнее, но есть большое количество задач, для которого этого нельзя сделать (например, задача определения объёма выпуклого тела в n-мерном евклидовом пространстве) и метод Монте-Карло является единственной возможностью для получения достаточно точного ответа за приемлемое время. В настоящее время основные усилия исследователей направлены на создание эффективных Монте-Карло алгоритмов различных физических, химических и социальных процессов для параллельных вычислительных систем.

Интегрирование методом Монте-Карло

Рисунок 2. Численное интегрирование функции детерминистическим методом

Предположим, необходимо взять интеграл от некоторой функции. Воспользуемся неформальным геометрическим описанием интеграла и будем понимать его как площадь под графиком этой функции.

Для определения этой площади можно воспользоваться одним из обычных численных методов интегрирования: разбить отрезок на подотрезки, подсчитать площадь под графиком функции на каждом из них и сложить. Предположим, что для функции, представленной на рисунке 2, достаточно разбиения на 25 отрезков и, следовательно, вычисления 25 значений функции. Представим теперь, мы имеем дело с n-мерной функцией. Тогда нам необходимо 25ⁿ отрезков и столько же вычислений значения функции. При размерности функции больше 10 задача становится огромной. Поскольку пространства большой размерности встречаются, в частности, в задачах теории струн, а также многих других физических задачах, где имеются системы со многими степенями свободы, необходимо иметь метод решения, вычислительная сложность которого бы не столь сильно зависела от размерности. Именно таким свойством обладает метод Монте-Карло.

Обычный алгоритм Монте-Карло интегрирования

Рисунок 3. Численное интегрирование функции методом Монте-Карло

Для определения площади под графиком функции можно использовать следующий стохастический алгоритм:

• ограничим функцию прямоугольником (n-мерным параллелепипедом в случае многих измерений), площадь которого S_par можно легко вычислить;
• «набросаем» в этот прямоугольник (параллелепипед) некоторое количество точек (N штук), координаты которых будем выбирать случайным образом;
• определим число точек (K штук), которые попадут под график функции;
• площадь области, ограниченной функцией и осями координат, S даётся следующим выражением $S =S_{par}\frac{K}{N}$

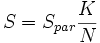
Для малого числа измерений интегрируемой функции производительность Монте-Карло интегрирования гораздо ниже, чем производительность детерминированных методов. Тем не менее, в некоторых случаях, когда функция задана неявно, а необходимо определить область, заданную в виде сложных неравенств, стохастический метод может оказаться более предпочтительным.

Использование выборки по значимости

Очевидно, что точность вычислений можно увеличить, если область, ограничивающая искомую функцию, будет максимально к ней приближена. Для этого необходимо использовать случайные величины с распределением, форма которого максимально близка к форме интегрируемой функции. На этом основан один из методов улучшения сходимости в вычислениях методом Монте-Карло: выборка по значимости.

Оптимизация

Применение в физике

Компьютерное моделирование играет в современной физике важную роль и метод Монте-Карло является одним из самых распространённых во многих областях от квантовой физики до физики твёрдого тела, физики плазмы и астрофизики.

Алгоритм Метрополиса

Традиционно метод Монте-Карло применялся для определения различных физических параметров систем, находящихся в состоянии термодинамического равновесия. Предположим имеется набор W(S) возможных состояний физической системы S. Для определения среднего значения 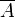$\overline{A}$ некоторой величины A необходимо рассчитать 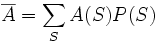$\overline{A}=\sum_{S} A(S)P(S)$, где суммирование производится по всем состояниям S из W(S), P(S) — вероятность состояния S.

Динамическая (кинетическая) формулировка

Прямое моделирование методом Монте-Карло

Прямое моделирование методом Монте-Карло какого-либо физического процесса подразумевает моделирование поведения отдельных элементарных частей физической системы. По сути это прямое моделирование близко к решению задачи из первых принципов, однако обычно для ускорения расчётов допускается применение каких-либо физических приближений. Примером могут служить расчёты различных процессов методом молекулярной динамики: с одной стороны система описывается через поведение её элементарных составных частей, с другой стороны, используемый потенциал взаимодействия зачастую является эмпирическим.

Примеры прямого моделирования методом Монте-Карло:

• Моделирование облучения твёрдых тел ионами в приближении бинарных столкновений.
• Прямое Монте-Карло моделирование разреженных газов.
• Большинство кинетических Монте-Карло моделей относятся к числу прямых (в частности, исследование молекулярно-пучковой эпитаксии).

Квантовый метод Монте-Карло

Квантовый метод Монте-Карло широко применяется для исследования сложных молекул и твёрдых тел. Это название объединяет несколько разных методов. Первый из них это вариационный метод Монте-Карло, который по сути является численным интегрированием многомерных интегралов, возникающих при решении уравнения Шрёдингера. Для решения задачи, в которой участвует 1000 электронов, необходимо взятие 3000-мерных интегралов, и при решении таких задач метод Монте-Карло имеет огромное преимущество в производительности по сравнению с другими численными методами интегрирования. Другая разновидность метода Монте-Карло — это диффузионный метод Монте-Карло, который, впрочем, не очень рационален.

См. также

• Лас-Вегас (алгоритм)
• Генераторы псевдослучайных чисел
• Программа MCU

Ссылки

• Статья «Моделируя жизнь», автор Андрей Тепляков
• N. Metropolis, S. Ulam The Monte Carlo Method, — J. Amer. statistical assoc. 1949 44 № 247 335—341.
• Книга «Fundamentals of the Monte Carlo method for neutral and charged particle transport», автор Alex F Bielajew (на английском)
• W. M. C. Foulkes, L. Mitas, R. J. Needs and G. Rajagopal Quantum Monte Carlo simulations of solids, — Reviews of Modern Physics 73 (2001) 33.
• Статья «Metopolis, Monte Carlo and the MANIAC»
• Статья о Монте-Карло на www.riskglossary.com