- МОНТЕ-КАРЛО МЕТОД
метод статистических испытаний,- численный метод, основанный на моделировании случайных величин и построении статистич. оценок для искомых величин. Принято считать, что М.-К. м. возник в 1949 (см. [1]), когда в связи с работами по созданию атомных реакторов Дж. Нейман (J. Neumann) и С. Улам (S. Ulam) предложили использовать аппарат теории вероятностей для решения прикладных задач с помощью ЭВМ. М.-К. м. получил свое название по имени города Монте-Карло, известного своими игорными заведениями.
Моделирование случайных величин с заданными распределениями. Как правило, такое моделирование осуществляется путем преобразования одного или нескольких независимых значений случайного числа
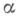 , распределенного равномерно в интервале (0, 1). Последовательности "выборочных" значений
, распределенного равномерно в интервале (0, 1). Последовательности "выборочных" значений  обычно получают на ЭВМ с помощью теоретико-числовых алгоритмов, среди к-рых наибольшее распространение получил т. н. метод вычетов, напр, в таком виде:
обычно получают на ЭВМ с помощью теоретико-числовых алгоритмов, среди к-рых наибольшее распространение получил т. н. метод вычетов, напр, в таком виде: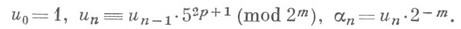
Здесь
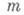 - число разрядов мантиссы ЭВМ, а
- число разрядов мантиссы ЭВМ, а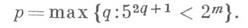
Числа такого типа наз. псевдослучайными числами; они проверяются статистич. тестами и решением типовых задач (см. [2] - [6]). Длина периода для указанного варианта метода вычетов равна
 В М.-К. м. используются также физич. генераторы и таблицы случайных чисел, а также квазислучайные числа. Существуют М.-К. м. с малым числам разыгрываемых параметров (см. [7]).
В М.-К. м. используются также физич. генераторы и таблицы случайных чисел, а также квазислучайные числа. Существуют М.-К. м. с малым числам разыгрываемых параметров (см. [7]).Стандартный метод моделирования дискретной случайной величины
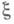 с распределением
с распределением 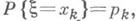
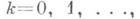 состоит в следующем: полагают
состоит в следующем: полагают  если для выбранного значения
если для выбранного значения 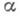 выполняется соотношение
выполняется соотношение
Стандартный метод моделирования непрерывной случайной величины (иногда наз. методом обратной функции) состоит в использовании легко проверяемого представления:
 , где
, где 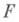 - функция распределения с заданной плотностью
- функция распределения с заданной плотностью 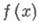 . Иногда полезна рандомизация моделирования (иначе - метод суперпозиции) на основе выражения
. Иногда полезна рандомизация моделирования (иначе - метод суперпозиции) на основе выражения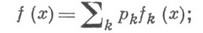
при этом сначала выбирают номер т с распределением
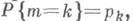 а затем получают выборочное значение
а затем получают выборочное значение 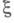 из распределения с плотностью
из распределения с плотностью 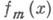 . При других способах рандомизации нек-рые параметры детерминированного способа решения задачи рассматривают как случайные величины (см. [7] - [9]).
. При других способах рандомизации нек-рые параметры детерминированного способа решения задачи рассматривают как случайные величины (см. [7] - [9]).Другим общим методом моделирования непрерывной случайной величины является метод исключения (метод отбора), в основе к-рого лежит утверждение: если точка
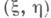 распределена равномерно в области
распределена равномерно в области 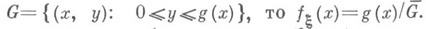 В методе исключения выбирают точку
В методе исключения выбирают точку  равномерно по области
равномерно по области  и полагают
и полагают 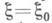 , если
, если  в противном случае повторяют выбор
в противном случае повторяют выбор 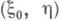 и т. д. Напр., если
и т. д. Напр., если  и
и  то можно полагать
то можно полагать 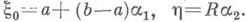 Среднее число операций в методе исключения пропорционально величине
Среднее число операций в методе исключения пропорционально величине 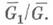
Для многих случайных величин получены специальные представления вида
 Напр., случайные величины
Напр., случайные величины
имеют стандартное нормальное распределение и независимы; случайная величина
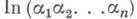 имеет гамма-распределение с параметром п;случайная величина
имеет гамма-распределение с параметром п;случайная величина 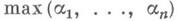 распределена с плотностью
распределена с плотностью 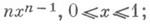 случайная величина
случайная величина  имеет бета-распределение с параметрами р, п (см. [3] - [6]).
имеет бета-распределение с параметрами р, п (см. [3] - [6]).Стандартный алгоритм моделирования непрерывного случайного вектора
 состоит в последовательном выборе значений его компонент из условных распределений соответственно представлению
состоит в последовательном выборе значений его компонент из условных распределений соответственно представлению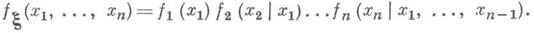
Метод исключения переносится на многомерный случай без изменений, надо лишь в его формулировке рассматривать
 как векторы. Многомерный нормальный вектор можно моделировать с помощью специального линейного преобразования вектора независимых стандартных нормальных случайных величин. Разработаны также специальные приемы приближенного моделирования стационарных гауссовских процессов (см., напр., [3], [6]).
как векторы. Многомерный нормальный вектор можно моделировать с помощью специального линейного преобразования вектора независимых стандартных нормальных случайных величин. Разработаны также специальные приемы приближенного моделирования стационарных гауссовских процессов (см., напр., [3], [6]).Если в расчете по М.-К. м. моделируются случайные величины, определяемые реальным содержанием явления, то расчет представляет собой прямое моделирование (имитацию) этого явления. Разработано моделирование на ЭВМ процессов переноса, рассеяния и размножения частиц: нейтронов, гамма-квантов, фотонов, электронов и др. (см., напр., [11] - [18]); моделирование эволюции ансамблей молекул для решения различных задач классической и квантовой статистич. физики (см., напр., [10], [18]); моделирование массового обслуживания и производственных процессов (см., напр., [2], [6], [18]); моделирование различных случайных процессов в технике, гидрологии, метеорологии, геологии, химии, биологии и т. д. (см. [18]). Алгоритмы моделирования обычно тщательно обрабатывают, напр, табулируют сложные функции, изменяют стандартные процедуры и т. д. Тем не менее часто прямое моделирование не может обеспечить требуемой точности оценок искомых величин. Разработано много способов повышения эффективности моделирования.
Алгоритмы М.-К. м. для оценки многократных интегралов. Пусть необходимо оценить интеграл
 по мере Лебега в евклидовом s-мерном пространстве
по мере Лебега в евклидовом s-мерном пространстве 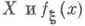 - плотность вероятности такая, что
- плотность вероятности такая, что  можно записать в виде мате-матич. ожидания следующим образом:
можно записать в виде мате-матич. ожидания следующим образом: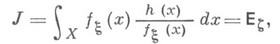
где
 . Моделируя
. Моделируя  на ЭВМ, можно получить Nвыборочных значений
на ЭВМ, можно получить Nвыборочных значений  . В смысле закона больших чисел
. В смысле закона больших чисел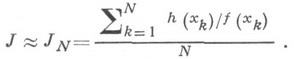
Одновременно можно оценить среднеквадратичную погрешность
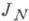 , т. е. величину
, т. е. величину  , и приближенно построить подходящий доверительный интервал для
, и приближенно построить подходящий доверительный интервал для 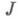 . Выбором плотности f можно распорядиться для получения оценки с возможно меньшей дисперсией. Напр., если
. Выбором плотности f можно распорядиться для получения оценки с возможно меньшей дисперсией. Напр., если 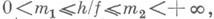 то
то 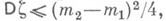 и если
и если  то
то 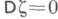 . Соответствующие алгоритмы наз. существенной выборкой (выборкой по важности). Другая общая модификация - метод выделения главной части - строится в тех случаях, когда определена функция
. Соответствующие алгоритмы наз. существенной выборкой (выборкой по важности). Другая общая модификация - метод выделения главной части - строится в тех случаях, когда определена функция  с известным значением интеграла. Иногда полезны сочетания М.-К. м. с классич. квадратурами - т. н. случайные квадратурные формулы, основная идея к-рых состоит в том, что узлы и коэффициенты какой-либо квадратурной суммы (напр., интерполяционной) выбираются случайно из распределения, обеспечивающего несмещенность получаемой оценки интеграла [3]. Частными случаями этих формул являются: т. н. метод слоистой выборки, в к-ром узлы выбираются по одному в каждой части фиксированного разбиения области интегрирования, а коэффициенты пропорциональны соответствующим объемам; так наз. метод симметричной выборки, к-рый в случае интегрирования по интервалу (0, 1) определяется выражением (см. [10])
с известным значением интеграла. Иногда полезны сочетания М.-К. м. с классич. квадратурами - т. н. случайные квадратурные формулы, основная идея к-рых состоит в том, что узлы и коэффициенты какой-либо квадратурной суммы (напр., интерполяционной) выбираются случайно из распределения, обеспечивающего несмещенность получаемой оценки интеграла [3]. Частными случаями этих формул являются: т. н. метод слоистой выборки, в к-ром узлы выбираются по одному в каждой части фиксированного разбиения области интегрирования, а коэффициенты пропорциональны соответствующим объемам; так наз. метод симметричной выборки, к-рый в случае интегрирования по интервалу (0, 1) определяется выражением (см. [10])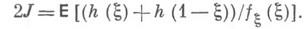
При этом порядок скорости сходимости М.-К. м. повышается и в нек-рых случаях становится максимально возможным на рассматриваемом классе задач.
В общем случае область интегрирования разбивается на параллелепипеды. В каждом параллелепипеде значение интеграла вычисляется через среднее значение в случайной точке и точке, симметричной ей относительно центра параллелепипеда.
Ряд модификаций М.-К. м. основан на (может быть, формальном) представлении искомой величины в виде двукратного интеграла: '

где
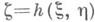 , а вектор
, а вектор 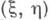 распределен с плотностью
распределен с плотностью 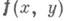 . Известно, что
. Известно, что  и
и 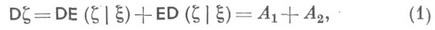
где
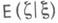 - условное математич. ожидание, а
- условное математич. ожидание, а  - условная дисперсия
- условная дисперсия 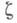 для фиксированного значения
для фиксированного значения 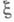 . Формула (1) широко используется в М.-К. м. В частности, она показывает, что
. Формула (1) широко используется в М.-К. м. В частности, она показывает, что  т. е. аналитич. осреднение по какой-либо переменной увеличивает точность М.-К. м. Однако при этом может значительно возрасти объем вычислений. Для ЭВМ время, необходимое для достижения заданной погрешности, пропорционально величине
т. е. аналитич. осреднение по какой-либо переменной увеличивает точность М.-К. м. Однако при этом может значительно возрасти объем вычислений. Для ЭВМ время, необходимое для достижения заданной погрешности, пропорционально величине  , где t- среднее время получения одного значения
, где t- среднее время получения одного значения  . По этому критерию оптимизируется метод расщепления, простейший вариант к-рого состоит в использовании несмещенной оценки:
. По этому критерию оптимизируется метод расщепления, простейший вариант к-рого состоит в использовании несмещенной оценки:
где
 - условно независимы и распределены как
- условно независимы и распределены как  при фиксированном значении
при фиксированном значении 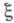 . С помощью (1) можно получить оптимальное значение
. С помощью (1) можно получить оптимальное значение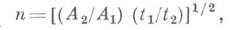
где
 - средние времена ЭВМ, соответствующие выборкам
- средние времена ЭВМ, соответствующие выборкам 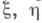 (см., напр., [4]).
(см., напр., [4]).Если подинтегральная функция зависит от параметра, то целесообразно использовать метод зависимых испытаний, т. е. оценивать интегралы для различных значений параметра по одним и тем же случайным узлам [20]. Важным свойством М.-К. м. является сравнительно относительно слабая зависимость среднеквадратич. погрешности
 от числа измерений, причем порядок сходимости по числу узлов
от числа измерений, причем порядок сходимости по числу узлов  всегда один и тот же:
всегда один и тот же:  . Это позволяет оценивать (после предварительных преобразований задачи) интегралы очень высокой и даже бесконечной кратности. Напр., разработана методика оценки интегралов Винера [19].
. Это позволяет оценивать (после предварительных преобразований задачи) интегралы очень высокой и даже бесконечной кратности. Напр., разработана методика оценки интегралов Винера [19].Алгоритмы М.-К. м. для решений интегральных уравнений 2-го рода. Пусть необходимо оценить линейный функционал
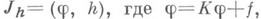 причем для интегрального оператора Кс ядром
причем для интегрального оператора Кс ядром  выполняется условие, обеспечивающее сходимость ряда Неймана:
выполняется условие, обеспечивающее сходимость ряда Неймана: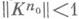 Цепь Маркова
Цепь Маркова 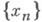 определяется начальной плотностью
определяется начальной плотностью 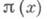 и переходной плотностью
и переходной плотностью  вероятность обрыва цепи в точке
вероятность обрыва цепи в точке 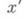 равна
равна  N- случайный номер последнего состояния. Далее определяется функционал от траектории цепи, математич. ожидание к-рого равно
N- случайный номер последнего состояния. Далее определяется функционал от траектории цепи, математич. ожидание к-рого равно 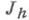 . Чаще всего используется т. Н. оценка по столкновениям
. Чаще всего используется т. Н. оценка по столкновениям
Если
 при
при 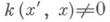 и
и  при
при 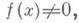 то при нек-ром дополнительном условии
то при нек-ром дополнительном условии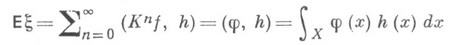
(см. [3]-[5]). Возможность достижения малой дисперсии в знакопостоянном случае показывает следующее утверждение: если
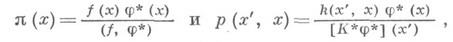 где
где  (см. [4]). Моделируя подходящую цепь Маркова на ЭВМ, получают статистич. оценки линейных функционалов от решения интегрального уравнения 2-го рода. Это дает возможность и локальной оценки решения на основе представления:
(см. [4]). Моделируя подходящую цепь Маркова на ЭВМ, получают статистич. оценки линейных функционалов от решения интегрального уравнения 2-го рода. Это дает возможность и локальной оценки решения на основе представления: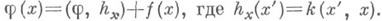 В ряде случаев при решении таких задач наряду с М.-К. м. применяются теоретико-числовые методы (см. [21] ).
В ряде случаев при решении таких задач наряду с М.-К. м. применяются теоретико-числовые методы (см. [21] ).М.-К. м. оценка 1-го собственного значения интегрального оператора осуществляется итерационным методом на основе соотношения [22]:

Все рассмотренные результаты почти автоматически распространяются на системы линейных алгебраич. уравнений вида
 (см. [23]).
(см. [23]).Модификации М.-К. м. в теории переноса излучения (см. [11]-[17]). Для плотности среднего числа столкновений частиц в фазовом пространстве координат
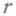 и скоростей
и скоростей  справедливо интегральное уравнение 2-го рода, ядро к-рого в односкоростном случае кмеет вид
справедливо интегральное уравнение 2-го рода, ядро к-рого в односкоростном случае кмеет вид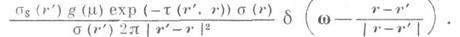
Здесь
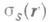 - коэффициент (сечение) рассеяния,-
- коэффициент (сечение) рассеяния,- коэффициент ослабления,
коэффициент ослабления,  - индикатриса рассеяния,
- индикатриса рассеяния,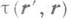 - оптич. длина пути от
- оптич. длина пути от 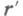 до
до  (см. [3], [4]).
(см. [3], [4]).Для построения оценок с малой дисперсией используются, напр., асимптотич. решения сопряженного уравнения переноса [4]; простейший алгоритм такого типа представляет собой т. н. экспоненциальное преобразование (см. [4], [11]). Разработаны модификации локальной оценки потока частиц (см. [3], [4], [11] - [13], [17], [18]). С помощью моделирования одной цепи Маркова (напр.,. физич. процесса переноса в нек-рой среде) можно одновременно получать зависимые оценки функционалов для различных значений параметров; дифференцируя "веса"
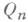 , иногда можно строить несмещенные оценки соответствующих производных (см. [4], [12]). Это дает возможность использовать М.-К. м. при решении нек-рых обратных задач [12]. Для решения ряда задач теории переноса эффективно используется "расщепление" траекторий и аналитич. осреднение [11]. Моделирование траекторий частиц в сложных средах иногда существенно упрощается методом максимального сечения (см. [3]-[5]).
, иногда можно строить несмещенные оценки соответствующих производных (см. [4], [12]). Это дает возможность использовать М.-К. м. при решении нек-рых обратных задач [12]. Для решения ряда задач теории переноса эффективно используется "расщепление" траекторий и аналитич. осреднение [11]. Моделирование траекторий частиц в сложных средах иногда существенно упрощается методом максимального сечения (см. [3]-[5]).Алгоритмы М.- К. м. для решения уравнении эллиптического типа строятся на основе соответствующих интегральных соотношений. Напр., стандартная пятиточечная разностная аппроксимация для уравнения Лапласа имеет вид формулы полного математич. ожидания, соответствующей симметричному блужданию по сетке с поглощением на границе (см., напр., [2], [3]). Непрерывным аналогом этой формулы является соотношение
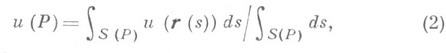
где интеграл берется по поверхности сферы, целиком лежащей в заданной области, с центром в точке Р. Формула (2) и другие аналогичные соотношения дают возможность использовать процесс изотропного "блуждания по сферам" для решения эллиптич. и параболич. уравнений (см. [24], [4]). М.-К. м. эффективен, напр., для оценки решения многомерной краевой задачи в одной точке.
Моделирование марковских ветвящихся процессов позволяет строить оценки решения нек-рых нелинейных уравнений, напр, уравнения Больцмана в теории разреженных газов [3].
Лит.:[1] Neumann J., "NBS Appl. Math, scries", 1951 № 12, p. 36-38; [2] Бусленко Н. П. [и др.], Метод статистических испытаний (метод Монте-Карло), М., 1962; [3] Ермаков С. М., Метод Монте-Карло и смежные вопросы, М., 1971; [4] Михайлов Г. А., Некоторые вопросы теории методов Монте-Карло, Новосиб., 1971; [5] Соболь И. М., Численные методы Монте-Карло, М., 1973; [6] Полляк Ю. Г., Вероятностное моделирование на электронных вычислительных машинах, М., 1971; [7] Бахвалов Н. С, в сб.: Численные методы решения дифференциальных и интегральных уравнений и квадратурные формулы, М., 1964, с. 5-63; [8] его же, "Ж. вычисл. матем. и матем. физики", 1961, т. 1, № 1, с. 64-77; [9] его же, "Вестник МГУ. Сер. матем., механики, астрономии, физ., хим.", 1959, Mi 4, с. 3-18; [10] Hammers-1 е у J. M., Handscomb D. С, Monte Carlo methods, L.- N. Y-, 1964; [11] Метод Монте-Карло в проблеме переноса излучений, М., 1967; [12] Марчук Г. И. [и др.], Метод Монте-Карло в атмосферной оптике, Новосиб., 1976; [13] Спанье Дж.,Гелбард Э., Метод Монте-Карло и задачи переноса нейтронов, пер. с англ., М., 1972; [14]ЧавчанидзеВ. В., "Изв. АН СССР. Сер. физ.", 1955, т. 19, № 6, с. 629 - 38; [15] Прохождение излучений через неоднородности в защите, М., 1968; [16] Франк-Каменецкий А. Д., "Атомная энергия", 1964, т. 16, Mi 2, с. 119-22; [17] Kalos М. Н., "Nuclear Sci. and Eng.", 1968, v. 33, p. 284-90; [18] Методы Монте-Карло и их применения. Тезисы докл. на III Всесоюзн. конф. по методам Монте-Карло, Новосиб., 1971; [19] Гельфанд И. М., Фролов А. С, Ченцов Н. Н., "Изв. вузов. Сер. матем.", 1958, № 5, с. 32-45; [20] Фролов А. С, Ченцов Н. Н., "Ж. вычисл. матем. и матем. физ.", 1962, т. 2, Ms 4, с. 714-17; [21] Коробов Н. М., Теоретикочисло-вые методы в приближенном анализе, М., 1963; [22] Владимиров В. С, "Теория вероятн. и ее примен.", 1956, т. 1, в. 1, с. 113-30; [23] Curtiss J. H., "J. Math. Phys.", 1954, v. 32, № 4, p. 209 - 32; [24] Muller M. E., "Ann. Math. Stat.", 1956, v. 27, № 3, p. 560 - 89.
Г. А. Михайлов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
