Система координат

Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.

В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.

В географии координаты — широта, долгота и высота над известным общим уровнем (например, океана). См. географические координаты.

В астрономии координаты — величины, при помощи которых определяется положение звезды, например, прямое восхождение и склонение.

Небесные координаты — числа, с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой систему полярных координат на сфере с соответствующим образом выбранным полюсом. Систему небесных координат задают большим кругом небесной сферы (или его полюсом, отстоящим на 90° от любой точки этого круга) с указанием на нём начальной точки отсчёта одной из координат. В зависимости от выбора этого круга системы небесных координат называлась горизонтальной, экваториальной, эклиптической и галактической.

Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.

Список наиболее распространённых систем координат

• Аффинная (косоугольная) система координат
• Барицентрические координаты
• Биангулярные координаты
• Биполярные координаты
• Бицентрические координаты
• Бицилиндрические координаты
• Конические координаты
• Координаты Риндлера — в пространстве Минковского
• Параболические координаты
• Полярная система координат
• Проективные координаты
• Прямоугольная (Декартова) система координат
• Сферическая система координат
• Тороидальная система координат
• Трилинейные координаты
• Цилиндрическая система координат
• Цилиндрические параболические координаты
• Эллипсоидальные координаты (эллиптические координаты)

Основные системы

В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.

Декартовы координаты

Основная статья: Прямоугольная система координат

Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел $(x, y)$:

• $x$ — расстояние от точки P до оси y с учетом знака
• $y$ — расстояние от точки P до оси x с учетом знака

В пространстве же необходимо уже 3 координаты $(x, y, z)$:

• $x$ — расстояние от точки P до плоскости yz
• $y$ — расстояние от точки P до плоскости xz
• $z$ — расстояние от точки P до плоскости xy

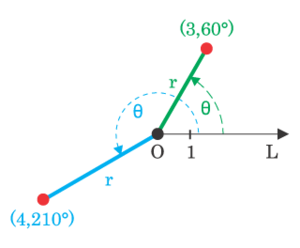
Полярные координаты

Полярные координаты.

Основная статья: Полярная система координат

В полярной системе координат положение точки определяется расстояние до центра координат и углом радиус-вектора с осью Ox.

Термин «полярные координаты» используется только на плоскости, в пространстве применяются цилиндрические и сферические системы координат.

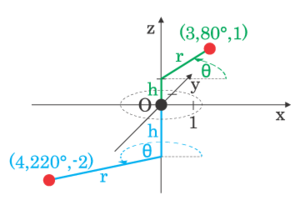
Цилиндрические координаты

Цилиндрические координаты.

Основная статья: Цилиндрическая система координат

Цилиндрические координаты — трехмерный аналог полярных, в котором точка P представляется трехкомпонентным кортежем $(r, \theta, h)$. В терминах декартовой системы координат,

• $0\leq{r}$ (радиус) — расстояние от оси z к точке P,
• $0\leq\theta<360^\circ$ (азимут или долгота) — угол между положительной («плюсовой») частью оси x и прямой линии, мысленно проведённой от полюса до точки P, спроектирован на xy-плоскость
• $h$ (высота) — расстояние (с учетом знака) от xy-плоскости до точки P.

Примечание: в литературе можно встретить пометку z для h; это не принципиально, но нужно следить, какие отметки применяются.

Полярные координаты имеют один недостаток: значение θ теряет смысл, если r = 0.

Цилиндрические координаты полезны для изучения систем, симметричных вокруг некой оси. Например, длинный цилиндр в декартовых координатах имеет уравнение $2x+2y=2c$, тогда как в цилиндрических оно выглядит как r = c

Сферические координаты

Сферические координаты.

Основная статья: Сферическая система координат

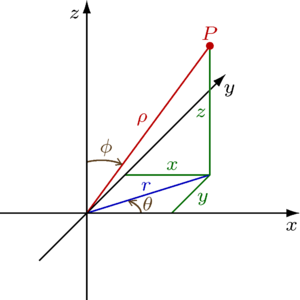
Сферические координаты — трехмерный аналог полярных

Обозначения, принятые в Америке

В сферической системе координат, расположение точки P определяется тремя компонентами: $(\rho, \phi, \theta)$. В терминах декартовой системы координат,

• $0\leq\rho$ (радиус) — это расстояние от точки Р до полюса,
• $0\leq\phi\leq 180^\circ$ (широта или полярный угол) — угол между z-осью и прямой, проведённой из полюса до точки P
• $0\leq\theta<360^\circ$ (азимут или долгота) — угол между положительной («плюсовой» x-осью и проекцией прямой, проведённой из полюса до точки P на xy-плоскость.

Примечание: в литературе можно встретить пометку φ или θ, а также r для ρ;

Сферическая система координат также имеет недостаток: φ теряет смысл если ρ = 0, также и θ теряет смысл, если ρ = 0 или φ = 0 или φ = 180°.

Для построения точки по её сферическими координатами, нужно: от полюса отложить отрезок, равный ρ вдоль положительной z-оси, вернуть его на угол φ вокруг оси y в направлении положительной x-оси, и вернуть на угол θ вокруг z-оси в направлении положительной y-оси.

Сферические координаты полезны при изучении систем, симметричных вокруг точки. Так, уравнение сферы в декартовых координатах выглядит как $x^2+y^2+z^2=c^2$, тогда как в сферических становится намного проще: $\rho=c$.

Европейские обозначения

В Европе принято использовать другие обозначения. Положение точки задаётся числами: $(r, \theta, \varphi)$ , Где r — расстояние от точки до начала координат, $\theta$ — полярный угол, который изменяется в пределах от 0 до π, $\varphi$ — Азимутальный угол, который изменяется в пределах от 0 до 2π. То есть, в европейской системе, которая применяется также и в России, обозначения для углов переставлены по сравнению с американской.

Переход из одной системы координат в другую

Декартовы и полярные

$x=r\,\cos\theta \quad$

$y=r\,\sin\theta \quad$

$r=\sqrt{x^2 + y^2}$

$\theta = \arctan\frac{y}{x} + \pi u_0(-x) \, \operatorname{sgn} y$

где u₀ — функция Хевисайда с $u_0(0)=0$, а sgn — функция signum . Здесь функции u₀ и sgn используются как «логические» переключатели, аналогичные по значению операторам «если .. то» (if…else) в языках программирования. Некоторые языки программирования имеют специальную функцию atan2 (y, x), которая находит правильный θ в необходимом квадранте, определённом x и y.

Декартовы и цилиндрические

$x=r\,\cos\theta$

$y=r\,\sin\theta$

$z=h \quad$

$r=\sqrt{x^2 + y^2}$

$\theta =\arctan\frac{y}{x} + \pi u_0(-x) \, \operatorname{sgn} y$

$h=z \quad$

$\begin{vmatrix}dx\\dy\\dz\end{vmatrix}= \begin{vmatrix} \cos\theta&-r\sin\theta&0\\ \sin\theta&r\cos\theta&0\\ 0&0&1 \end{vmatrix}\cdot \begin{vmatrix}dr\\d\theta\\dh\end{vmatrix}$

$\begin{vmatrix}dr\\d\theta\\dh\end{vmatrix}= \begin{vmatrix} \frac{x}{\sqrt{x^2+y^2}}&\frac{y}{\sqrt{x^2+y^2}}&0\\ \frac{-y}{x^2+y^2}&\frac{x}{x^2+y^2}&0\\ 0&0&1 \end{vmatrix}\cdot \begin{vmatrix}dx\\dy\\dz\end{vmatrix}$

Декартовы и сферические

Уравнения для американских обозначений

${x}=\rho \, \sin\phi \, \cos\theta \quad$

${y}=\rho \, \sin\phi \, \sin\theta \quad$

${z}=\rho \, \cos\phi \quad$

${\rho}=\sqrt{x^2+y^2+z^2}$

${\phi}=\arccos\frac{z}{\rho}$

${\phi}=\arctan\frac{\sqrt{x^2+y^2}}{z}$

${\theta} =\arctan\frac{y}{x} + \pi\, u_0(-x)\, \operatorname{sgn} y$

$\begin{vmatrix}dx\\dy\\dz\end{vmatrix}= \begin{vmatrix} \sin\phi\cos\theta&\rho\cos\phi\cos\theta&-\rho\sin\phi\sin\theta\\ \sin\phi\sin\theta&\rho\cos\phi\sin\theta&\rho\sin\phi\cos\theta\\ \cos\phi&-\rho\sin\phi&0 \end{vmatrix}\cdot \begin{vmatrix}d\rho\\d\phi\\d\theta\end{vmatrix}$

$\begin{vmatrix}d\rho\\d\phi\\d\theta\end{vmatrix}= \begin{vmatrix} \frac{x}{\rho}&\frac{y}{\rho}&\frac{z}{\rho}\\ \frac{xz}{\rho^2\sqrt{x^2+y^2}}&\frac{yz}{\rho^2\sqrt{x^2+y^2}}&\frac{-(x^2+y^2)}{\rho^2\sqrt{x^2+y^2}}\\ \frac{-y}{x^2+y^2}&\frac{x}{x^2+y^2}&0 \end{vmatrix}\cdot \begin{vmatrix}dx\\dy\\dz\end{vmatrix}$

Цилиндрические и сферические

${r}=\rho \,\sin\phi$

${\theta}=\theta \quad$

${h}=\rho \,\cos\phi$

${\rho}=\sqrt{r^2+h^2}$

${\phi} =\arctan\frac{h}{r} + \pi \, u_0(-r) \, \operatorname{sgn} h$

${\theta}=\theta \quad$

$\begin{vmatrix}dr\\d\theta\\dh\end{vmatrix}= \begin{vmatrix} \sin\phi&\rho\cos\phi&0\\ 0&0&1\\ \cos\phi&-\rho\sin\phi&0 \end{vmatrix}\cdot \begin{vmatrix}d\rho\\d\phi\\d\theta\end{vmatrix}$

$\begin{vmatrix}d\rho\\d\phi\\d\theta\end{vmatrix}= \begin{vmatrix} \frac{r}{\sqrt{r^2+h^2}}&0&\frac{h}{\sqrt{r^2+h^2}}\\ \frac{-h}{r^2+h^2}&0&\frac{r}{r^2+h^2}\\ 0&1&0 \end{vmatrix}\cdot \begin{vmatrix}dr\\d\theta\\dh\end{vmatrix}$

См. также

• Системы координат в элементарной математике
• Галилеевы координаты
• Гауссовы координаты
• Нормальные координаты
• Римановы координаты
• Начало координат, координатная ось, орт
• Локальный стандарт покоя (начало координат в астрономии)
• Главноортодромическая система координат
• Размерность пространства

Литература

• Гельфанд И. М., Глаголева Е. Г., Кириллов А. А. Метод координат. Издание пятое, стереотипное. Серия: Библиотечка физико-математической школы. Математика. Выпуск 1. М.: Наука, 1973.

Ссылки

• Факультативное занятие по математике на тему: «Разные системы координат»