- Параболические координаты
-
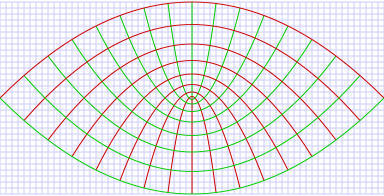
Параболические координаты — ортогональная система координат на плоскости, в которой координатные линии являются конфокальными параболами. Трёхмерный вариант этой системы координат получается при вращении парабол вокруг их оси симметрии.
Параболические координаты нашли многочисленные применения в математической физике, в частности, в теории эффекта Штарка и задаче о потенциале вблизи угла.
Содержание
Двумерные параболические координаты
Двумерные параболические координаты
 определяются выражениями
определяются выражениями
Поверхности постоянной
 являются конфокальными параболами
являются конфокальными параболамирасширяющимися вверх (вдоль луча
 ), а поверхности постоянной
), а поверхности постоянной  — это конфокальные параболы
— это конфокальные параболырасширяющиеся вниз (вдоль луча
 ). Фокусы всех парабол расположены в начале коорднат.
). Фокусы всех парабол расположены в начале коорднат.Дифференциальные характеристики двумерных координат
Коэффициенты Ламэ для параболических координат равны
Таким образом, элемент площади равен
а лапласиан равен
Прочие дифференциальные операторы могут быть аналогично найдены подстановкой коэффициентов Ламэ в соответствующую общую формулу.
Трёхмерные параболические координаты
На основе двумерных параболических координат строятся два типа трёхмерных координат. Первые получаются простым проектированием на плоскость
 вдоль оси
вдоль оси  и называются цилиндрические параболические координаты.
и называются цилиндрические параболические координаты.Вторая система координат, также называемая «параболические координаты», строится на основе параболоидов вращения, получаемых вращением парабол вокруг их оси симметрии
Ось параболоидов совпадает с осью
 , так как вокруг неё производится вращение. Азимутальный угол
, так как вокруг неё производится вращение. Азимутальный угол  определяется как
определяется какПоверхности постоянной
 являются конфокальными параболоидами
являются конфокальными параболоидаминаправленными вверх (вдоль луча
 ), а поверхности постоянной
), а поверхности постоянной  — это конфокальные параболоиды
— это конфокальные параболоидынаправленные вниз (вдоль луча
 ). Фокусы всех параболоидов расположены в начале координат.
). Фокусы всех параболоидов расположены в начале координат.Дифференциальные характеристики трёхмерных координат
Коэффициенты Ламэ в трёхмерном случае:
Как видно, коэффициенты
 и
и  совпадают с двумерным случаем. Элемент объёма равен
совпадают с двумерным случаем. Элемент объёма равена лапласиан равен
Прочие дифференциальные операторы, такие как дивергенция или ротор могут быть аналогично найдены подстановкой коэффициентов Ламэ в соответствующую общую формулу.
Обратные преобразования
Переход от декартовых координат
 к параболическим
к параболическим  осуществляется по формулам:
осуществляется по формулам:при этом

При
 получаем ограничение координат на плоскость
получаем ограничение координат на плоскость  :
:Линия уровня
 :
:Это парабола, фокус которой при любом
 расположен в начале координат.
расположен в начале координат.Аналогично при
 получаем
получаемКоординатные параболы пересекаются в точке
Пара парабол пересекается в двух точках, но при
 точка оказывается заключена в полуплоскости
точка оказывается заключена в полуплоскости  , так как
, так как  соответствует
соответствует  .
.Найдём коэффициенты наклоны касательных к параболам в точке
 :
:Так как произведение коэффициентов равно −1, то параболы перпендикулярны в точке пересечения. Таким образом, параболические координаты оказываются ортогональными.
Пара
 определяет координаты в полуплоскости. При изменении
определяет координаты в полуплоскости. При изменении  от 0 до
от 0 до  полуплоскость вращается вокруг оси
полуплоскость вращается вокруг оси  , в качестве координатных поверхностей получются параболоиды вращения и полуплоскости. Пара противоположных параболоидов определяет круг, а величина
, в качестве координатных поверхностей получются параболоиды вращения и полуплоскости. Пара противоположных параболоидов определяет круг, а величина  определяет полуплоскость, пересекающую круг в единственной точке. Её декартовы координаты равны:
определяет полуплоскость, пересекающую круг в единственной точке. Её декартовы координаты равны:Внешние ссылки
Weisstein, Eric W. Parabolic Coordinates (англ.) на сайте Wolfram MathWorld.
Категория:- Системы координат
Wikimedia Foundation. 2010.






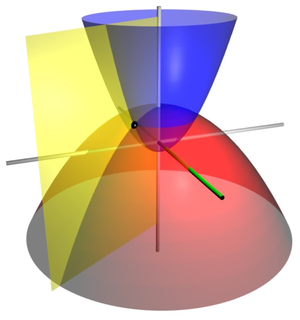
 , синий параболоид соответствует
, синий параболоид соответствует  , а жёлтая полуплоскость соответствует
, а жёлтая полуплоскость соответствует  . Три поверхности пересекаются в точке
. Три поверхности пересекаются в точке  (отмеченной чёрной сферой), имеющей декартовы координаты приблизительно
(отмеченной чёрной сферой), имеющей декартовы координаты приблизительно  .
.







![\nabla^2\Phi=\frac{1}{\sigma^2+\tau^2}\left[\frac{1}{\sigma}\frac{\partial}{\partial\sigma}\left(\sigma\frac{\partial\Phi}{\partial\sigma} \right)+\frac{1}{\tau}\frac{\partial}{\partial\tau}\left(\tau\frac{\partial\Phi}{\partial\tau}\right)\right]+\frac{1}{\sigma^2\tau^2}\frac{\partial^2\Phi}{\partial\varphi^2}.](8801708b285cf110d7b130f9522d1cb4.png)












 -мерные координаты
-мерные координаты