ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
- ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
поверхности - квадратичная форма от дифференциалов координат на поверхности, к-рая характеризует локальную структуру поверхности в окрестности обыкновенной точки. Пусть поверхность задана уравнением
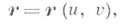
где  и
и  - внутренние координаты на поверхности;
- внутренние координаты на поверхности;
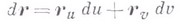
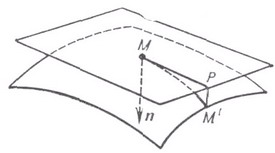
- дифференциал радиус-вектора 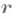 вдоль выбранного направления
вдоль выбранного направления  смещения из точки Мв точку М' (см. рис.);
смещения из точки Мв точку М' (см. рис.);
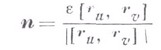
- единичный вектор нормали к поверхности в точке М(здесь  , если тройка векторов
, если тройка векторов  правой ориентации, и
правой ориентации, и 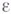 = - 1 в противоположном случае). Удвоенная главная линейная часть
= - 1 в противоположном случае). Удвоенная главная линейная часть 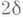 отклонения
отклонения  точки М' поверхности от касательной плоскости в ее точке Мравна
точки М' поверхности от касательной плоскости в ее точке Мравна
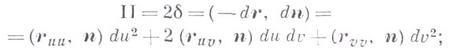
она и наз. второй основной квадратичной формой поверхности.
Коэффициенты В. к. ф. обычно обозначают через

или в тензорных символах
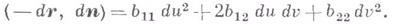
Тензор  наз. вторым основным тензором поверхности.
наз. вторым основным тензором поверхности.
О связи В. к. ф. с другими квадратичными формами поверхности и лит. см. Квадратичные формы поверхности. А. Б. Иванов.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА" в других словарях:
Вторая квадратичная форма — мерной поверхности, вложенной в пространство , квадратичная форма, задающая нормальную кривизну. Пусть нормальный вектор в точке , а локальная карта поверхности в точке . Тогда вторая квадратичная форма вычисляется по формуле … Википедия
Вторая фундаментальная форма — Вторая квадратичная форма n мерной поверхности, вложенной в пространство , квадратичная форма, задающая нормальную кривизну. Пусть нормальный вектор в точке P, а локальная карта поверхности в точке P. Тогда вторая квадратичная форма вычисляется… … Википедия
Первая квадратичная форма — или метрический тензор поверхности ― квадратичная форма от дифференциалов координат на поверхности, которая определяет внутреннюю геометрию поверхности в окрестности данной точки. Знание первой квадратичной формы достаточно для вычисления длин… … Википедия
Форма — I Форма (лат. forma – форма, вид, образ) 1) очертания, внешний вид, контуры предмета. 2) Внешнее выражение какого либо содержания (см. Содержание и форма). 3) Приспособление для придания чему либо определённых очертаний (например,… … Большая советская энциклопедия
НОРМАЛЬНАЯ ФОРМА — 1) Н. ф. матрицы A матрица Nзаранее определенного специального вида, получаемая из Ас помощью преобразований определенного типа. В зависимости от рассматриваемого типа преобразований, от области K, к к рой принадлежат коэффициенты А , от вида Аи … Математическая энциклопедия
КВАДРАТИЧНЫЕ ФОРМЫ ПОВЕРХНОСТИ — общее наименование квадратичных форм от дифференциалов координат на поверхности, инвариантных при преобразованиях этих координат. К. ф. п. характеризуют основные внутренние свойства поверхности и ее расположение в пространстве в окрестности… … Математическая энциклопедия
ГАУССОВА КРИВИЗНА — полная кривизна, поверхности произведение главных кривизн регулярной поверхности в данной точке. Если первая квадратичная форма поверхности и вторая квадратичная форма поверхности, то Г. к. вычисляется по формуле Г. к. совпадает с якобианом… … Математическая энциклопедия
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в к ром изучаются геометрич. образы, в первую очередь кривые и поверхности, методами математич. анализа. Обычно в Д. г. изучаются свойства кривых и поверхностей в малом, т. е. свойства сколь угодно малых их кусков. Кроме того, в … Математическая энциклопедия
Псевдосфера — (поверхность Бельтрами) поверхность постоянной отрицательной кривизны, образуемая вращением трактрисы около её асимптоты. Название п … Википедия
Точка округления — (круговая точка, омбилическая точка или омбилика; название «омбилика» происходит от лат. «umbilicus» ― «пуп») ― точка на гладкой регулярной поверхности в евклидовом пространстве, в которой нормальные кривизны по всем направлениям равны.… … Википедия
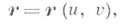
 и
и  - внутренние координаты на поверхности;
- внутренние координаты на поверхности;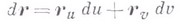
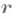 вдоль выбранного направления
вдоль выбранного направления  смещения из точки Мв точку М' (см. рис.);
смещения из точки Мв точку М' (см. рис.);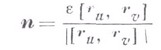
 , если тройка векторов
, если тройка векторов  правой ориентации, и
правой ориентации, и 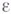 = - 1 в противоположном случае). Удвоенная главная линейная часть
= - 1 в противоположном случае). Удвоенная главная линейная часть 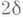 отклонения
отклонения  точки М' поверхности от касательной плоскости в ее точке Мравна
точки М' поверхности от касательной плоскости в ее точке Мравна 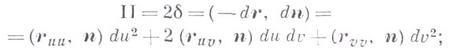

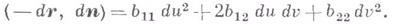
 наз. вторым основным тензором поверхности.
наз. вторым основным тензором поверхности.
