- НОРМАЛЬНАЯ ФОРМА
- 1) Н. ф. матрицы A - матрица Nзаранее определенного специального вида, получаемая из Ас помощью преобразований определенного типа. В зависимости от рассматриваемого типа преобразований, от области K, к к-рой принадлежат коэффициенты А , от вида Аи, наконец, от специфики решаемой задачи (напр., от желания расширять или не расширять Kпри переходе от Ак N, от необходимости определить N по А однозначно пли, наоборот, с нек-рым произволом) рассматриваются и различные Н. ф. Часто вместо термина "Н. ф." употребляют термины "каноническая форма", "канонический вид". К числу классических Н. ф. относятся следующие (ниже через
 обозначается множество всех матриц из тстрок и пстолбцов с коэффициентами из K).
обозначается множество всех матриц из тстрок и пстолбцов с коэффициентами из K).Нормальная форма Смита. Пусть K- либо кольцо
 целых рациональных чисел, либо кольцо
целых рациональных чисел, либо кольцо  многочленов от
многочленов от 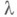 с коэффициентами из поля F. Матрица
с коэффициентами из поля F. Матрица  наз. эквивалентной матрице
наз. эквивалентной матрице  , если найдутся такие обратимые матрицы
, если найдутся такие обратимые матрицы  и
и 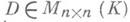 , что .
, что . . Матрица . Вэквивалентна А тогда и только тогда, когда Вможет быть получена из Ас помощью последовательности элементарных строчных и столбцовых преобразований, т. е. преобразований следующих трех типов: а) перестановка строк (столбцов); б) прибавление к одной строке (столбцу) другой строки (столбца) с множителем из K;в). умножение строки (столбца) на обратимый элемент кольца K. Для преобразований этого типа справедливо следующее утверждение: всякая матрица
. Матрица . Вэквивалентна А тогда и только тогда, когда Вможет быть получена из Ас помощью последовательности элементарных строчных и столбцовых преобразований, т. е. преобразований следующих трех типов: а) перестановка строк (столбцов); б) прибавление к одной строке (столбцу) другой строки (столбца) с множителем из K;в). умножение строки (столбца) на обратимый элемент кольца K. Для преобразований этого типа справедливо следующее утверждение: всякая матрица  эквивалентна матрице
эквивалентна матрице  вида
вида 
где
 при всех
при всех  делит
делит  при
при  и если
и если  , то все
, то все  положительны, а если
положительны, а если 
 , то старшие коэффициенты всех многочленов
, то старшие коэффициенты всех многочленов  равны 1. Указанная матрица Nназ. нормальной формой Смита матрицы А. Элементы
равны 1. Указанная матрица Nназ. нормальной формой Смита матрицы А. Элементы  наз. инвариантными множителями матрицы А, а число r- ее рангом. Нормальная форма Смита определена по Аоднозначно и может быть найдена следующим образом. Ранг Аравен порядку наименьшего ненулевого минора матрицы А. Пусть
наз. инвариантными множителями матрицы А, а число r- ее рангом. Нормальная форма Смита определена по Аоднозначно и может быть найдена следующим образом. Ранг Аравен порядку наименьшего ненулевого минора матрицы А. Пусть  ; тогда среди всех миноров порядка
; тогда среди всех миноров порядка 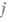 матрицы Аимеется хоть один ненулевой. Пусть
матрицы Аимеется хоть один ненулевой. Пусть 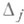 ,
,  - наибольший общий делитель всех ненулевых миноров порядка jматрицы А(нормированный условием, что
- наибольший общий делитель всех ненулевых миноров порядка jматрицы А(нормированный условием, что  при
при  и что старший коэффициент многочлена
и что старший коэффициент многочлена 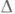 j равен 1 при
j равен 1 при  ) и пусть
) и пусть 
 . Тогда
. Тогда  Инвариантные множители являются полным набором инвариантов классов эквивалентных матриц: две матрицы из
Инвариантные множители являются полным набором инвариантов классов эквивалентных матриц: две матрицы из 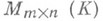 эквивалентны тогда и только тогда, когда у них совпадают ранги и инвариантные множители с равными номерами.
эквивалентны тогда и только тогда, когда у них совпадают ранги и инвариантные множители с равными номерами.Инвариантные множители
 раскладываются (единственным способом с точностью до порядка сомножителей) в произведение степеней неприводимых в кольце К элементов
раскладываются (единственным способом с точностью до порядка сомножителей) в произведение степеней неприводимых в кольце К элементов  (являющихся нек-рыми целыми положительными числами, большими 1, если
(являющихся нек-рыми целыми положительными числами, большими 1, если  , и нек-рыми многочленами положительной степени со старшим коэффициентом 1, если
, и нек-рыми многочленами положительной степени со старшим коэффициентом 1, если  ),
), 
где
 - целые неотрицательные числа. Каждый множитель
- целые неотрицательные числа. Каждый множитель  , для к-рого
, для к-рого  , наз. элементарным делителем матрицы А(над К). Каждый элементарный делитель входит в совокупность
, наз. элементарным делителем матрицы А(над К). Каждый элементарный делитель входит в совокупность  всех элементарных делителей матрицы Астолько раз, в разложении скольких инвариантных множителей он встречается. Элементарные делители, в отличие от инвариантных множителей, зависят от того, над каким кольцом Крассматривается А: если
всех элементарных делителей матрицы Астолько раз, в разложении скольких инвариантных множителей он встречается. Элементарные делители, в отличие от инвариантных множителей, зависят от того, над каким кольцом Крассматривается А: если 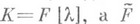 - нек-рое расширение поля
- нек-рое расширение поля  то матрица
то матрица имеет, вообще говоря, различные элементарные делители (но одинаковые инвариантные множители) в зависимости от того, рассматривается ли A как элемент
имеет, вообще говоря, различные элементарные делители (но одинаковые инвариантные множители) в зависимости от того, рассматривается ли A как элемент  или как элемент
или как элемент  . Инвариантные множители восстанавливаются по полному набору элементарных делителей и наоборот.
. Инвариантные множители восстанавливаются по полному набору элементарных делителей и наоборот.Практический способ нахождения нормальной формы Смита см., напр., в [1].
Указанный основной результат о нормальной форме Смита получен для
 (см. [71), для
(см. [71), для  (см.[8]). Практически без изменений теория нормальных форм Смита переносится на случай, когда К- любое кольцо главных идеалов (см. [3], [6]). Нормальная форма Смита имеет важные приложения, напр, на ней по существу основывается структурная теория конечно порожденных модулей над кольцами главных идеалов (см. [3], [6]) и, в частности, теория конечно порожденных абелевых групп и теория жордановой Н. ф. (см. ниже).
(см.[8]). Практически без изменений теория нормальных форм Смита переносится на случай, когда К- любое кольцо главных идеалов (см. [3], [6]). Нормальная форма Смита имеет важные приложения, напр, на ней по существу основывается структурная теория конечно порожденных модулей над кольцами главных идеалов (см. [3], [6]) и, в частности, теория конечно порожденных абелевых групп и теория жордановой Н. ф. (см. ниже).Естественная нормальная форма. Пусть К- поле. Две квадратные матрицы
 и
и 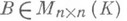 наз. подобными над К, если найдется такая невырожденная матрица
наз. подобными над К, если найдется такая невырожденная матрица 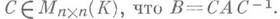 Имеется тесная связь между подобием и эквивалентностью: матрицы .
Имеется тесная связь между подобием и эквивалентностью: матрицы . подобны тогда и только тогда, когда матрицы
подобны тогда и только тогда, когда матрицы  , где Е- единичная матрица, эквивалентны. Таким образом, для подобия Аи Внеобходимо и достаточно совпадения инвариантных множителей или, что то же,- наборов элементарных делителей над
, где Е- единичная матрица, эквивалентны. Таким образом, для подобия Аи Внеобходимо и достаточно совпадения инвариантных множителей или, что то же,- наборов элементарных делителей над  у матриц
у матриц  Практический способ нахождения матрицы Сдля подобных матриц Аи Всм. в [1], [4].
Практический способ нахождения матрицы Сдля подобных матриц Аи Всм. в [1], [4].Матрица
 наз. характеристической матрицей матрицы
наз. характеристической матрицей матрицы  а инвариантные множители
а инвариантные множители  наз. инвариантами подобия матрицы А; их пштук. Пусть
наз. инвариантами подобия матрицы А; их пштук. Пусть  - инварианты подобия матрицы А. Многочлен
- инварианты подобия матрицы А. Многочлен  равен определителю матрицы
равен определителю матрицы  и наз. характеристическим многочленом матрицы А. Пусть
и наз. характеристическим многочленом матрицы А. Пусть  а степень
а степень 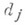 при
при  больше 1.
больше 1.Тогда справедливо утверждение: матрица Аподобна над Кблочнодиагональной матрице
 вида
вида
где через
 для многочлена
для многочлена
обозначена т. н. сопровождающая матрица многочлена

Матрица
 определена по Аоднозначно и наз. первой естественной Н. ф. матрицы А(см. [1], [2]).
определена по Аоднозначно и наз. первой естественной Н. ф. матрицы А(см. [1], [2]).Пусть теперь
 - набор всех элементарных делителей матрицы
- набор всех элементарных делителей матрицы  . Тогда справедливо следующее основное утверждение: матрица Аподобна над Кблочнодиагональной матрице N2, блоки к-рой - это сопровождающие матрицы всевозможных элементарных делителей
. Тогда справедливо следующее основное утверждение: матрица Аподобна над Кблочнодиагональной матрице N2, блоки к-рой - это сопровождающие матрицы всевозможных элементарных делителей  матрицы
матрицы  :
:
Матрица
 определена по Алишь с точностью до порядка следования клеток по главной диагонали; она наз. второй естественной Н. ф. матрицы А(см. [1], [2]), а также еефробениусовой, рациональной, канонической и квазиестественной Н. ф. (см. [4]). В отличие от первой естественной Н. ф., вторая естественная Н. ф., вообще говоря, меняется при переходе от поля Кк его расширению.
определена по Алишь с точностью до порядка следования клеток по главной диагонали; она наз. второй естественной Н. ф. матрицы А(см. [1], [2]), а также еефробениусовой, рациональной, канонической и квазиестественной Н. ф. (см. [4]). В отличие от первой естественной Н. ф., вторая естественная Н. ф., вообще говоря, меняется при переходе от поля Кк его расширению.Жорданова нормальная форма. Пусть К - поле,
 - набор всех элементарных делителей матрицы
- набор всех элементарных делителей матрицы  над
над  . Пусть Кобладает тем свойством, что характеристич. многочлен dn матрицы Араскладывается в
. Пусть Кобладает тем свойством, что характеристич. многочлен dn матрицы Араскладывается в  на линейные множители (так будет, напр., если К- поле комплексных чисел или, более общо, любое алгебраически замкнутое поле). Тогда каждый из многочленов
на линейные множители (так будет, напр., если К- поле комплексных чисел или, более общо, любое алгебраически замкнутое поле). Тогда каждый из многочленов  имеет вид
имеет вид  для нек-рого
для нек-рого  , а элементарный делитель
, а элементарный делитель  соответственно имеет вид
соответственно имеет вид  . Матрица
. Матрица  иа
иа  вида
вида  где
где  наз. г пперсопровождающей матрицей многочлена f (см. [1]), или жордановой клеткой порядка s с собственным числом а. Справедливо следующее фундаментальное утверждение: матрица Аподобна над Кблочнодиагональной матрице
наз. г пперсопровождающей матрицей многочлена f (см. [1]), или жордановой клеткой порядка s с собственным числом а. Справедливо следующее фундаментальное утверждение: матрица Аподобна над Кблочнодиагональной матрице  блоки к-рой - это гиперсопровождающие матрицы всевозможных элементарных делителей матрицы
блоки к-рой - это гиперсопровождающие матрицы всевозможных элементарных делителей матрицы 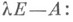

Матрица J определена лишь с точностью до порядка следования клеток на главной диагонали; она является жордановой матрицей и наз. жордановой Н. ф. матрицы А. Если Кне обладает указанным выше свойством, то Анельзя привести над Кк жордановой Н. ф. (но можно над нек-рым конечным расширением К). О так наз. обобщенной жордановой Н. ф., приведение к к-рой возможно уже над любым полем К, см. [4]. Помимо различных теорий Н. ф. для произвольных матриц возможны соответствующие теории и для матриц какого-либо специального вида. Классическими примерами являются теории Н. ф. симметрия, и косо-симметрич. матриц. А именно, пусть К- поле. Две матрицы
 наз. конгруэнтными (см. [1]), если найдется такая невырожденная матрица
наз. конгруэнтными (см. [1]), если найдется такая невырожденная матрица 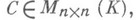 что
что  Н. ф. относительно отношения конгруэнтности наиболее исследованы для классов симметрич. и кососимметрич. матриц. Пусть
Н. ф. относительно отношения конгруэнтности наиболее исследованы для классов симметрич. и кососимметрич. матриц. Пусть  и А- кососимметрич. матрица, т. е.
и А- кососимметрич. матрица, т. е.  . Тогда Аконгруэнтна однозначно определенной матрице H вида
. Тогда Аконгруэнтна однозначно определенной матрице H вида
к-рая может рассматриваться как Н. ф. Аотносительно отношения конгруэнтности. Если же А- симметрич. матрица, т. е.
 то она конгруэнтна матрице Dвида
то она конгруэнтна матрице Dвида
где
 при всех i. Число r равно рангу Аи определено однозначно, а дальнейшее уточнение выбора элементов ei зависит от свойств поля К. Так, если Калгебраически замкнуто, то можно считать, что
при всех i. Число r равно рангу Аи определено однозначно, а дальнейшее уточнение выбора элементов ei зависит от свойств поля К. Так, если Калгебраически замкнуто, то можно считать, что 
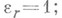 если К- поле действительных чисел, то можно считать, что
если К- поле действительных чисел, то можно считать, что  для нек-рого р. Этими свойствами Dуже определена однозначно и может рассматриваться как Н. ф. Аотносительно отношения конгруэнтности. О Н. ф. симметрич. матриц для ряда других полей, а также об эрмитовых аналогах этой теории см. [6], [10] и ст. Квадратичная ферма.
для нек-рого р. Этими свойствами Dуже определена однозначно и может рассматриваться как Н. ф. Аотносительно отношения конгруэнтности. О Н. ф. симметрич. матриц для ряда других полей, а также об эрмитовых аналогах этой теории см. [6], [10] и ст. Квадратичная ферма.Объединяющим обстоятельством в рассмотренных (а также и других) теориях Н. ф. является то, что допустимые преобразования над рассматриваемым множеством матриц определяются действием нек-рой группы, так что классы матриц, переводимых друг в друга с помощью этих преобразований,- орбиты этой группы, а указание Н. ф. есть выделение в каждой орбите нек-рого канонич. представителя. Так, классы эквивалентных матриц - орбиты группы
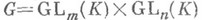 (где
(где  - группы обратимых квадратных матриц порядка sс коэффициентами из К), действующей на
- группы обратимых квадратных матриц порядка sс коэффициентами из К), действующей на  по правилу где
по правилу где 
 . Классы подобных матриц - это орбиты группы
. Классы подобных матриц - это орбиты группы  на
на  действующей по правилу:
действующей по правилу: Классы конгруэнтных симметрич. или кососимметрич. матриц - это орбиты группы GLn(K)на множестве всех симметрич. или кососимметрич. матриц порядка п, действующей по правилу
Классы конгруэнтных симметрич. или кососимметрич. матриц - это орбиты группы GLn(K)на множестве всех симметрич. или кососимметрич. матриц порядка п, действующей по правилу  где
где  С этой точки зрения каждая теория Н. ф. является конкретным примером решения части общей задачи орбитального разложения для действия нек-рой группы преобразований.
С этой точки зрения каждая теория Н. ф. является конкретным примером решения части общей задачи орбитального разложения для действия нек-рой группы преобразований.Лит.:[1] Маркус М., Минк X., Обзор по теории матриц и матричных неравенств, пер. с англ., М., 1972; [2] Ланкастер П., Теория матриц, пер. с англ., М., 1978; [3] Ленг С, Алгебра, пер. с англ., М., 1968; [4] Мальцев А. И., Основы линейной алгебры, 4 изд., М., 1975: [5] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962; [6] Бурбаки Н., Алгебра. Модули, кольца, формы, пер. с франц., М., 1966; [7] Smith H. J., The Collected Mathematical Paper, v. 1, Oxf., 1894, p. 367-409; [8] Frоbenius G., "J. reine und angew. Math.", 1879, Bd 86, S. 146-208; [9] Гантмахер Ф. Р., Теория матриц, 2 изд., М., 1966; [10] Серр Ж.-П., Курс арифметики, пер. с франц., М., 1972.
В. Л. Попов.
2) Н. ф. оператора - представление с точностью до изоморфизма самосопряженного оператора А, действующего в гильбертовом пространстве
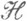 , в виде ортогональной суммы операторов умножения на независимую переменную.
, в виде ортогональной суммы операторов умножения на независимую переменную.Пусть, сначала, А- циклический оператор; это означает, что существует элемент
 такой, что любой элемент
такой, что любой элемент  однозначйо представим в виде
однозначйо представим в виде  - нек-рая функция такая, что
- нек-рая функция такая, что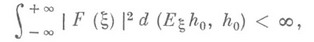
здесь
 - спектральная функция оператора А. Пусть
- спектральная функция оператора А. Пусть  - пространство функций, суммируемых с квадратом на
- пространство функций, суммируемых с квадратом на 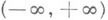 с весом
с весом  и
и  - оператор умножения на независимую переменную с областью определения
- оператор умножения на независимую переменную с областью определения
Тогда операторы Аи Кизоморфны,
 , т. е. существует изоморфное и изометрич. отображение
, т. е. существует изоморфное и изометрич. отображение 
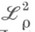 такое, что
такое, что 
Пусть, теперь, А - произвольный самосопряженный оператор. Тогда Нможно разложить в ортогональную сумму инвариантных подпространств
 , на каждом из к-рых Аиндуцирует циклич. операторы
, на каждом из к-рых Аиндуцирует циклич. операторы 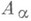 , так что
, так что  Если на
Если на 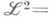
 задать оператор
задать оператор  то
то 
Оператор Кназ. нормальной формой, пли каноническим представлением, оператора А. Теорема о канонич. представлении распространяется на случай произвольных нормальных операторов.
Лит.:[l] Плеснер А. И., Спектральная теория линейных операторов, М., 1965; [2] Ахиезер Н. И., Глазпан И. М., Теория линейных операторов в гильбертовом пространстве, 2 изд., М., 1966.
В. И. Соболев.
3) Н. ф. оператора - представление оператора А, действующего в Фока пространстве, построенном над нек-рым пространством
 где
где 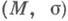 - пространство с мерой, в виде суммы
- пространство с мерой, в виде суммы
где
 - операторнозначные обобщенные функции, порождающие семейства операторов уничтожения
- операторнозначные обобщенные функции, порождающие семейства операторов уничтожения  и рождения
и рождения 


В выражении (1) в каждом слагаемом множители a(yj), j = 1, ..., т, стоят правее всех множителей а*( х i), i=1,..., п, функции (возможно обобщенные) К п , т( х 1 , ..., х п ; y1, ..., у т )от двух наборов переменных ( х 1 , ...,х п)
 М n, ( у 1 ,..., у т )
М n, ( у 1 ,..., у т ) М т, n, m=0, 1,2, ..., в случае симметричного (бозонного) пространства Фока симметричны по переменным каждого из наборов в отдельности, а в случае антисимметричного (фермионного) пространства Фока - антисимметричны по этим переменным.
М т, n, m=0, 1,2, ..., в случае симметричного (бозонного) пространства Фока симметричны по переменным каждого из наборов в отдельности, а в случае антисимметричного (фермионного) пространства Фока - антисимметричны по этим переменным.Для любого ограниченного оператора Анормальная форма существует и единственна.
Представление (1) можно переписать в виде, непосредственно содержащем операторы уничтожения и рождения:

где
 - нек-рый ортонормированный базис в
- нек-рый ортонормированный базис в  , и суммирование в (2) происходит
, и суммирование в (2) происходитпо всем парам конечных наборов

 элементов этого базиса.
элементов этого базиса.В случае произвольного (сепарабельного) гильбертова пространства НН. ф. оператора А, действующего в пространстве Фока Г (H), построенном над H, определяется при фиксированном базисе
 в Нс помощью выражения (2), где
в Нс помощью выражения (2), где 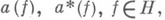 - семейства операторов уничтожения и рождения, действующих в Г (H).
- семейства операторов уничтожения и рождения, действующих в Г (H).Лит.:[1] Березин Ф. А., Метод вторичного квантования, М., 1965.
Р. А. Миплос.
4) Н. ф. рекурсивной функции - способ задания n-местной рекурсивной функции j в виде

где f есть (n+1)-местная примитивно рекурсивная функция, g- одноместная примитивно рекурсивная функция,
 - результат применения наименьшего числа оператора к функции f. Теорема Клини о Н. ф. утверждает: существует такая примитивно рекурсивная функция g, что каждая рекурсивная функция
- результат применения наименьшего числа оператора к функции f. Теорема Клини о Н. ф. утверждает: существует такая примитивно рекурсивная функция g, что каждая рекурсивная функция  представима в виде (*) с подходящей функцией f, зависящей от
представима в виде (*) с подходящей функцией f, зависящей от  , т. е.
, т. е.
Теорема о Н. ф. является одной из важнейших теорем в теории рекурсивных функций.
А. А. Марков [2] получил характеристику тех функций g, к-рые могут использоваться в теореме о Н. ф. в представлении (*). Функция gтогда и только тогда может использоваться в качестве функции, существование к-рой утверждается в теореме о Н. ф., когда уравнение g(x)= ппри любом пимеет бесконечно много решений. Такие функции наз. функциями большого размаха.
Лит.:[l] Мальцев А. И., Алгоритмы и рекурсивные функции, М., 1965; [2] Марков А. А., "Изв. АН СССР. Сер. матем.", 1949, т. 13, № 5, с. 417-24.
В. Е. Плиско.
5) Н. ф. системы дифференциальных уравнений

вблизи инвариантного многообразия М- такая формальная система

к-рая получается из (1) обратимой формальной заменой координат

и в к-рой ряды Тейлора - Фурье yi содержат только резонансные члены. Впервые Н. ф. для одного случая встречается в диссертации А. Пуанкаре (Н. Poincare, см. [1]). Посредством Н. ф. (2) нек-рые системы (1) интегрируются, многие исследуются на устойчивость и интегрируются приближенно, для систем (1) отыскиваются периодич. решения и семейства условно перио-дич. решений, изучаются их бифуркации.
Н. ф. в окрестности неподвижной точки. Пусть М- неподвижная точка
 системы (1) (т. е.
системы (1) (т. е.  ), функции
), функции 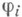 аналитичны в ней и
аналитичны в ней и 
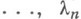 - собственные значения матрицы
- собственные значения матрицы  при X= 0. Пусть
при X= 0. Пусть  Тогда в полной окрестности точки X =0 система (1) имеет следующую Н. ф. (2): матрица
Тогда в полной окрестности точки X =0 система (1) имеет следующую Н. ф. (2): матрица  при
при 
 имеет Н. ф. (напр., жорданову), а ряды Тейлора
имеет Н. ф. (напр., жорданову), а ряды Тейлора 
содержат только резонансные члены, для к-рых

Если уравнение (5) не имеет в
 решений
решений  то Н. ф. (2) является линейной:
то Н. ф. (2) является линейной:
Всякая система (1) с
 в окрестности неподвижной точки приводится к своей Н. ф. (2) нек-рым формальным преобразованием (3), где
в окрестности неподвижной точки приводится к своей Н. ф. (2) нек-рым формальным преобразованием (3), где  - степенные ряды (возможно, расходящиеся),
- степенные ряды (возможно, расходящиеся),  и
и  при Y = 0.
при Y = 0.Вообще говоря, нормализующее преобразование (3)и Н. ф. (2) (т. е. коэффициенты
 в (4)) неоднозначно определяются исходной системой (1). Н. ф. (2) сохраняет мпогие свойства системы (1): вещественность, симметричность, гамильтоновость и др. (см. [2], [3]). Если в исходной системе имеются малые параметры, то их можно включить в число координат
в (4)) неоднозначно определяются исходной системой (1). Н. ф. (2) сохраняет мпогие свойства системы (1): вещественность, симметричность, гамильтоновость и др. (см. [2], [3]). Если в исходной системе имеются малые параметры, то их можно включить в число координат  , тогда
, тогда  При нормализующем преобразовании такие координаты не меняются (см. [3]).
При нормализующем преобразовании такие координаты не меняются (см. [3]).Если k- число линейно независимых решений
 уравнения (5), то с помощью преобразования
уравнения (5), то с помощью преобразования
где
 - целые иН. ф. (2) переводится
- целые иН. ф. (2) переводитсяв систему вида


(см. [2], [3]). Решение этой системы сводится к решению подсистемы из первых куравнений и к п-к квадратурам. Подсистему надо исследовать в окрестности сложной особой точки
 ибо
ибо  не содержат линейных членов. Это можно сделать с помощью локального метода (см. [3]).
не содержат линейных членов. Это можно сделать с помощью локального метода (см. [3]).Рассматривался вопрос (см. [2]): при каких условиях на Н. ф. (2) сходится (аналнтично) нормализующее преобразование аналитической системы (1)? Пусть

по таким
 для к-рых
для к-рых
в. Условие:


Условие
 :
:
Условие
 слабее условия w. Оба они выполнены для почти всех
слабее условия w. Оба они выполнены для почти всех  (по мере Лебега) и являются очень слабыми арифметич. ограничениями на
(по мере Лебега) и являются очень слабыми арифметич. ограничениями на  .
.Условие А в случае
 (общий случай см. в [2] ): существует такой степенной ряд
(общий случай см. в [2] ): существует такой степенной ряд  , что в (4)
, что в (4) Если аналитич. системы (1) Л удовлетворяет условию w и Н. ф. (2) удовлетворяет условию А, то существует аналитич. реобразование системы (1) к нек-рой Н. ф. Если Н. ф. (2) получается из нек-рой аналитич. системы и не удовлетворяет хотя бы одному из условий
Если аналитич. системы (1) Л удовлетворяет условию w и Н. ф. (2) удовлетворяет условию А, то существует аналитич. реобразование системы (1) к нек-рой Н. ф. Если Н. ф. (2) получается из нек-рой аналитич. системы и не удовлетворяет хотя бы одному из условий  и А, то существует такая аналитич. система (1), к-рая имеет (2) своей Н. ф. и всякое преобразование к-рой к Н. ф. расходится (не аналитично).
и А, то существует такая аналитич. система (1), к-рая имеет (2) своей Н. ф. и всякое преобразование к-рой к Н. ф. расходится (не аналитично).Таким образом, поставленный выше вопрос решен для всех Н. ф., кроме тех, у к-рых
 удовлетворяет условию
удовлетворяет условию  и не удовлетворяет условию
и не удовлетворяет условию  , а остальные коэффициенты Н. ф. удовлетворяют условию А. Условие А является очень жестким ограничением на коэффициенты Н. ф., и для больших поно выполнено, вообще говоря, только в вырожденных случаях. Т. <е. основная причина расходимости преобразований к Н. ф.- это не малые знаменатели, а невырожденность Н. ф.
, а остальные коэффициенты Н. ф. удовлетворяют условию А. Условие А является очень жестким ограничением на коэффициенты Н. ф., и для больших поно выполнено, вообще говоря, только в вырожденных случаях. Т. <е. основная причина расходимости преобразований к Н. ф.- это не малые знаменатели, а невырожденность Н. ф.Но и в случаях расходимости нормализующего преобразования (3) по Н. ф. (2) можно изучить свойства решений системы (1). Так, для вещественной системы (1) гладкое преобразование к Н. ф. (2) существует и в тех случаях, когда нет аналитического. Большинство результатов о гладкой нормализации получено при условии, что все
 При этом условии с помощью замены
При этом условии с помощью замены  конечного класса гладкости систему (1) можно привести к укороченной Н. ф.
конечного класса гладкости систему (1) можно привести к укороченной Н. ф.
где
 - многочлены степени т(см. [4] - [6]). Если в нормализующем преобразовании (3) отбросить все члены степени выше т, то получится преобразование
- многочлены степени т(см. [4] - [6]). Если в нормализующем преобразовании (3) отбросить все члены степени выше т, то получится преобразование
(
 - многочлены), к-рое приводит (1) к виду
- многочлены), к-рое приводит (1) к виду
где
 - многочлены, содержащие только резонансные члены,
- многочлены, содержащие только резонансные члены, - сходящиеся степенные ряды, содержащие только члены степени выше т. Решения укороченной Н. ф. (6) служат приближениями для решений системы (8) и после преобразования (7) дают приближения решений исходной системы (1). Во многих случаях для (6) удается построить такую Ляпунова функцию (или Четаева функцию) f(V), что
- сходящиеся степенные ряды, содержащие только члены степени выше т. Решения укороченной Н. ф. (6) служат приближениями для решений системы (8) и после преобразования (7) дают приближения решений исходной системы (1). Во многих случаях для (6) удается построить такую Ляпунова функцию (или Четаева функцию) f(V), что
где
 и
и  - положительные постоянные. Тогда f(U)будет функцией Ляпунова (Четаева для системы (8), т. е. точка X= 0 будет устойчивой (неустойчивой). Напр., если все
- положительные постоянные. Тогда f(U)будет функцией Ляпунова (Четаева для системы (8), т. е. точка X= 0 будет устойчивой (неустойчивой). Напр., если все  то можно взять т -1,
то можно взять т -1, 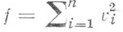 и получится теорема Ляпунова об устойчивости по линейному приближению (см. [7]; другие примеры см. в обзоре [8]).
и получится теорема Ляпунова об устойчивости по линейному приближению (см. [7]; другие примеры см. в обзоре [8]).По Н. ф. (2) можно находить инвариантные аналитические множества системы (1). В дальнейшем для простоты изложения предполагается, что Rе L= 0. По Н. ф. (2) выделяется формальное множество

где а- свободный параметр. На множестве
 выполняется условие А. Пусть К- объединение таких подпространств вида
выполняется условие А. Пусть К- объединение таких подпространств вида  что соответствующие собственные значения
что соответствующие собственные значения 
 попарно соизмеримы. Формальное множество
попарно соизмеримы. Формальное множество  аналитично в системе (1). Из
аналитично в системе (1). Из  выделяется подмножество
выделяется подмножество 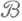 , к-рое аналитично в системе (1), если выполнено условие
, к-рое аналитично в системе (1), если выполнено условие  (см. [3]). На множествах
(см. [3]). На множествах 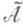 и
и  лежат периодич. решения и семейства условно перподич. решений системы (1). Рассматривая множества
лежат периодич. решения и семейства условно перподич. решений системы (1). Рассматривая множества  и
и  в системах с малыми параметрами, можно изучить все аналитич. возмущения и бифуркации таких решений (см. [9]).
в системах с малыми параметрами, можно изучить все аналитич. возмущения и бифуркации таких решений (см. [9]).Обобщения. Если систему (1) приводить не к Н. ф. (2), а к системе, правые части к-рой содержат нек-рые нерезонансные члены, то упрощение получается менее значительным, зато можно улучшить качество преобразования. Так, приведение к "полунормальной форме" будет аналитическим при ослабленном условии А (см. [2]). Другой вариант - преобразование, нормализующее систему (1) лишь на нек-рых подмногообразиях (напр., на нек-рых координатных подпространствах; см. [2]). Комбинации этих подходов позволяют доказать для системы (1) существование инвариантных подмногообразий и решений определенного вида (см. [9]).
Пусть система (1) определена и аналитична в окрестности инвариантного многообразия Мразмерности k+l, к-рое расслаивается на l-мерные инвариантные торы. Тогда вблизи Мможно ввести такие локальные координаты

что
 на
на  имеют период 2
имеют период 2  , Sпробегает нек-рую область Н, и система (1) принимает вид
, Sпробегает нек-рую область Н, и система (1) принимает вид
где
 А-матрица.
А-матрица.Если
 = const и матрица Атреугольна с постоянной главной диагональю
= const и матрица Атреугольна с постоянной главной диагональю  , то (при слабом ограничении на малые знаменатели) существует формальное преобразование локальных координат S, Y,
, то (при слабом ограничении на малые знаменатели) существует формальное преобразование локальных координат S, Y,  к-рое приводит систему (9) к Н. ф.
к-рое приводит систему (9) к Н. ф.
Если среди координат Z есть малый параметр, то систему (9) можно осреднить Крылова- Боголюбова методом усреднения (см. [10]), и осредненная система будет Н. ф. Вообще, теорию возмущений можно рассматривать как частный случай теории Н. ф., когда одна из координат является малым параметром (см. [11]).
На системы (9) и (10) переносятся теоремы о сходимости нормализующей замены, теоремы о существовании аналитических инвариантных множеств и т. д. Здесь наиболее изучен случай, когда М- периодич. решение, т. е. к= 0, l =1. В этом случае теория Н. ф. во многом идентична случаю, когда М- неподвижная точка. А. Пуанкаре предложил рассматривать точечное преобразование нормального сечения за период. В связи с этим возникла теория Н. ф. точечных отображений, к-рая параллельна соответствующей теории для систем (1). Другие обобщения Н. ф. см. в [3], [б], [12], [1З].
Лит.:[1] Пуанкаре А., Избр. труды, пер. с франц., т. 3, М., 1974; [2] Брюно А. Д., "Тр. Моск. матем. об-ва", 1971, т. 25, с. 119-262; 1972, т. 26, с. 199 - 239; [3] его же, Локальный метод нелинейного анализа дифференциальных уравнений, М., 1979; [4] Xартман Ф., Обыкновенные дифференциальные уравнения, пер. с англ., М., 1970; [5.1 Самовол В. С, "Докл. АН СССР", 1972, т. 206, № 3, с. 545 - 48; [6] Белицкий Г. Р., Нормальные формы, инварианты и локальные отображения. К., 1979; [7] Ляпунов А. М., Общая задача об устойчивости движения, 2 изд., М.- Л., 1935; [8] Куницын А. Л., Маркеев А. П., Итоги науки и техники. Сер. Общая механика, т. 4, М., 1979, с. 58-139; [9] Bibi'kov J. N.. Local theory of nonlinear analytic ordinary differential equations, В. [а. о.], 1979; [10] Боголюбов H. H., Митропольский Ю. А., Асимптотические методы в теории нелинейных колебаний, 4 изд., М., 1974; [11] Брюно А. Д., "Рrос. VIII Intern. Conf. on Nonlinear Oscillations", Prague, 1979, v. 1, p. 177-82; [12] Костiн В. В., Ле Дiнь Тхюi, "Доповiдi АН УРСР. Сер. А", 1975, № 11, с. 982-85; [13] Zehnder E. J., "Manus. math.", 1978, v. 23, p. 363-71.
А. Д. Брюно.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
