КРАЕВАЯ ЗАДАЧА — теории потенциала основная задача потенциала теории как классической, так и абстрактной. Поскольку классические ньютонов и логарифмич. потенциалы удовлетворяют определенным дифференциальным уравнениям с частными производными эллиптич. типа, а… … Математическая энциклопедия
Задача Неймана — Задача Неймана, вторая краевая задача в дифференциальных уравнениях краевая задача с заданными граничными условиями для производной искомой функции на границе области так называемые граничные условия второго рода. По типу области… … Википедия
Неймана задача — вторая краевая задача, одна из краевых задач (См. Краевые задачи), ставящихся для дифференциальных уравнений с частными производными второго порядка. В простейших случаях (в частности, для уравнения Лапласа) Н. з. состоит в отыскании… … Большая советская энциклопедия
НЕЙМАНА ЗАДАЧА — то же, что вторая краевая задача. Названа по имени К. Неймана (К. Neumann, 1877), к рый впервые систематически исследовал ее … Математическая энциклопедия
СМЕШАННАЯ И КРАЕВАЯ ЗАДАЧИ ДЛЯ ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ И СИСТЕМ — задачи отыскания решений и( х, t) = (u1(x, t),..., и т( х, t) в области Dевклидова пространства =(x1, . . ., х п, t) точка пространства ) параболич. системы уравнений или при m =1параболич. уравнения, удовлетворяющих нек рым дополнительным… … Математическая энциклопедия
ГАРМОНИЧЕСКАЯ ФУНКЦИЯ — действительная функция заданная в области Dевклидова пространства имеющая в Dнепрерывные частные производные 1 го и 2 го порядков и являющаяся решением Лапласа уравнения где декартовы прямоугольные координаты точки х. Иногда это определение… … Математическая энциклопедия
ЖИРО УСЛОВИЯ — условия разрешимости в классич. смысле основных краевых задач для линейного эллиптич. уравнения 2 го порядка. Пусть в ограниченной TV мерной области Dс границей Г задано эллиптич. уравнение Требуется найти функцию и(х), к рая: 1) принадлежит… … Математическая энциклопедия
ЛАПЛАСА УРАВНЕНИЕ — однородное дифференциальное уравнение с частными производными вида где функция от пдействительных переменных. Левая часть Л. у. наз. Лапласа оператором от функции и. Регулярные решения Л. у. класса С 2 в нек рой области Dевклидова пространства т … Математическая энциклопедия
ГАРМОНИЧЕСКАЯ ФУНКЦИЯ — функция, непрерывная со своими вторыми производными в области G и удовлетворяющая в G Лапласа уравнению =0. Г. ф. возникают при решении задач электростатики, теории тяготения, гидродинамики несжимаемой жидкости, теории упругости и др. Г. ф.… … Физическая энциклопедия
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ — уравнение вида где F заданная действительная функция точки х=(xt, ..., х п )области Dевклидова пространства Е п, и действительных переменных (и(х) неизвестная функция) с неотрицательными целочисленными индексами i1 ,..., in, k=0, ..., т, по… … Математическая энциклопедия
 , в каждой точке границы Г к-рой существует нормаль, задано эллиптич. уравнение 2-го порядка
, в каждой точке границы Г к-рой существует нормаль, задано эллиптич. уравнение 2-го порядка 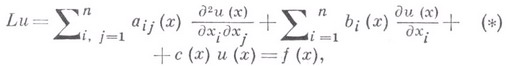
 В. к. з. для уравнения (*) в области
В. к. з. для уравнения (*) в области  наз. следующая задача: из множества всех решений уравнения (*) требуется выделить те, к-рые в каждой граничной точке имеют производные по внутренней конормали N и удовлетворяют условию
наз. следующая задача: из множества всех решений уравнения (*) требуется выделить те, к-рые в каждой граничной точке имеют производные по внутренней конормали N и удовлетворяют условию 
