ПОЛОЖИТЕЛЬНЫЙ ФУНКЦИОНАЛ

ПОЛОЖИТЕЛЬНЫЙ ФУНКЦИОНАЛ

на алгебре с инволюцией * - линейный функционал f на * - алгебре А, удовлетворяющий условию для всех 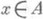. Важность П. ф. и причина их введения заключается, в частности, в том, что они используются в так наз. ГНС-конструкции - одного из основных методов исследования структуры банаховых * - алгебр. На ней (и на ее обобщениях, напр. на веса на С*-алгебрах) основано доказательство теоремы - абстрактной характеризации равномерно замкнутых * - алгебр операторов в гильбертовом пространстве и теоремы о полноте системы неприводимых унитарных представлений локально, компактной группы.

ГНС-конструкция есть способ построения по произвольному П. ф. f на * -алгебре Ас единицей такого * - представления pf алгебры Ав гильбертовом пространстве Hf, что f(x)=<pf(x) x, x> для всех , где - нек-рый циклич. вектор, к-рый состоит в следующем. В Аопределяется полускалярное произведение <x, y>=f(y*x);соответствующим нейтральным подпространством является левый идеал Nf={x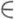А:f(x*x)=0}, поэтому в предгильбертовом пространстве A/Nf корректно определены операторы левого умножения L а на элементы ;

операторы La непрерывны и продолжаются до непрерывных операторов 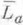в пополнении Hf пространства A/Hf. Отображение яу, переводящее в , и есть требуемое, представление, причем в качестве x можно взять образ единицы при суперпозиции канонич. отображений .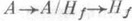

Лит.:[1] Гельфанд И. М., Наймарк М. А., "Изв. АН СССР. Сер. матем.", 1948, т. 12, с. 445-80; [2] S еg al I., "Bull. Amer. Math. Soc.", 1947, v. 53; [3] Наймарк М. А., Нормированные кольца, 2 изд., М., 1968. В. С. Шульман.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужен реферат?

Полезное


Смотреть что такое "ПОЛОЖИТЕЛЬНЫЙ ФУНКЦИОНАЛ" в других словарях:

  • ХАРАКТЕРИСТИЧЕСКИЙ ФУНКЦИОНАЛ — аналог понятия характеристической функции, используемый в бесконечномерном случае. Пусть непустое множество, Г векторное пространство определенных на действительных функций, наименьшая алгебра подмножеств относительно к рой измеримы все функции… …   Математическая энциклопедия

  • СИММЕТРИЧНАЯ АЛГЕБРА — алгебра Енад полем комплексных чисел, снабженная инволюцией . Примерами С. а. являются: алгебра непрерывных функций на компакте, в к рой инволюция определяется как переход к комплексно сопряженной функции; алгебра ограниченных линейных операторов …   Математическая энциклопедия

  • ИНВАРИАНТНОЕ ИНТЕГРИРОВАНИЕ — на группе интегрирование функций на топологич. группе, обладающее нек рым определенным свойством инвариантности относительно групповых операций. А именно, пусть G локально компактная топологич. группа, C0(G) векторное пространство всех… …   Математическая энциклопедия

  • Однородная функция — степени   числовая функция такая, что для любого и выполняется равенство: причём называют порядком однородности. Различают также положительно однородные функции, для которых равенство …   Википедия

  • ПОЛЯРНОЕ РАЗЛОЖЕНИЕ — 1) П. р. линейного преобразования разложение линейного преобразования конечномерного евклидова (или унитарного) пространства Lв произведение самосопряженного и ортогонального (соответственно унитарного) преобразования. Каждое линейное… …   Математическая энциклопедия

  • ПОЛУУПОРЯДОЧЕННОЕ ПРОСТРАНСТВО — общее название векторных пространств, в к рых определено бинарное отношение частичного порядка, согласованное определенным образом с векторной структурой пространства. Введение порядка в функциональных пространствах позволяет исследовать в общих… …   Математическая энциклопедия

  • БАНАХОВА РЕШЕТКА — банахова структура, векторная решетка (структура), являющаяся одновременно банаховым пространством с нормой, удовлетворяющей условию монотонности: Б. р. наз. также линеалом, а произвольную нормированную, т. е. векторную решетку с монотонной… …   Математическая энциклопедия

  • ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ — уравнение вида где F заданная действительная функция точки х=(xt, ..., х п )области Dевклидова пространства Е п, и действительных переменных (и(х) неизвестная функция) с неотрицательными целочисленными индексами i1 ,..., in, k=0, ..., т, по… …   Математическая энциклопедия

  • Супермодулярность — Супермодулярность  обобщение свойства выпуклости функций числового аргумента на функционалы, определённые на множествах произвольной природы. Функционал v, определённый на подмножествах множества N, называется супермодулярным, если для любых …   Википедия

  • Модулярность — Супермодулярность  обобщение свойства выпуклости функций числового аргумента на функционалы, определенные на множествах произвольной природы. Функционал v, определенный на подмножествах множества N, называется супермодулярным, если для любых… …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»