БАНАХОВА РЕШЕТКА

банахова структура,-векторная решетка (структура), являющаяся одновременно банаховым пространством с нормой, удовлетворяющей условию монотонности:

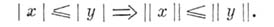
Б. р. наз. также 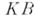-линеалом, а произвольную нормированную, т. е. векторную решетку с монотонной нормой - 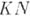- линеалом. При пополнении нормированной решетки по норме порядковые отношения могут быть распространены на получающееся банахово пространство так, что оно оказывается Б. р. Если в решетке можно ввести банахову топологию, превращающую ее в Б. р., то такая топология единственна. Простейший пример Б. р.- пространство 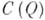непрерывных функций на произвольном компактном топологич. пространстве 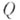с естественным упорядочением и с обычной (равномерной) нормой. Другие примеры Б. р.- пространства 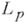, пространства Орлича. В Б. р. сходимость по норме есть 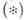- сходимость для сходимости с регулятором. В нормированной решетке это не так.

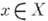Важный частный случай - Б. р. ограниченных элементов. Если в решетке Xимеется сильная единица , т. е. для каждого существует такое 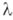, что 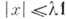, то наименьшее 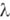, для к-рого это неравенство справедливо, принимается за 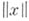. Полученная нормированная решетка наз. нормированной решеткой ограниченных элементов; если же она полна по норме, то она наз. <Б. <р. ограниченных элементов. В Б. р. (и даже в нормированной решетке) ограниченных элементов сходимость по норме совпадает со сходимостью с регулятором, а ограниченность множества элементов по норме совпадает с ограниченностью по упорядочению. Если нормированная решетка ограниченных элементов есть условно а-полная решетка, то она полна по норме.

Пространство 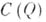есть Б. р. ограниченных элементов, в к-роп за единицу принята функция 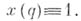Для всякой Б. р. X ограниченных элементов существует такое компактное хаусдорфово пространство Q, что Xалгебраически и структурно изоморфна пространству 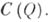Это - абстрактная характеристика Б. р. непрерывных функций на компактном хаусдорфовом пространстве.

В любой нормированной решетке каждый аддитивный и непрерывный по норме функционал регулярен и, более того, представим в виде разности двух аддитивных и непрерывных по норме положительных функционалов. В Б. р. всякий положительный аддитивный функционал непрерывен по норме, и значит классы регулярных и аддитивных непрерывных по норме функционалов совпадают. Пространство X' , сопряженное в банаховом смысле к нормированной решетке X, есть условно полная Б. р. В нормированной решетке теорема Хана - Банаха допускает следующее уточнение: для любого 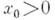существует такой положительный аддитивный непрерывный по норме функционал f , что f(x₀)=||x₀||, ||f||=1.

Лит.:[1] Вулих Б. 3., Введение в теорию полуупорядоченных пространств, М., 1961; [2] Дэй М. М., Нормированные линейные пространства, пер. с англ., М., 1961. Б. 3. Вулих.